Файл: Конспект лекций (часть 1) Составители А. М. Коленченко Е. Н. Коленченко саранск.docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 09.11.2023

Просмотров: 421

Скачиваний: 4

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

СОДЕРЖАНИЕ

УДК 621.3

БИБЛИОГРАФИЧЕСКИЙ СПИСОК 97

ВВЕДЕНИЕ

Понятие о линейных и нелинейных элементах и цепях

Индуктивность

Основные определения, относящиеся к топологии электрической цепи

Режимы работы электрической цепи

АНАЛИЗ И РАСЧЕТ СЛОЖНЫХ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ ПОСТОЯННОГО ТОКА

Метод узловых потенциалов

Метод двух узлов

Метод эквивалентного генератора

Баланс мощности

АНАЛИЗ И РАСЧЕТ ПРОСТЕЙШИХ ЦЕПЕЙ ПОСТОЯННОГО ТОКА С НЕЛИНЕЙНЫМИ ЭЛЕМЕНТАМИ

ЭЛЕКТРИЧЕСКИЕ ЦЕПИ СИНУСОИДАЛЬНОГО ТОКА

Получение синусоидальной ЭДС

Представление синусоидальных величин комплексными числами

Некоторые операции с комплексными числами

Изображение производной синусоидальной функции

Метод комплексных амплитуд (символический метод). Законы Кирхгофа для синусоидальных цепей

Законы Ома и Кирхгофа для синусоидальных цепей

Индуктивность в цепи синусоидального тока

Конденсатор в цепи синусоидального тока

Комплексная мощность Если известны напряжение и ток в цепи переменного тока, имеющие комплексные выраженияU  Um 2 ejψuи I Im ejψi, а также сдвиг фаз между ними φψuψi, то выражение полной комплексной мощности в данной цепиопределяется как произведение комплекса напряжения на сопряженный комплекс тока и имеет вид: S  U  I*  U ejψu I e jψi U I ej(ψuψi)  S U I ejφ U I cosφ jU I sinφ P j Q, гдеP ReU  I* , а Q ImU  I* ; – полная мощность ВА; P– активная мощность, измеряется в Вт, кВт, МВт; Q– реактивная мощность, измеряется в вольт-амперах реактивных ВАр, кВАр, МВАр. Рис. 5.23Треугольник мощностей на комплексной плоскости показан на рис. 5.23.Этот случай соответствует положительному значению реактивной мощности Q . 1   ...   23   24   25   26   27   28   29   30   ...   56

Последовательное и параллельное соединения элементов R, L, C. Резонансы напряжений и токов

и UТреугольник сопротивлений

Треугольник проводимостей

Параллельное соединение.

Смешанное соединение.

ЭЛЕКТРИЧЕСКИЕ ЦЕПИ СО ВЗАИМНОЙ ИНДУКТИВНОСТЬЮ ПОД ВОЗДЕЙСТВИЕМ СИНУСОИДАЛЬНОГО НАПРЯЖЕНИЯ

Последовательное соединение индуктивно связанных катушек при согласном и встречном включении

Входное сопротивление воздушного трансформатора

ТРЕХФАЗНЫЕ ЦЕПИ

7,1. Основные понятия. Способы изображения симметричной трехфазной

Соединение фаз трехфазного источника питания звездой и

Трехфазные цепи с симметричными пассивными приемниками

Соединение треугольником

Трехфазные цепи с несимметричными пассивными приемниками

Трехфазная цепь с несимметричными пассивными приемниками, включенными треугольником

Мощность в трехфазной цепи

ПЕРЕХОДНЫЕ ПРОЦЕССЫ В ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ

8.1 Основные понятия

Короткое замыкание RL цепи постоянного тока

Отключение цепи RL от источника постоянного напряжения

8.3.2 Короткое замыкание цепи RC (разряд конденсатора С на сопротивлении R )

8.3.3. Релаксационный генератор

МАГНИТНЫЕ ЦЕПИ

Расчет неразветвленной магнитной цепи

Обратная задача.

Катушка индуктивности с ферромагнитным сердечником У катушки без сердечника магнитный потокФ B Sпропорционален магнитной движущей силеF I w, а зависимость Ф(I)является линейной. При наличии магнитопровода магнитный поток катушки (дросселя) значительно возрастает при прочих равных условиях, т.к. он создается не только катушкой с током (источником внешнего магнитного поля), но и соответствующим ферромагнитным веществом магнитопровода (источником внутреннего магнитного поля).Известно, Ф B S μ H S, т.е. Ф μ, а для ферромагнитных материалов на несколько порядков выше магнитной проницаемости воздухаμ0 . Значит, одинаковый магнитный поток в катушке с магнитопроводом можно получить призначительно меньшей намагничивающей силе F I  w.Схема замещения реальной катушки индуктивности имеет вид рис.9.12. Здесь i0Рис.9.12 Рис.9.13 ток катушки; R- активное сопротивление проводов катушки; x ω L индуктивное сопротивление катушки; R0 - активное сопротивление, обусловленное потерями мощности в катушкеR PM;0 I2x0 - индуктивное сопротивление, обусловленное основным магнитным потоком. По второму закону КирхгофаU  R I jx I E . 0 0Векторная диаграмма, построенная в соответствии с данным уравнением, имеет вид (рис.10.13). Так какe  dФ, то Ф отстает по фазе от E наdtπ. Кроме того,2 0Ф отстает по фазе от тока I на угол δвследствие явления гистерезиса. Так как зависимостьB(H)– нелинейная, следовательно нелинейной будет и зависимость Ф(i0 ) (рис.9.14). Так как напряжение зависимость Ф(t) .u(t)Рис.9.14синусоидальное, значит синусоидальной будет и Но из-за нелинейностиB(H)ток катушки с сердечникомi0 (t)будет несинусоидальным (см. рис.9.14), а это значит, что нелинейная индуктивность является генератором высших гармоник тока. Из рис. 9.14 видно, что ток i0опережает по фазе поток Фна гистерезисный угол δ(ток достигает нуля раньше магнитного потока).Для катушки индуктивности с магнитопроводом, имеющим воздушный зазор (рис.9.15), по закону ОмаФ F,Rм гдеRмопределяются, в основном, сопротивлением воздушного зазора. Рис. 9.15 Рис.9.16 Увеличение воздушного зазора увеличиваетRм, а значит должно уменьшить поток Ф. Но этого не происходит, т.к. из формулыU 4,44  f w Фmследует, что ФmU4,44  f w, т.е. величина потока зависит только от действительного значения питающего напряжения, которое, естественно, не меняется. Значит, не меняется и поток. Это объясняется тем, что при увеличении δувеличивается намагничивающая силаI wдо значения, при котором поток Ф(а значит и отношениеF) остаетсяRм постоянным. Ток дросселя увеличивается за счет того, что уменьшается полное сопротивление катушки вследствие уменьшения ее реактивного сопротивления (из- за уменьшения индуктивности) (см. рис.9.16).Таким образом, путем изменения величины воздушного зазора в магнитопроводе, можно регулировать ток катушки индуктивности (дросселя) при включении ее в цепь переменного тока при неизменности питающего напряжения. В данном случае, катушка индуктивности с ферромагнитным сердечником, в цепи которого имеется регулируемый воздушный зазор, выполняет функции регулируемого сопротивления. БИБЛИОГРАФИЧЕСКИЙ СПИСОК Башарин С.А., Федоров В.В. Теоретические основы электротехники. Учебное пособие. М.: ACADEMA. 2004. – 304с. Иванов И.И., Соловьев Г.И., Равдоник В.С. Электротехника. Учебник. 3-е изд., стер. – СПб.: Издательство «Лань», 2005. – 496с., ил. Касаткин А.С., Немцов М.В. Основы электротехники для студентов вузов. – М.: Энергоатомиздат, 2000. 1   ...   48   49   50   51   52   53   54   55   56

Параллельное соединение.


В общем случае пусть имеем цепь, изображенную на рис.5.45.


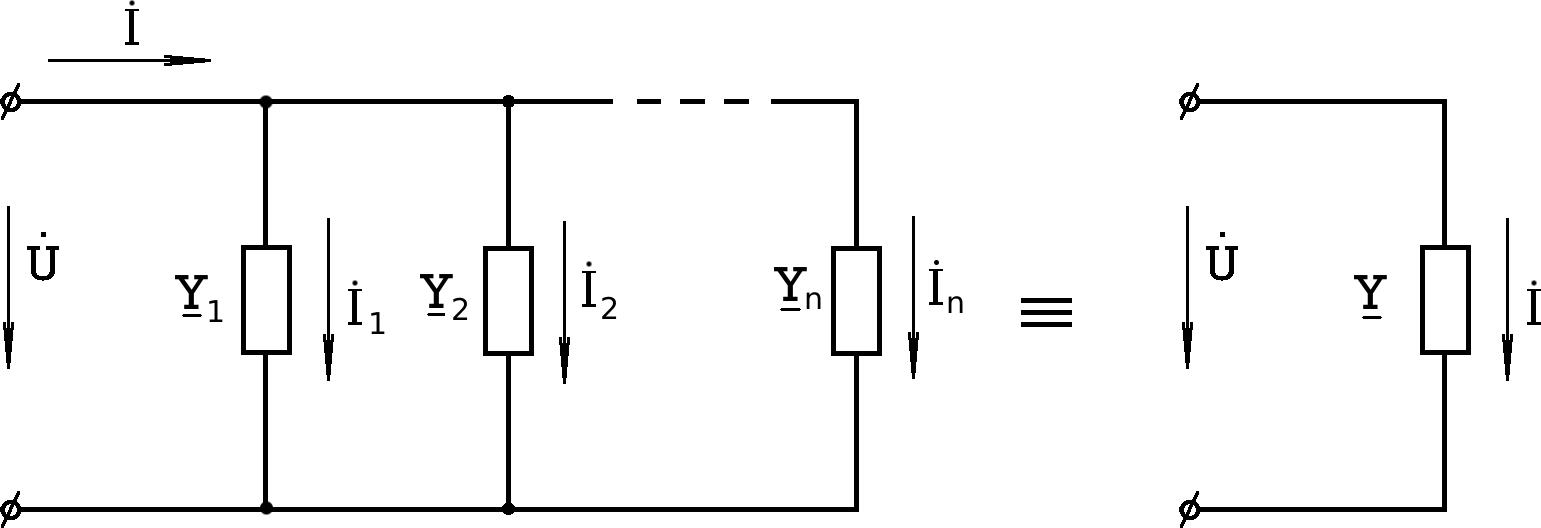
Рис.5.45


По I закону Кирхгофа имеем:


1
I I

2
I
I

n


I
n
.


k

k1


n

Распишем компоненты данного уравнения:

U Y U Y1 U Y2 U Yn U Yk.

k1

Поделим обе части на U , получим



Y Yk.

k1

Сумма комплексных проводимостей всех параллельно соединенных ветвей

n

Y Ykk1

называется эквивалентнойкомплекснойпроводимостью.

Рассмотрим два примера параллельного соединения элементов: RL (рис.5.46) и RC (рис.5.47).

1)




Здесь 2)

n




g gk,

k1

n




C Ck.

k1

Рис.5.46




Здесь

g g,

1 n1 .

Рис.5.47


n
kLL

k1

k1 k

Общий ток для данного случая
1   ...   28   29   30   31   32   33   34   35   ...   56

Смешанное соединение.


I U Y.

В общем случае пусть имеем цепь вида (рис.5.48)




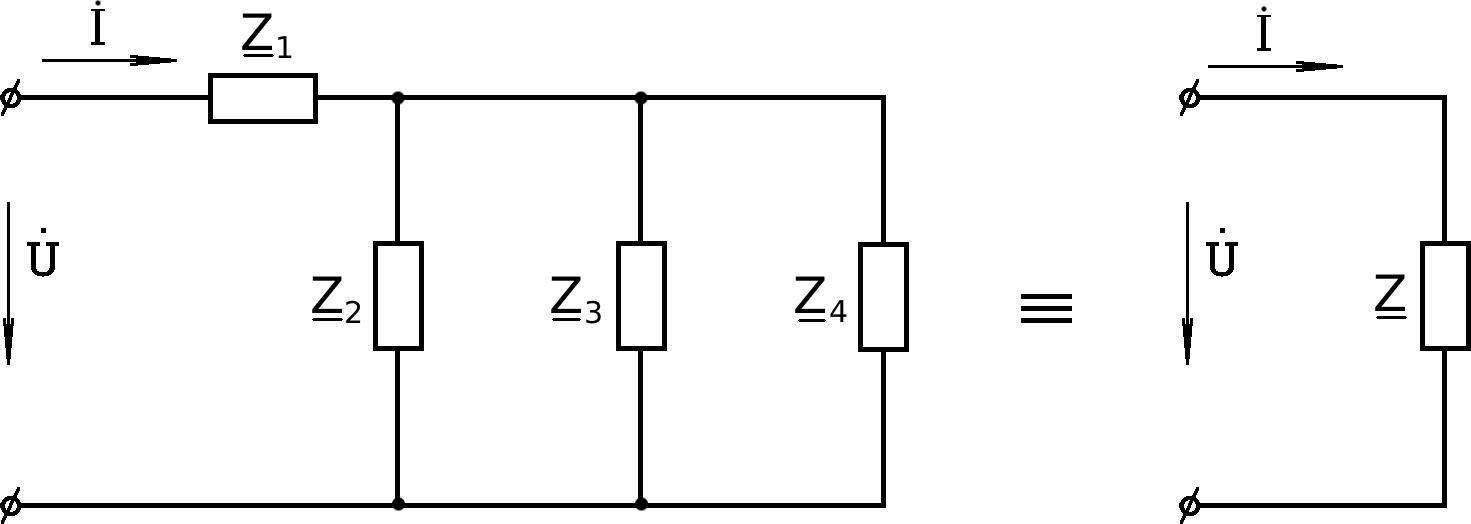
Здесь
Z ZZ

Рис.5.48

, где, в свою очередь, Z

1 , Y

1 1 1 .



1 экв

эквY
экв

экв

2




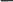
Z
Z3 Z4



        1. Эквивалентные участки цепи с последовательным и параллельным соединениями



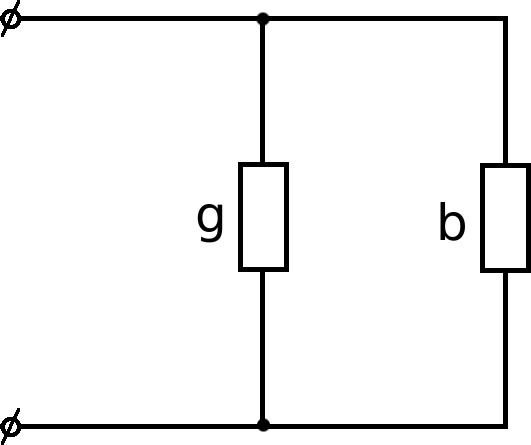Пусть имеем цепь вида (рис.5.49). Требуется перейти к цепи вида (рис.5.50).


Рис.5.49 Рис.5.50



Для цепи на рис.5.49 комплексное сопротивление равно Для цепи на рис.5.50 имеем:

Z R

j x.


Yg

j b 1 1



R j x

R j x

R j x.



Z R j x

(R

j x) (R

j x)

R2 x2

R2 x2 R2 x2

Следовательно,

g R,

R2 x2

b x.

R2 x2

Обратная задача, т.е. задача перехода от цепи на рис.5.50 к цепи, изображенной на рис.5.49, решается следующим образом:

Z 1 1

1 (g j b)

g j b

R

j x.

Y g j b

(g j b) (g

j b)

g2 b2 g2 b2


Следовательно,

R g,

g2 b2

x b.

b2 g2



    1. 1   ...   29   30   31   32   33   34   35   36   ...   56

ЭЛЕКТРИЧЕСКИЕ ЦЕПИ СО ВЗАИМНОЙ ИНДУКТИВНОСТЬЮ ПОД ВОЗДЕЙСТВИЕМ СИНУСОИДАЛЬНОГО НАПРЯЖЕНИЯ




      1. Понятие взаимной индуктивности







Рис.6.1

Цепи со взаимной индуктивностью находят широкое применение на практике: рис.6.1 – трансформатор, см. рис.5.32 – входная цепь приемника.

Сущность взаимоиндукции заключается в том, что изменение тока в одном элементе цепи приводит к изменению ЭДС в другом элементе другой цепи.

Такие элементы и цепи называются индуктивно связанными, а явление называется взаимоиндукцией.

При составлении уравнений для индуктивно связанных цепей необходимо знать, согласно или встречно направлены потоки самоиндукции и взаимоиндукции и соответствующие им ЭДС. Это можно узнать, если известно направление намотки катушек на сердечнике и выбрано положительное направление токов в них. Однако это сложно изобразить графически. Вместо этого удобнее показывать их одноименные зажимы (начала катушек).

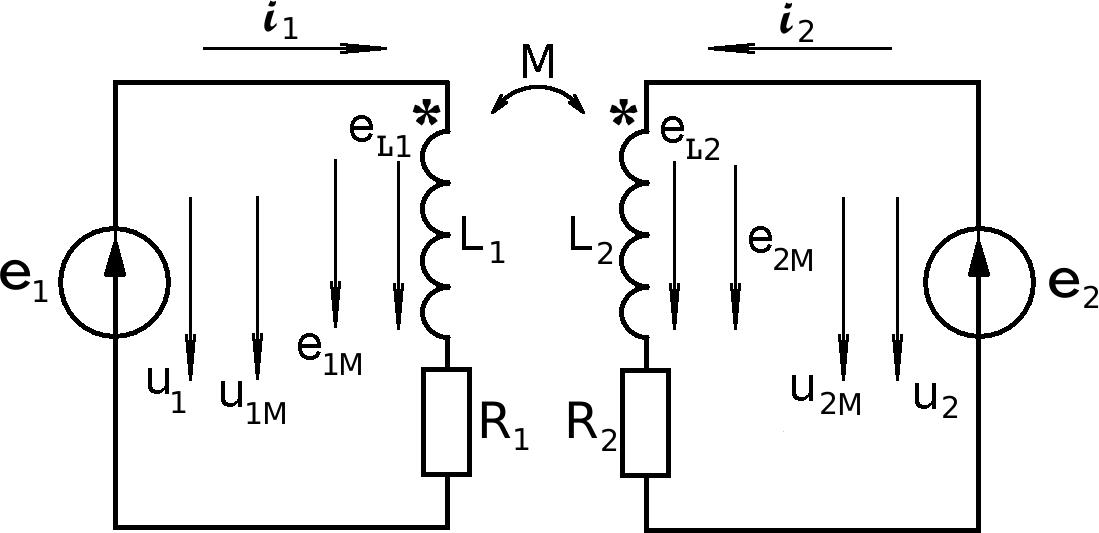Для одноименных зажимов индуктивно связанных катушек характерно то, что при одинаковом

направлении токов i1 и i2


Рис.6.2

относительно этих зажимов магнитные потоки самоиндукции и

взаимоиндукции и соответствующие им ЭДС складываются (рис.6.2). Такое включение катушек называется согласным.


Рис.6.3



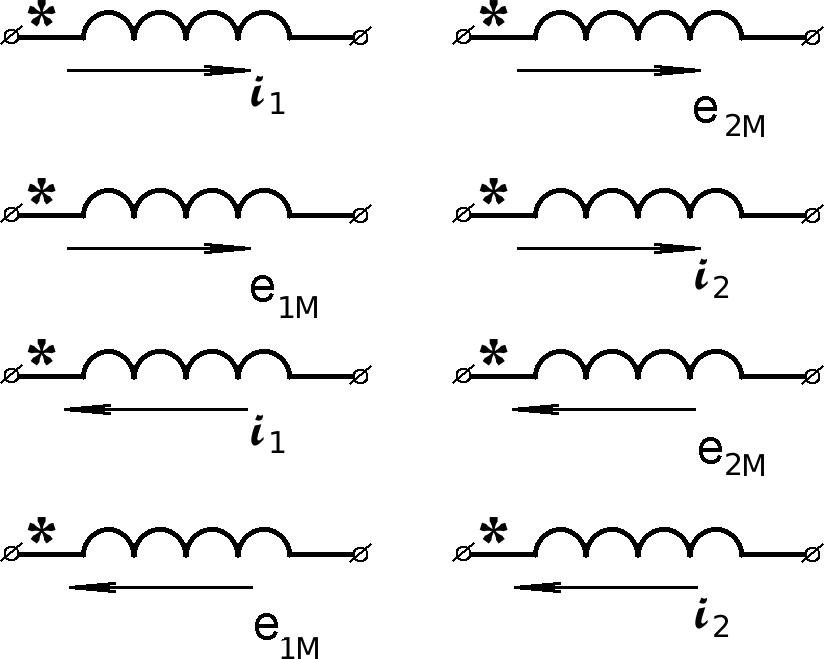
Рис.6.4

При встречномвключении (см. рис.6.3) токи катушек неодинаково ориентированны относительно одноименных зажимов, следовательно, и магнитные потоки самоиндукции и взаимоиндукции встречно включенных катушек противоположны; навстречу друг другу будут действовать и

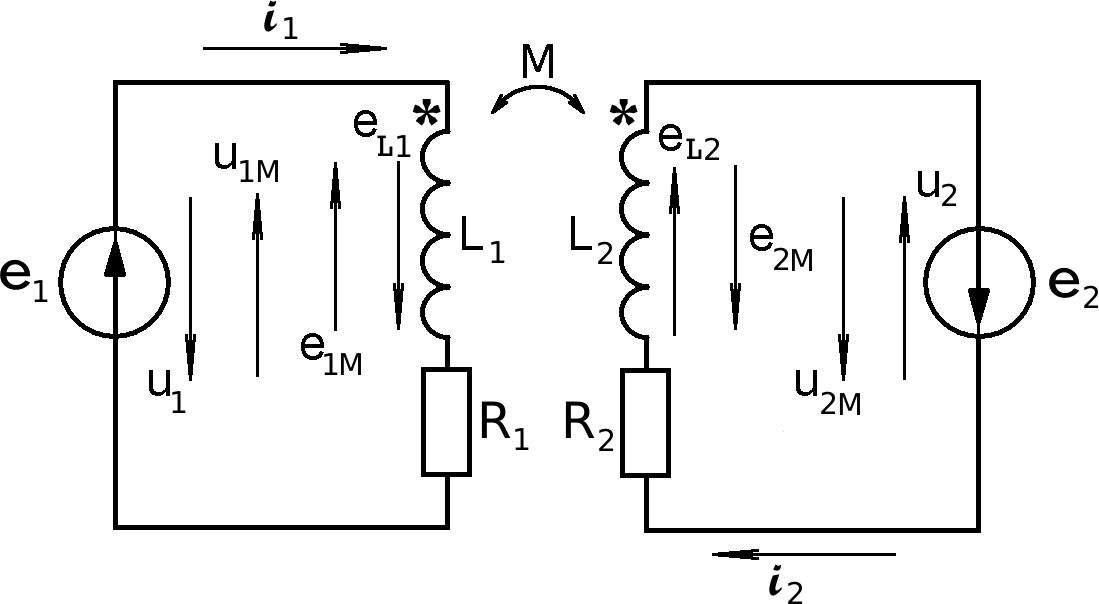соответствующие им ЭДС.

При изображении токов и ЭДС взаимной индукции, вызываемых этими токами, используют правило: токи и наведенные ими ЭДС взаимной индукции одинаковоориентированны относительно одноименных зажимов.

На рис.6.4 это правило проиллюстрировано графически.

ЭДС взаимной индукции для катушки с сердечником при согласном включении определяются по формуле:

Смотрите также файлы