Файл: Конспект лекций (часть 1) Составители А. М. Коленченко Е. Н. Коленченко саранск.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.11.2023
Просмотров: 434
Скачиваний: 4
СОДЕРЖАНИЕ
Понятие о линейных и нелинейных элементах и цепях
Основные определения, относящиеся к топологии электрической цепи
Режимы работы электрической цепи
АНАЛИЗ И РАСЧЕТ СЛОЖНЫХ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ ПОСТОЯННОГО ТОКА
Метод эквивалентного генератора
АНАЛИЗ И РАСЧЕТ ПРОСТЕЙШИХ ЦЕПЕЙ ПОСТОЯННОГО ТОКА С НЕЛИНЕЙНЫМИ ЭЛЕМЕНТАМИ
ЭЛЕКТРИЧЕСКИЕ ЦЕПИ СИНУСОИДАЛЬНОГО ТОКА
Представление синусоидальных величин комплексными числами
Некоторые операции с комплексными числами
Изображение производной синусоидальной функции
Метод комплексных амплитуд (символический метод). Законы Кирхгофа для синусоидальных цепей
Законы Ома и Кирхгофа для синусоидальных цепей
Индуктивность в цепи синусоидального тока
Конденсатор в цепи синусоидального тока
Последовательное и параллельное соединения элементов R, L, C. Резонансы напряжений и токов
ЭЛЕКТРИЧЕСКИЕ ЦЕПИ СО ВЗАИМНОЙ ИНДУКТИВНОСТЬЮ ПОД ВОЗДЕЙСТВИЕМ СИНУСОИДАЛЬНОГО НАПРЯЖЕНИЯ
Последовательное соединение индуктивно связанных катушек при согласном и встречном включении
Входное сопротивление воздушного трансформатора
7,1. Основные понятия. Способы изображения симметричной трехфазной
Соединение фаз трехфазного источника питания звездой и
Трехфазные цепи с симметричными пассивными приемниками
Трехфазные цепи с несимметричными пассивными приемниками
Трехфазная цепь с несимметричными пассивными приемниками, включенными треугольником
ПЕРЕХОДНЫЕ ПРОЦЕССЫ В ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ
Короткое замыкание RL цепи постоянного тока
Отключение цепи RL от источника постоянного напряжения
8.3.2 Короткое замыкание цепи RC (разряд конденсатора С на сопротивлении R )
8.3.3. Релаксационный генератор
записываемого по виду уравнения (8.12):
L p2 R p 1
C
0 .
Это уравнение также можно получить, записав его по виду комплексного
сопротивления
Zвх
относительно входных зажимов:
Zвх
R
j ω L
1 0
j ω C
или
R j ω C ( j ω) 2 L C 1
j ω C
0 . (8.14)
Умножим на
jω C
левую и правую части выражения (8.14)
( jω)2 L C ( jω)R C1 0 .
Разделим на Cи заменим ( jω) на p:
L p2 R p 1
C
0 .
 Решением этого уравнения являются корни:
Решением этого уравнения являются корни: R
Rp1, 2
2 L
δ
δ
ωсв
, (8.15)
где
δ R
-
L
-
коэффициент затухания;
ω 1
-
резонансная частота;
0
 ωcв
ωcв – угловая частота свободных колебаний в контуре.
 Постоянные интегрирования найдем из совместного решения следующих
Постоянные интегрирования найдем из совместного решения следующихуравнений, найденных с помощью законов коммутации.
Известно
i|t0 0 . Тогда из (8.13) получим первое уравнение:
0 A1 A2
(8.16)
Для получения второго уравнения выполним следующие операции.
Продифференцируем обе части уравнения (8.13), получим:
di A p
ep1t A p
ep2 t.
Очевидно:
dt1
di
1 2 2
A p A p
(8.17)
dt
1 1 2 2
t0
Далее, подставим начальные условия в уравнение (8.10)
L
di
dt
0 R U E
и выразим производную
t0
di
dt
E U. (8.18)
L
t0
Сравнивая (8.17) и (8.18) получим второе уравнение для определения постоянных интегрирования и запишем систему уравнений
A p
A p
E U;
1 1 2 2
L
(8.19)
0 A1 A2 .
Найдем постоянные интегрирования из решения системы (8.19).
Выразим из второго уравнения
A2 A1
и подставим в первое
A1 p1
A1
p2
E U.
L
Таким образом, постоянные интегрирования будут равны:
E U
-
1
L
E U
E U
A. (8.20)
p1 p2
L (δ γ δ γ)
2 L γ 2
Подставим найденные значения
p1 и
p2 ,
A1 и A2
в уравнение (8.13), получим
i E U
2 L γ
e(δγ)t
E U
2 L γ
e(δγ)t. (8.21)
 В зависимости от величины γ , а именно, от соотношения между
В зависимости от величины γ , а именно, от соотношения междусобой δ2
и ω2
R2
(
и
1 ), процесс изменения тока в R, L, C цепи может быть
0 2 L
L C
апериодическимлибо колебательным.
Апериодический процесс
0
Данный процесс наблюдается при δ2 ω2 , в результате чего корни уравнения
p1,2
есть вещественные отрицательные числа
p1 δ γ
и p2 δ γ, показанные на
комплексной плоскости на рис.8.15.
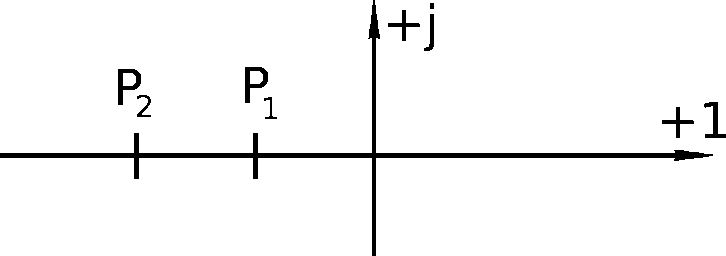
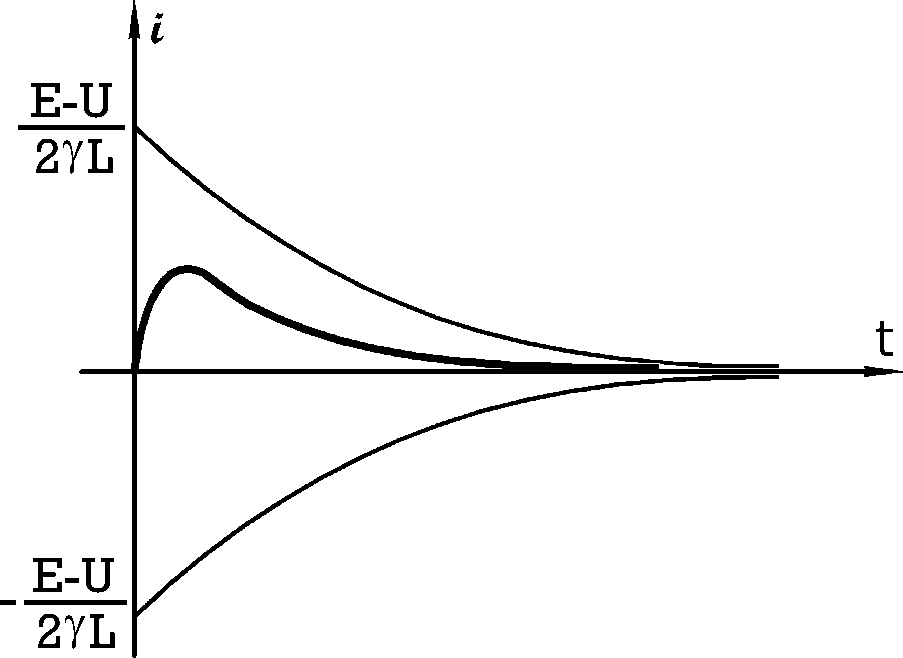 Рис.8.15
Рис.8.15Рис.8.16
В этом случае ток iописывается уравнением (8.21), а график процесса изображен на рис.8.16.
-
Колебательный процесс
При соотношении
δ2 ω2
наблюдается колебательный процесс изменения
0
тока в цепи. В этом случае корни
p1,2
являются комплексными сопряженными
числами
p1 δ j ωсви
p2 δ j ωсв , где
ωсв
– собственная частота свободных
колебаний (Tсв
2 π
ω
– период свободных колебаний). Они располагаются
св
симметрично относительно действительной оси в левой полуплоскости, на полуокружности, центр которой совпадает с началом координат, а радиус равен
1
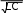 ω0
ω0 (рис.8.17).
В этом случае постоянные интегрирования
A1 и
A2 находятся также из