Файл: Конспект лекций (часть 1) Составители А. М. Коленченко Е. Н. Коленченко саранск.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.11.2023
Просмотров: 425
Скачиваний: 4
СОДЕРЖАНИЕ
Понятие о линейных и нелинейных элементах и цепях
Основные определения, относящиеся к топологии электрической цепи
Режимы работы электрической цепи
АНАЛИЗ И РАСЧЕТ СЛОЖНЫХ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ ПОСТОЯННОГО ТОКА
Метод эквивалентного генератора
АНАЛИЗ И РАСЧЕТ ПРОСТЕЙШИХ ЦЕПЕЙ ПОСТОЯННОГО ТОКА С НЕЛИНЕЙНЫМИ ЭЛЕМЕНТАМИ
ЭЛЕКТРИЧЕСКИЕ ЦЕПИ СИНУСОИДАЛЬНОГО ТОКА
Представление синусоидальных величин комплексными числами
Некоторые операции с комплексными числами
Изображение производной синусоидальной функции
Метод комплексных амплитуд (символический метод). Законы Кирхгофа для синусоидальных цепей
Законы Ома и Кирхгофа для синусоидальных цепей
Индуктивность в цепи синусоидального тока
Конденсатор в цепи синусоидального тока
Последовательное и параллельное соединения элементов R, L, C. Резонансы напряжений и токов
ЭЛЕКТРИЧЕСКИЕ ЦЕПИ СО ВЗАИМНОЙ ИНДУКТИВНОСТЬЮ ПОД ВОЗДЕЙСТВИЕМ СИНУСОИДАЛЬНОГО НАПРЯЖЕНИЯ
Последовательное соединение индуктивно связанных катушек при согласном и встречном включении
Входное сопротивление воздушного трансформатора
7,1. Основные понятия. Способы изображения симметричной трехфазной
Соединение фаз трехфазного источника питания звездой и
Трехфазные цепи с симметричными пассивными приемниками
Трехфазные цепи с несимметричными пассивными приемниками
Трехфазная цепь с несимметричными пассивными приемниками, включенными треугольником
ПЕРЕХОДНЫЕ ПРОЦЕССЫ В ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ
Короткое замыкание RL цепи постоянного тока
Отключение цепи RL от источника постоянного напряжения
8.3.2 Короткое замыкание цепи RC (разряд конденсатора С на сопротивлении R )
8.3.3. Релаксационный генератор
i CduC
U
1 C e
t
U
RC
t
eτ.
dt R C R
Рис.8.9
Временная диаграмма данного процесса
изображена на рис.8.9.
8.3.2 Короткое замыкание цепи RC (разряд конденсатора С на сопротивлении R )
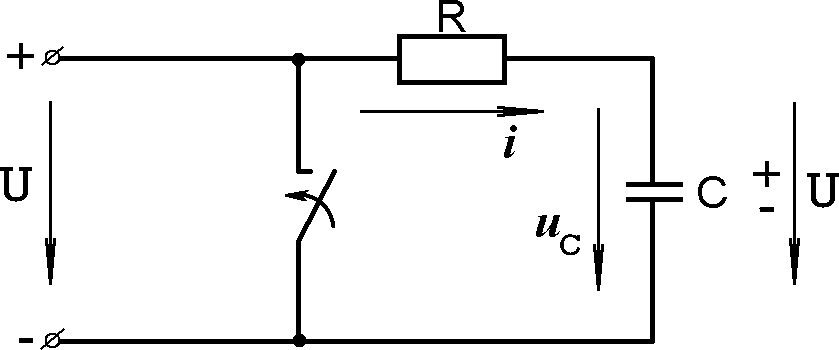 До коммутации конденсатор был заряжен до входного напряжения U,
До коммутации конденсатор был заряжен до входного напряжения U,потому
uC|t0 U.
После замыкания ключа по цепи RC (рис.8.10) будет протекать ток
Рис.8.10
i CduC.
dt
Ток будет существовать до тех пор, пока энергия электрического поля
CU2
WЭ 2 не преобразуется в тепло в сопротивлении R.
C
По второму закону Кирхгофа имеем i R u 0 , или
R CduC
dt
-
uC
0 . (8.9)
Так как конденсатор за время
t
разрядится полностью, то
uCпр|t 0 .
Поэтому в любой момент переходного процесса uC uCсв.
Решением уравнения (8.9) является выражение
C C св
u u A ept.
Значение A определяется из условия, задаваемого вторым законом
коммутации
uC|t0 (uCсв uCпр) |t0 uCсв|t0 U.
С другой стороны
p0
u u A e A.
Ct0 Cсве0
Следовательно, A=U. Величина корня рдля RC – цепи была получена выше,
см.(8.8):
p
-
. Окончательно получим:
R C
uC u
Cсв
U e
tRC
t
U eτ.
 Выражение для тока разряда iв этой цепи:
Выражение для тока разряда iв этой цепи:du
1 t
U t
i CC
dt
CU
eτ
R C
eτ.
R
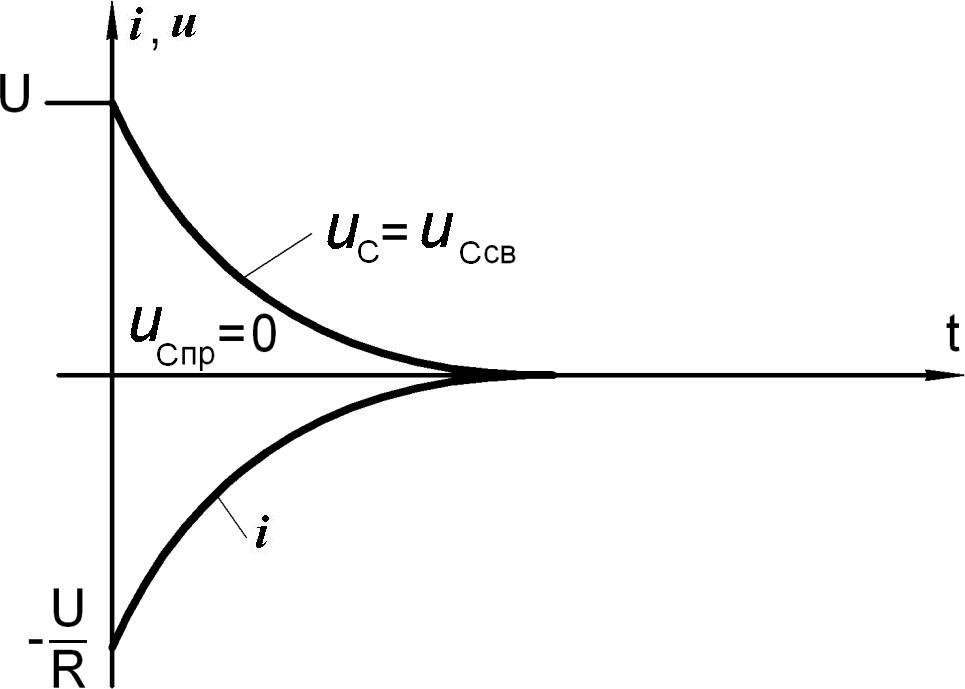
Рис.8.11
Очевидно, чем больше R и C, тем медленнее протекает процесс разряда конденсатора (рис.8.11).
Процессы заряды и разряда конденсатора, рассмотренные в параграфах 8.3.1 и 8.3.2, называются релаксационными.
На основе этих процессов построены релаксационные генераторы, используемые для получения пилообразного напряжения необходимого для работы осциллографов, телевизоров и др.
8.3.3. Релаксационный генератор
Принципиальная схема простейшего релаксационного генератора показана на рис.8.12.
Здесь УЭ – управляющий элемент (неоновая лампа).
Принцип работы генератора заключается в следующем.
1
После замыкания ключа конденсатор медленно заряжается через большое
сопротивление R с постоянной времени
τ R C. При напряжении
uC uзаж
проводимость неоновой лампы резко увеличивается за счет ионизации газа.
2
R
нл
Конденсатор очень быстро разряжается с постоянной времени τ C, где R–
нл
сопротивление неоновой лампы при тлеющем разряде.
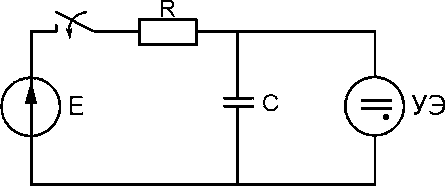
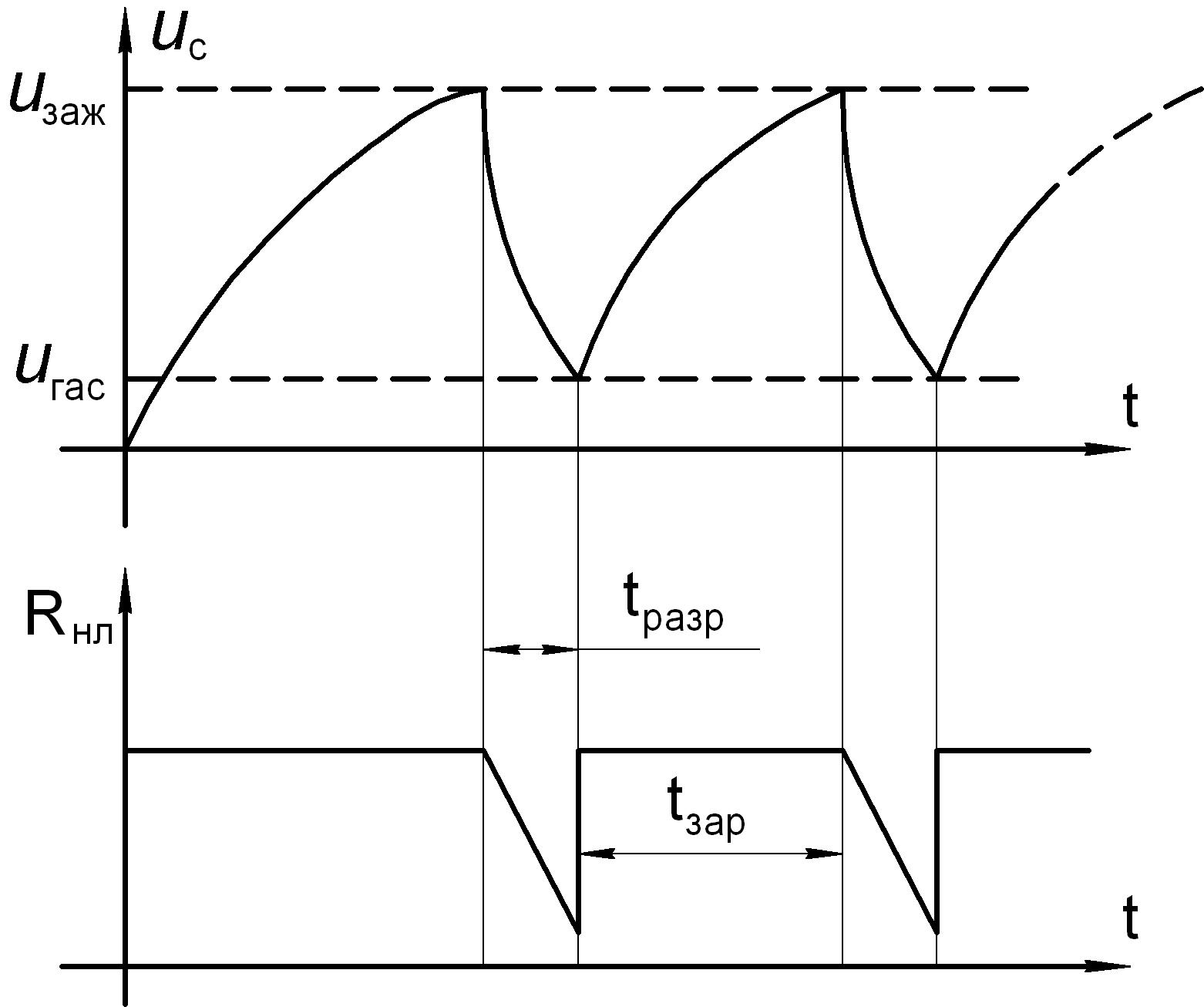 Рис.8.12
Рис.8.12Выбирают
R Rнл, вследствие чего tзар tразр.
Рис.8.13
При уменьшении напряжения на конденсаторе до напряжения
Uгас, разряд в
лампе прекращается, а ее сопротивление резко возрастает. В результате этого снова
начинается заряд конденсатора до
uC uзаж. И т.д.
Если цепь не разомкнуть, то этот процесс будет длиться бесконечно долго (рис.8.13).
-
Переходные процессы в R, L, C цепи. Включение R, L, C цепи на постоянное напряжение (ЭДС)
Пусть начальные условия в цепи (рис.8.14) следующие
uC(0) U;
i(0) 0 , что
означает, что до замыкания ключа емкость была заряжена до напряжения U.
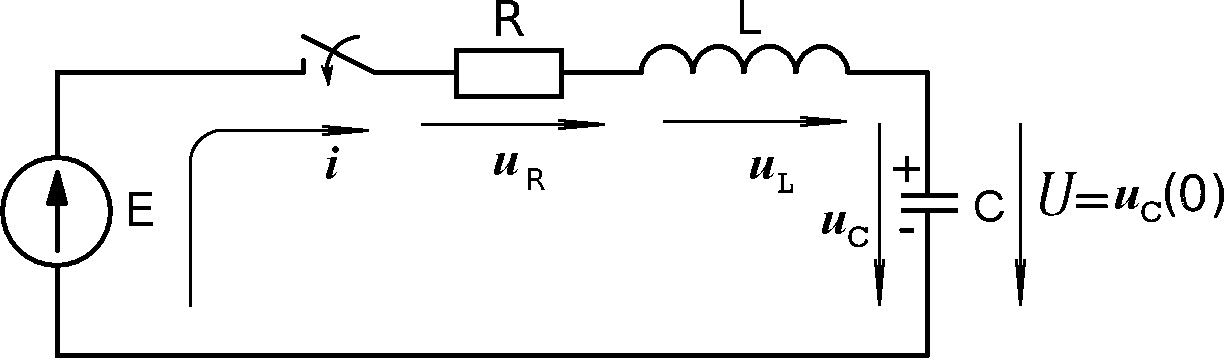
Рис.8.14
Очевидно, что эти параметры после завершения переходного процесса будут равны:
uCпр E; iпр 0 .
Это означает, что конденсатор дозарядится (или разрядится) до входного напряжения Е, после чего ток заряда (разряда) прекратится.
По второму закону Кирхгофа:
uL uR uC E;
L di i R u dtC
E; (8.10)
di1 t
. (8.11)
L i R
dtC
idt E
Продифференцируем обе части уравнения (8.11)
d2idi
LR
1 i 0 . (8.12)
dt2 dtC
Пусть
i iпр iсв. Так как
iпр 0 , значит i iсв.
Решением (8.12) является
i A1
ep1 t A
ep2 t. (8.13)
2
Коэффициенты
p1 и
p2 находятся из характеристического уравнения,