Файл: Конспект лекций (часть 1) Составители А. М. Коленченко Е. Н. Коленченко саранск.docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 09.11.2023

Просмотров: 444

Скачиваний: 4

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

СОДЕРЖАНИЕ

УДК 621.3

БИБЛИОГРАФИЧЕСКИЙ СПИСОК 97

ВВЕДЕНИЕ

Понятие о линейных и нелинейных элементах и цепях

Индуктивность

Основные определения, относящиеся к топологии электрической цепи

Режимы работы электрической цепи

АНАЛИЗ И РАСЧЕТ СЛОЖНЫХ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ ПОСТОЯННОГО ТОКА

Метод узловых потенциалов

Метод двух узлов

Метод эквивалентного генератора

Баланс мощности

АНАЛИЗ И РАСЧЕТ ПРОСТЕЙШИХ ЦЕПЕЙ ПОСТОЯННОГО ТОКА С НЕЛИНЕЙНЫМИ ЭЛЕМЕНТАМИ

ЭЛЕКТРИЧЕСКИЕ ЦЕПИ СИНУСОИДАЛЬНОГО ТОКА

Получение синусоидальной ЭДС

Представление синусоидальных величин комплексными числами

Некоторые операции с комплексными числами

Изображение производной синусоидальной функции

Метод комплексных амплитуд (символический метод). Законы Кирхгофа для синусоидальных цепей

Законы Ома и Кирхгофа для синусоидальных цепей

Индуктивность в цепи синусоидального тока

Конденсатор в цепи синусоидального тока

Комплексная мощность Если известны напряжение и ток в цепи переменного тока, имеющие комплексные выраженияU  Um 2 ejψuи I Im ejψi, а также сдвиг фаз между ними φψuψi, то выражение полной комплексной мощности в данной цепиопределяется как произведение комплекса напряжения на сопряженный комплекс тока и имеет вид: S  U  I*  U ejψu I e jψi U I ej(ψuψi)  S U I ejφ U I cosφ jU I sinφ P j Q, гдеP ReU  I* , а Q ImU  I* ; – полная мощность ВА; P– активная мощность, измеряется в Вт, кВт, МВт; Q– реактивная мощность, измеряется в вольт-амперах реактивных ВАр, кВАр, МВАр. Рис. 5.23Треугольник мощностей на комплексной плоскости показан на рис. 5.23.Этот случай соответствует положительному значению реактивной мощности Q . 1   ...   23   24   25   26   27   28   29   30   ...   56

Последовательное и параллельное соединения элементов R, L, C. Резонансы напряжений и токов

и UТреугольник сопротивлений

Треугольник проводимостей

Параллельное соединение.

Смешанное соединение.

ЭЛЕКТРИЧЕСКИЕ ЦЕПИ СО ВЗАИМНОЙ ИНДУКТИВНОСТЬЮ ПОД ВОЗДЕЙСТВИЕМ СИНУСОИДАЛЬНОГО НАПРЯЖЕНИЯ

Последовательное соединение индуктивно связанных катушек при согласном и встречном включении

Входное сопротивление воздушного трансформатора

ТРЕХФАЗНЫЕ ЦЕПИ

7,1. Основные понятия. Способы изображения симметричной трехфазной

Соединение фаз трехфазного источника питания звездой и

Трехфазные цепи с симметричными пассивными приемниками

Соединение треугольником

Трехфазные цепи с несимметричными пассивными приемниками

Трехфазная цепь с несимметричными пассивными приемниками, включенными треугольником

Мощность в трехфазной цепи

ПЕРЕХОДНЫЕ ПРОЦЕССЫ В ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ

8.1 Основные понятия

Короткое замыкание RL цепи постоянного тока

Отключение цепи RL от источника постоянного напряжения

8.3.2 Короткое замыкание цепи RC (разряд конденсатора С на сопротивлении R )

8.3.3. Релаксационный генератор

МАГНИТНЫЕ ЦЕПИ

Расчет неразветвленной магнитной цепи

Обратная задача.

Катушка индуктивности с ферромагнитным сердечником У катушки без сердечника магнитный потокФ B Sпропорционален магнитной движущей силеF I w, а зависимость Ф(I)является линейной. При наличии магнитопровода магнитный поток катушки (дросселя) значительно возрастает при прочих равных условиях, т.к. он создается не только катушкой с током (источником внешнего магнитного поля), но и соответствующим ферромагнитным веществом магнитопровода (источником внутреннего магнитного поля).Известно, Ф B S μ H S, т.е. Ф μ, а для ферромагнитных материалов на несколько порядков выше магнитной проницаемости воздухаμ0 . Значит, одинаковый магнитный поток в катушке с магнитопроводом можно получить призначительно меньшей намагничивающей силе F I  w.Схема замещения реальной катушки индуктивности имеет вид рис.9.12. Здесь i0Рис.9.12 Рис.9.13 ток катушки; R- активное сопротивление проводов катушки; x ω L индуктивное сопротивление катушки; R0 - активное сопротивление, обусловленное потерями мощности в катушкеR PM;0 I2x0 - индуктивное сопротивление, обусловленное основным магнитным потоком. По второму закону КирхгофаU  R I jx I E . 0 0Векторная диаграмма, построенная в соответствии с данным уравнением, имеет вид (рис.10.13). Так какe  dФ, то Ф отстает по фазе от E наdtπ. Кроме того,2 0Ф отстает по фазе от тока I на угол δвследствие явления гистерезиса. Так как зависимостьB(H)– нелинейная, следовательно нелинейной будет и зависимость Ф(i0 ) (рис.9.14). Так как напряжение зависимость Ф(t) .u(t)Рис.9.14синусоидальное, значит синусоидальной будет и Но из-за нелинейностиB(H)ток катушки с сердечникомi0 (t)будет несинусоидальным (см. рис.9.14), а это значит, что нелинейная индуктивность является генератором высших гармоник тока. Из рис. 9.14 видно, что ток i0опережает по фазе поток Фна гистерезисный угол δ(ток достигает нуля раньше магнитного потока).Для катушки индуктивности с магнитопроводом, имеющим воздушный зазор (рис.9.15), по закону ОмаФ F,Rм гдеRмопределяются, в основном, сопротивлением воздушного зазора. Рис. 9.15 Рис.9.16 Увеличение воздушного зазора увеличиваетRм, а значит должно уменьшить поток Ф. Но этого не происходит, т.к. из формулыU 4,44  f w Фmследует, что ФmU4,44  f w, т.е. величина потока зависит только от действительного значения питающего напряжения, которое, естественно, не меняется. Значит, не меняется и поток. Это объясняется тем, что при увеличении δувеличивается намагничивающая силаI wдо значения, при котором поток Ф(а значит и отношениеF) остаетсяRм постоянным. Ток дросселя увеличивается за счет того, что уменьшается полное сопротивление катушки вследствие уменьшения ее реактивного сопротивления (из- за уменьшения индуктивности) (см. рис.9.16).Таким образом, путем изменения величины воздушного зазора в магнитопроводе, можно регулировать ток катушки индуктивности (дросселя) при включении ее в цепь переменного тока при неизменности питающего напряжения. В данном случае, катушка индуктивности с ферромагнитным сердечником, в цепи которого имеется регулируемый воздушный зазор, выполняет функции регулируемого сопротивления. БИБЛИОГРАФИЧЕСКИЙ СПИСОК Башарин С.А., Федоров В.В. Теоретические основы электротехники. Учебное пособие. М.: ACADEMA. 2004. – 304с. Иванов И.И., Соловьев Г.И., Равдоник В.С. Электротехника. Учебник. 3-е изд., стер. – СПб.: Издательство «Лань», 2005. – 496с., ил. Касаткин А.С., Немцов М.В. Основы электротехники для студентов вузов. – М.: Энергоатомиздат, 2000. 1   ...   48   49   50   51   52   53   54   55   56



L
C
друга ( xx,

x x x

0 ), значения тока и мощности максимальны, а от

источника в цепь поступает только активная энергия.


L
C
Частота, на которой наблюдается резонанс напряжения, определяется из

условия равенства реактивных сопротивлений на резонансной частоте

x x:

ω0 L

1 ;

ω0 C

ω2 L C 1 ;

ω 1 .


0
0
U
 При резонансе напряжения на реактивных элементах цепи равны по величине

и противоположны по фазе

U

и могут во много раз превышать напряжение


L
C
питания U (ЭДС E ). Такое превышение получается, если

ω0 L

1


ω0 C

  • R. (5.4)


0
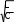 Подставив значение превышения (5.4) в виде

ω 1

в последнее выражение, получим условие

    • Rили

ρ R.


Величина

ρ

ω0

L

1


ω0 C

называется характеристическим

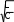сопротивлениемколебательного контура (Ом).

Отношение

ρопределяет резонансные свойства колебательного контура и

R

называется добротностьюконтура

Q ρ.

R

Если при резонансе увеличить в одинаковое число раз nиндуктивное и

емкостное сопротивления, т.е.

x n xи

x n x

, то ток I в цепи не


L
C
L0
C0
изменится, а напряжения на индуктивном и емкостном элементах увеличиваются в n

раз:

U

nUL

и U

nUC

. Следовательно, в принципе можно безгранично


L
C
увеличивать напряжения на индуктивном и емкостном элементах при одном и том же токе

I U

R

E .

R

Явление резонанса в электроэнергетических установках, как правило, явление вредное (возникающие перенапряжения, во много раз превышающие рабочие номинальные напряжения, могут привести к выходу из строя электроустановки). Но в радиотехнике, связи и автоматике оно используется часто, например, для настройки цепей на заданную частоту с целью выделения колебаний напряжения данной частоты.

В качестве примера рассмотрим входную часть радиоприемника (рис.5.32).




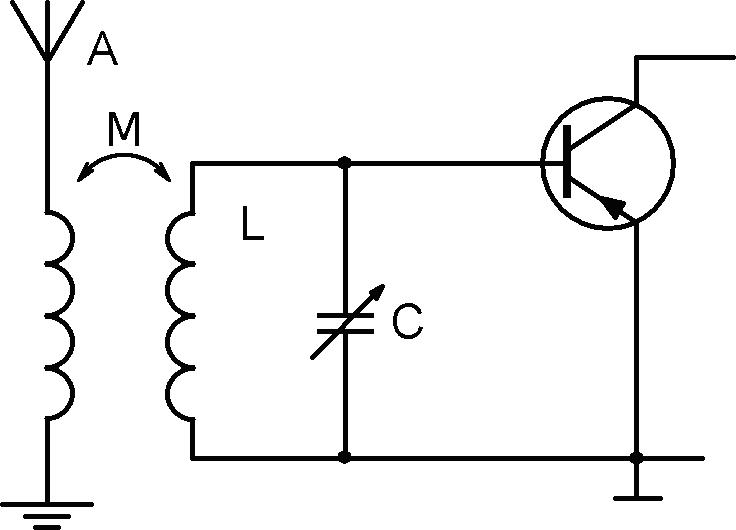
Рис.5.32

Колебательный контур LC имеет высокую добротность.

В антенне наводятся быстропеременные токи, приводящие к возникновению

в катушке L колебательного контура ЭДС взаимной индукции

E0 (сигналы от всех

работающих радиостанций). Если E0 имеет частоту, равную резонансной частоте


0
данного контура, то на конденсаторе и, соответственно, на входе транзистора

возникает напряжение равное

E Q, где Q– добротность контура. Это усиление

касается только резонансной частоты, что обеспечивает выделение из многих радиосигналов работающих радиостанций только одного (таким образом, осуществляется "настройка" на определенную радиостанцию).


и
U
Треугольник сопротивлений


Треугольник, катетами которого являются векторы

U U , а


LC
R
гипотенузой – вектор U называется треугольникомнапряжения(см. векторные диаграммы, изображенные выше).

Если стороны этого треугольника поделить на ток I , то получим треугольники сопротивлений (рис.5.33 и рис.5.34)



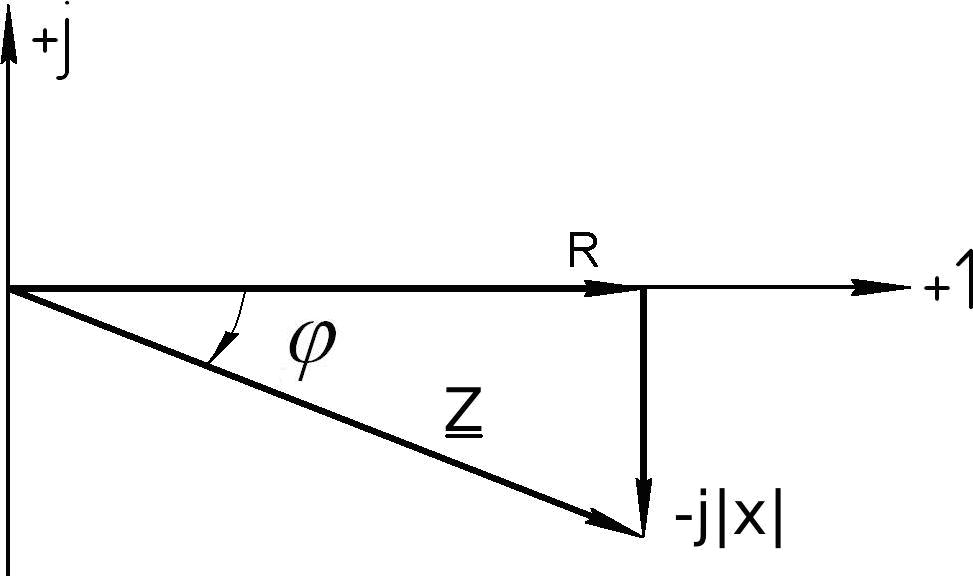
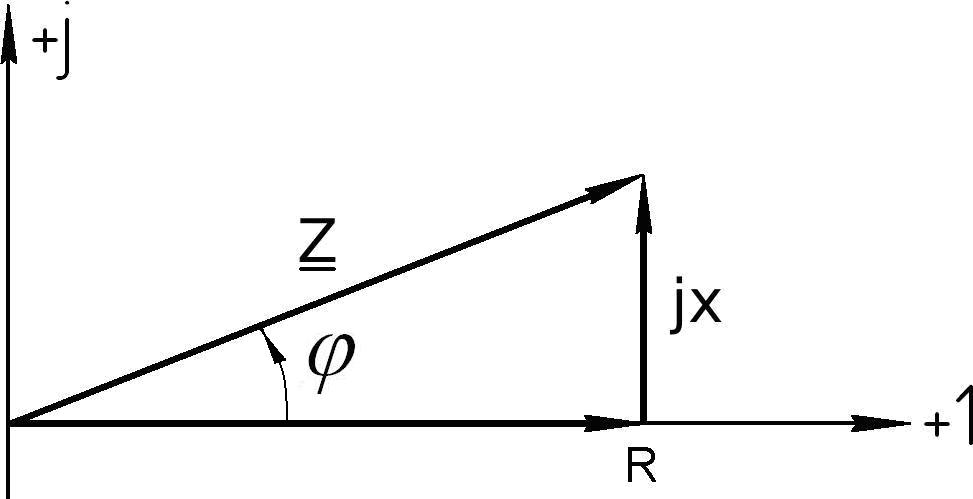
Рис.5.33 Рис.5.34

В треугольнике на рис.5.33

x 0

(преобладает емкостное сопротивление), а

треугольнике на рис.5.34

x 0

(преобладает индуктивное сопротивление).

Треугольник сопротивлений представляет собой геометрическую интерпретацию уравнения

Z R

j ω L 1 z ejφ

z cosφ

j z sinφ.

ωC


        1. Параллельное соединение R, L, C. Треугольники токов и проводимостей. Резонанс токов



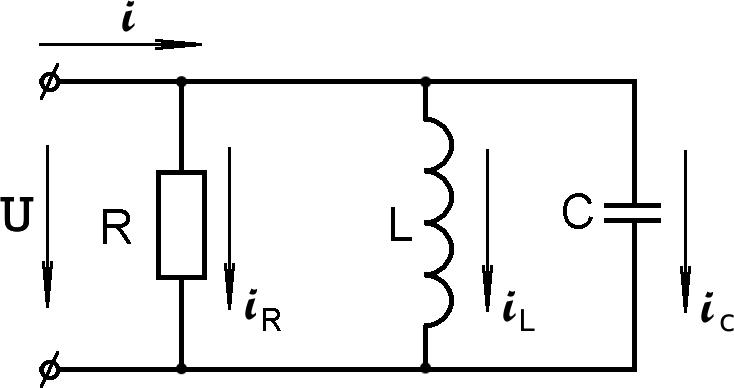Пусть на входе цепи (рис.5.35) действует

напряжение

u Umsin(ω tψu) , комплекс

которого имеет вид U U ejψu. Под

действием этого напряжения по цепи будет протекать ток i, равный

Рис.5.35

i i

i i

или

u g

1 udt CduC


L
t
0 dt

i.


L
C
R
Перепишем данное уравнение в комплексной форме:

U g U

1


jω L

U jω C I . Выполним простые преобразования:



U gj



1


ω L

jω C I ;





U g j 1 ω C I ,





ωL

U (g j b) I , U Y I ,

где g– активная проводимость; b– реактивная проводимость;
1


ω L
bL–

Смотрите также файлы