ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 11.08.2024
Просмотров: 517
Скачиваний: 0
СОДЕРЖАНИЕ
Т. Н. Матыцина е. К. Коржевина линейная алгебра
1.1. Множества и их элементы. Способы задания множеств
1.2. Подмножества. Диаграммы Эйлера – Венна
1.3. Операции над множествами и их свойства
2. Пересечение (или произведение).
4. Декартовое произведение (или прямое произведение).
Свойства операций над множествами
1.4. Метод математической индукции
Операции над комплексными числами
Геометрическая интерпретация комплексных чисел
Тригонометрическая форма комплексного числа
Действия над комплексными числами в тригонометрической форме
4. Извлечение корня n-ой степени.
Показательная форма комплексного числа
Способы задания бинарных отношений
Операции над бинарными отношениями
2.2. Свойства бинарных отношений
2.3. Отношение эквивалентности
3. Матрицы и действия над ними
3.2. Основные операции над матрицами и их свойства
3.2.1. Сложение однотипных матриц
3.2.2. Умножение матрицы на число
4. Определители квадратных матриц
4.1. Определители матриц второго и третьего порядка
4.2. Определитель матрицы n-го порядка
4.4. Практическое вычисление определителей
5. Ранг матрицы. Обратная матрица
5.2. Нахождение ранга матрицы методом окаймления миноров
5.3. Нахождение ранга матрицы с помощью элементарных преобразований
5.4. Понятие обратной матрицы и способы ее нахождения
Алгоритм нахождения обратной матрицы
Нахождение обратной матрицы с помощью элементарных преобразований
6.1. Основные понятия и определения
6.2. Методы решения систем линейных уравнений
6.3. Исследование системы линейных уравнений
6.4. Однородные системы линейных уравнений
Свойства решений однородной системы линейных уравнений
Фундаментальный набор решений однородной системы линейных уравнений
7. Арифметическое n-мерное векторное пространство
7.2. Линейная зависимость и независимость системы векторов
Свойства линейной зависимости системы векторов
Две теоремы о линейной зависимости
7.3. Базис и ранг системы векторов
8. Векторные (линейные) пространства
8.1. Определение векторного пространства над произвольным полем.
Простейшие свойства векторных пространств
Линейная зависимость и независимость системы векторов
8.2. Подпространства. Линейные многообразия
Пересечение и сумма подпространств
8.3. Базис и размерность векторного пространства
8.3.1. Конечномерные векторные пространства
Базис конечномерного векторного пространства
8.3.2. Базисы и размерности подпространств
8.3.3. Координаты вектора относительно данного базиса
8.3.4. Координаты вектора в различных базисах
8.4 Евклидовы векторные пространства
Скалярное произведение в координатах
Скалярное произведение в ортонормированном базисе
Ортогональное дополнение подпространства
9.1. Основные понятия и способы задания линейных операторов
Способы задания линейных операторов
9.2. Матрица линейного оператора Связь между координатами вектора и координатами его образа
Матрицы линейного оператора в различных базисах
Свойства отношения подобия матриц
9.4. Действия над линейными операторами
1. Сложение линейных операторов.
Свойства сложения линейных операторов
9.5. Ядро и образ линейного оператора
9.6. Обратимые линейные операторы
9.7. Собственные векторы линейного оператора
9.7.1. Свойства собственных векторов
9.7.2. Характеристический многочлен матрицы
9.7.3. Нахождение собственных векторов линейного оператора
9.7.4. Алгоритм нахождения собственных векторов линейного оператора
9.7.5.Условия, при которых матрица подобна диагональной матрице
10. Жорданова нормальная форма матрицы линейного оператора
10.2. Жорданова нормальная форма
10.3.Приведение матрицы к жордановой (нормальной) форме
Алгоритм приведения матрицы a к жордановой форме
11. Билинейные и квадратичные формы
Преобразование матрицы билинейной формы при переходе к новому базису. Ранг билинейной формы
Приведение квадратичной формы к каноническому виду
Закон инерции квадратичных форм
Классификация квадратичных форм
Необходимое и достаточное условие знакоопределенности квадратичной формы
Необходимое и достаточное условие знакопеременности квадратичной формы
Необходимое и достаточное условие квазизнакопеременности квадратичной формы
Множество считают заданным, если о любом объекте можно сказать, принадлежит он этому множеству или не принадлежит. Множество можно задать следующими способами:
перечислением всех его элементов;
характеристическим свойством элементов множества;
порождающей процедурой.
Первый способ задания множеств применим только для конечных множеств, да и то при условии, что число элементов множества невелико. Если a, b, c, d – обозначения различных объектов, то множество A этих объектов записывают так: A = {a, b, c, d}. Запись читают: «A – множество, элементы которого a, b, c, d».
Замечание 1.2. Порядок перечисления элементов множества не имеет значения. Например, множества {m, n, k, r} и {n, m, r, k} совпадают.
Вторым способом можно задавать как конечные, так и бесконечные множества. Характеристическое свойство – это такое свойство, которым обладает каждый элемент, входящий в данное множество, и не обладает ни один элемент, который ему не принадлежит. Если обозначить символом P(а) характеристическое свойство элементов множества A, то тогда используется следующая запись: A = {а P(а)}.
Порождающая процедура описывает способ получения элементов нового множества из уже полученных элементов или из других объектов. Тогда элементами множества считаются все объекты, которые могут быть получены с помощью этой процедуры. Другими словами, порождающая процедура – это процесс, который будучи запущен, порождает все элементы данного множества. С помощью порождающей процедуры можно задавать множества, содержащие любое число элементов.
Пример 1.1. Определим различными способами множество M всех нечетных натуральных чисел, не превышающих 10:
M = {1, 3, 5, 7, 9};
M = {m | m N, m < 10, m – нечетное число} или
M = {2n – 1 | n N, n 5};
порождающая процедура определяется правилами:
1 M;
если m M, то (m + 2) M, где m 7.
1.2. Подмножества. Диаграммы Эйлера – Венна
Определение 1.4. Множество B называется подмножеством множества A, если каждый элемент множества B принадлежит множеству A.
Пример 1.2. Пусть А = {1, 2, 3, 4, 5, 6, 7}, а B = {2, 3, 5, 7}. Множество В является подмножеством множества А, поскольку каждый элемент множества В принадлежит множеству А.
Если множество B является подмножеством множества A, то говорят также, что B содержится в A или B включено в A, при этом пишут В А или А В. Символ называется знаком включения (точнее, нестрого включения).
Согласно данному определению 1.4 подмножества, каждое множество является подмножеством самого себя, то есть ( A) А А. Кроме того, считается, что пустое множество есть подмножество любого множества A: ( A) А.
Различают два вида подмножеств множества А.
Определение 1.5. Пустое множество и множество А называются несобственными подмножествами множества А.
Определение 1.6. Любые подмножества множества А, отличные от А и , называются собственными подмножествами множества А.
Определение 1.7. Множества A и B, состоящие из одних и тех же элементов, называются равными. При этом пишут А = В, в противном случае А ≠ В.
Справедливо следующее утверждение, которое также можно рассматривать в качестве определения равных множеств.
Утверждение 1.1. А = В А B и В А.
Замечание 1.3. Из утверждения 1.1 вытекает способ доказательства равенства двух множеств: если доказать, что каждый элемент из множества A является элементом множества B и каждый элемент из множества B является элементом множества A, то делают вывод, что А = В.
Говорят, что множество B строго включено в множество A или, по-другому, А строго включает B, если В А и В А. В этом случае пишут B A. Символ называется знаком строгого включения.
Пример 1.3. Имеют место следующие строгие включения числовых множеств: N N0 Z Q R C и I R C.
Определение 1.8. Совокупность всех подмножеств множества A называется его булеаном (или множеством-степенью), и обозначается через P(A) (или 2A).
Пример 1.4. Если A = {a, b, c}, то булеан множества А это множество P(A) = {, {a}, {b}, {c}, {a, b}, {b, c}, {a, c}, {a, b, c}}.
Для наглядного изображения множеств и их свойств используют так называемые диаграммы Эйлера2 – Венна3. Множество отождествляется с множеством точек на плоскости, лежащих внутри некоторых замкнутых кривых, например окружностей (так называемые круги Эйлера). В частности, универсальное множество U изображается множеством точек некоторого прямоугольника или всей плоскости (рис. 1.1).

1.3. Операции над множествами и их свойства
Определим операции над множествами, с помощью которых можно получать из любых имеющихся множеств новые множества.
1. Объединение (или сумма).
Определение 1.9. Объединением множеств А и В называется множество A B, состоящее из тех и только тех элементов, которые принадлежат хотя бы одному из этих множеств.
То есть, по определению 1.9, A B = {х | х Î А или х Î В}.
Все операции над множествами можно иллюстрировать с помощью диаграмм Эйлера – Венна. Объединение множеств А и В заштриховано и изображено на рис. 1.2.
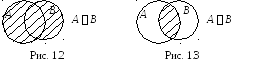
Заметим, что в объединение двух множеств A и B могут входить элементы из A, не принадлежащие множеству B, элементы из B, не принадлежащие множеству A, и элементы, принадлежащие множествам A и B одновременно. Следовательно, ( A, B) A A B и B A B.
2. Пересечение (или произведение).
Определение 1.10. Пересечением множеств А и В называется множество A B, которое состоит из тех и только тех элементов, принадлежащих одновременно и множеству А и множеству B.
Таким образом, по определению 1. 10, A B = {х | х Î А и х Î В}. Пересечение множеств А и В заштриховано и изображено на рис. 1.3.
Замечание 1.4. Если A B , то говорят, что множества A и B пересекаются. Если A B = , то в этом случае множества A и B называются непересекающимися.
Из определения пересечения следует, что ( A, B) А В А и А В В.
3. Разность.
Определение 1.11. Разностью множеств А и В называется множество А \ В, состоящее из тех и только тех элементов, которые принадлежат множеству А и одновременно не принадлежат множеству В.
Таким образом, по определению 1.11, А \ В = {x x А и х В}. Разность множеств А и В заштриховано и изображено на рис. 1.4.

Замечание 1.5. Если B A, то в этом случае разность А \ В называют дополнением B до A.
Определим частные случаи разности.
Определение 1.12. Симметрической разностью (или кольцевой суммой) множеств А и В называется множество A B (или А В), состоящее из элементов объединения этих множеств, но не входящих в пересечение этих множеств (рис. 1.5).
Таким образом, по определению, A B = (A B) \ (A B) = = (A \ B) (B \ A) = {x (x А и х В) или (x B и х A)}.
Определение 1.13. Дополнением множества А (до универсального множества U) называется множество (или A) равное разности U \ А.
Дополнение множества А до универсального множества U заштриховано и изображено на рис. 1.6.
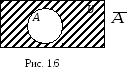
Таким образом, по определению, = U \ А = {x x U и х А} или = {x х А}.
Пример 1.5. Пусть A = {m, n, p, k, l}, B = {p, r, s, n}. Найти: A B, A B, A \ B, B \ A, A B.
Решение.
A B = {m, n, p, k, l, r, s}; A B = {p, n}; A \ B = {m, k, l}; B \ A = {r, s};
A B = { m, k, l, r, s}.
Пример 1.6.
Пусть A = {х | х Î R,
–4 х < 1},
B = {х | х Î R,
0 х 4}.
Найти:
A B,
A B,
A \ B,
B \ A,
A B,
![]() ,
,![]() .
.
Решение.
A B = {х | х Î R, –4 х 4};
A B = {х | х Î R, 0 х < 1};
A \ B = {х | х Î R, –4 х < 0};
B \ A = {х | х Î R, 1 х 4};
A B = {х | х Î R, –4 х < 0, 1 х 4};
![]() = {х | х Î R,
х < –4,
х 1};
= {х | х Î R,
х < –4,
х 1};
![]() = {х | х Î R,
х < 0,
х > 4}.
= {х | х Î R,
х < 0,
х > 4}.
4. Декартовое произведение (или прямое произведение).
Определение 1.14. Упорядоченной парой (или парой) (a, b) называется два элемента a, b взятые в определенном порядке. Пары (a1, b1) и (a2, b2) равны тогда и только тогда, когда a1 = a2 и b1 = b2.
Определение 1.15. Декартовым произведение множеств А и В называется множество А В, состоящее из всех упорядоченных пар (a, b), где a A и b B.
То есть, по определению, A B = {(x, y) | x Î А и y Î В}.
Определение 1.16. Произведение А A называется декартовым квадратом.
Пример 1.7. Пусть A = {a, b, c} и B = {5, 6}. Тогда
A B = {(a, 5), (a, 6), (b, 5), (b, 6), (c, 5), (c, 6)};