ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 11.08.2024
Просмотров: 567
Скачиваний: 0
СОДЕРЖАНИЕ
Т. Н. Матыцина е. К. Коржевина линейная алгебра
1.1. Множества и их элементы. Способы задания множеств
1.2. Подмножества. Диаграммы Эйлера – Венна
1.3. Операции над множествами и их свойства
2. Пересечение (или произведение).
4. Декартовое произведение (или прямое произведение).
Свойства операций над множествами
1.4. Метод математической индукции
Операции над комплексными числами
Геометрическая интерпретация комплексных чисел
Тригонометрическая форма комплексного числа
Действия над комплексными числами в тригонометрической форме
4. Извлечение корня n-ой степени.
Показательная форма комплексного числа
Способы задания бинарных отношений
Операции над бинарными отношениями
2.2. Свойства бинарных отношений
2.3. Отношение эквивалентности
3. Матрицы и действия над ними
3.2. Основные операции над матрицами и их свойства
3.2.1. Сложение однотипных матриц
3.2.2. Умножение матрицы на число
4. Определители квадратных матриц
4.1. Определители матриц второго и третьего порядка
4.2. Определитель матрицы n-го порядка
4.4. Практическое вычисление определителей
5. Ранг матрицы. Обратная матрица
5.2. Нахождение ранга матрицы методом окаймления миноров
5.3. Нахождение ранга матрицы с помощью элементарных преобразований
5.4. Понятие обратной матрицы и способы ее нахождения
Алгоритм нахождения обратной матрицы
Нахождение обратной матрицы с помощью элементарных преобразований
6.1. Основные понятия и определения
6.2. Методы решения систем линейных уравнений
6.3. Исследование системы линейных уравнений
6.4. Однородные системы линейных уравнений
Свойства решений однородной системы линейных уравнений
Фундаментальный набор решений однородной системы линейных уравнений
7. Арифметическое n-мерное векторное пространство
7.2. Линейная зависимость и независимость системы векторов
Свойства линейной зависимости системы векторов
Две теоремы о линейной зависимости
7.3. Базис и ранг системы векторов
8. Векторные (линейные) пространства
8.1. Определение векторного пространства над произвольным полем.
Простейшие свойства векторных пространств
Линейная зависимость и независимость системы векторов
8.2. Подпространства. Линейные многообразия
Пересечение и сумма подпространств
8.3. Базис и размерность векторного пространства
8.3.1. Конечномерные векторные пространства
Базис конечномерного векторного пространства
8.3.2. Базисы и размерности подпространств
8.3.3. Координаты вектора относительно данного базиса
8.3.4. Координаты вектора в различных базисах
8.4 Евклидовы векторные пространства
Скалярное произведение в координатах
Скалярное произведение в ортонормированном базисе
Ортогональное дополнение подпространства
9.1. Основные понятия и способы задания линейных операторов
Способы задания линейных операторов
9.2. Матрица линейного оператора Связь между координатами вектора и координатами его образа
Матрицы линейного оператора в различных базисах
Свойства отношения подобия матриц
9.4. Действия над линейными операторами
1. Сложение линейных операторов.
Свойства сложения линейных операторов
9.5. Ядро и образ линейного оператора
9.6. Обратимые линейные операторы
9.7. Собственные векторы линейного оператора
9.7.1. Свойства собственных векторов
9.7.2. Характеристический многочлен матрицы
9.7.3. Нахождение собственных векторов линейного оператора
9.7.4. Алгоритм нахождения собственных векторов линейного оператора
9.7.5.Условия, при которых матрица подобна диагональной матрице
10. Жорданова нормальная форма матрицы линейного оператора
10.2. Жорданова нормальная форма
10.3.Приведение матрицы к жордановой (нормальной) форме
Алгоритм приведения матрицы a к жордановой форме
11. Билинейные и квадратичные формы
Преобразование матрицы билинейной формы при переходе к новому базису. Ранг билинейной формы
Приведение квадратичной формы к каноническому виду
Закон инерции квадратичных форм
Классификация квадратичных форм
Необходимое и достаточное условие знакоопределенности квадратичной формы
Необходимое и достаточное условие знакопеременности квадратичной формы
Необходимое и достаточное условие квазизнакопеременности квадратичной формы
Определение 1.17.
Комплексным
числом
называется выражение вида a + bi,
где a,
b R,
i = ![]() – мнимая единица.
– мнимая единица.
Комплексное число z = a + bi состоит из двух частей: число а = Rez– называется действительной частью z, b = Imz – мнимой частью комплексного числа z.
Используют
следующие термины: если b = 0,
то a + 0i = а
– действительное число (точнее
отождествляют с действительным числом),
в частности 0 + 0i = 0;
если а = 0,
то числа вида bi
(b ≠ 0)
называют чисто
мнимым.
Множество всех комплексных чисел
обозначают C = {a + bi
| a,
b R,
i = ![]() }
при этом R C.
}
при этом R C.
Определение 1.18. Комплексное число, записанное в виде z = a + bi, называется алгебраической формой записи комплексного числа.
Определение 1.18. Два комплексных числа равны тогда и только тогда, когда равны их действительные и мнимые части равны, т. е. a + bi = с + di a + с и b = d.
Определение 1.19. Комплексные числа вида a + bi и a – bi называются сопряженными.
Определение 1.20. Комплексные числа вида a + bi и –a – bi называются противоположными.
Операции над комплексными числами
Сложение: (a + bi) + (с + di) = (а + с) + (b + d)i, при сложении двух комплексных чисел их действительные части и мнимые части складываются.
Вычитание: (a + bi) – (с + di) = (а – с) + (b – d)i.
Умножение: (a + bi)(с + di) = (ас – bd) + (ad + bc)i, это простое умножение двучлена a + bi на с + di с последующей заменой i2 на –1.
Деление:
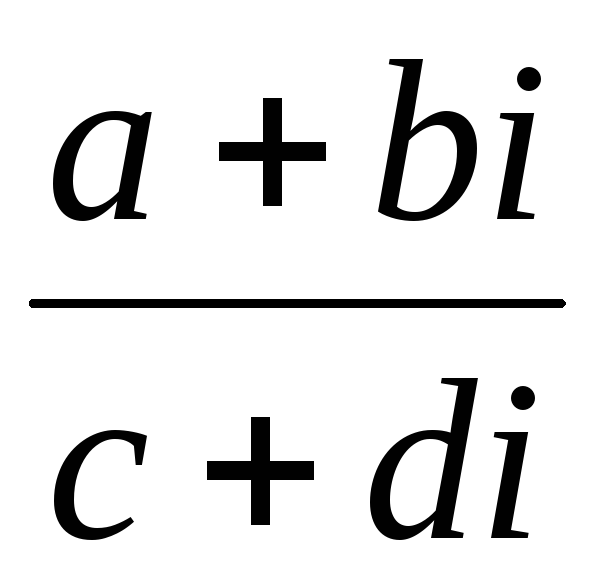 =
= 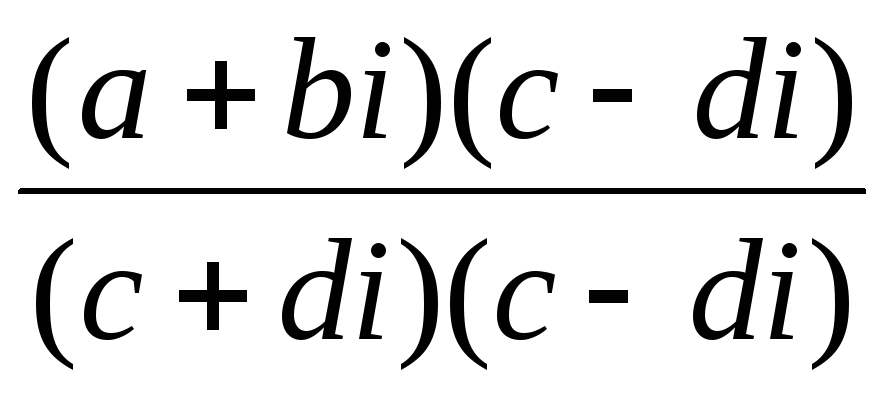 =
= 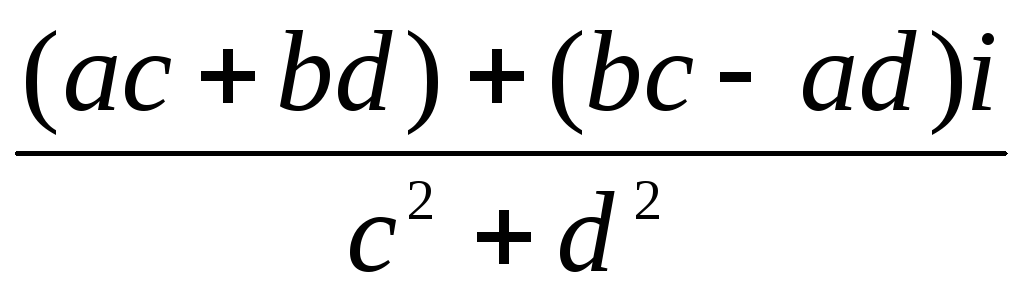 =
=
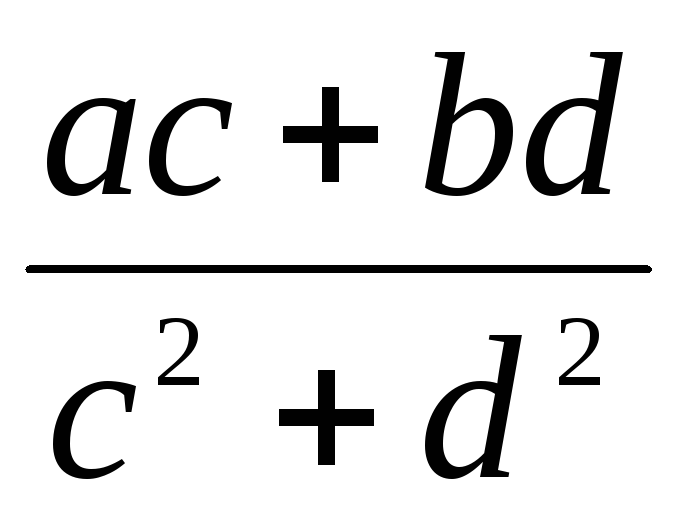 +
+
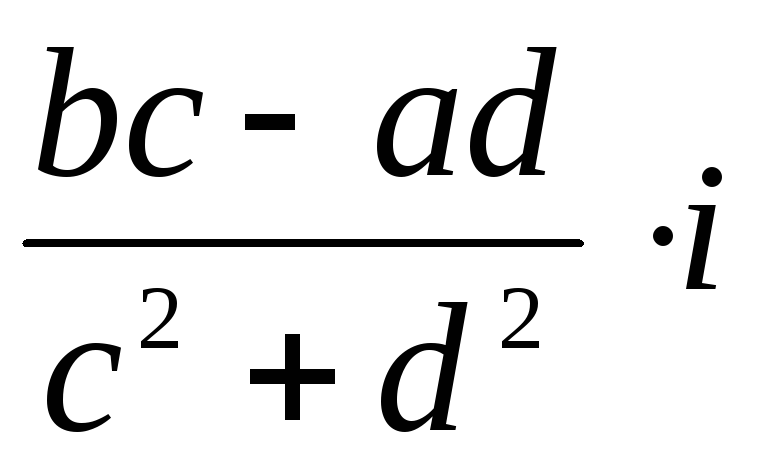 ,
если с + di ≠ 0.
,
если с + di ≠ 0.
Геометрическая интерпретация комплексных чисел
Известно, что отрицательные числа были введены в связи с решением линейных уравнений с одной переменной. В конкретных задачах отрицательный ответ истолковывался как значение направленной величины (положительные или отрицательные температуры, передвижение в противоположных направлениях, прибыль и долг и т. д.). Однако еще в 16 веке многие математики не признавали отрицательных чисел. Только с введением координатной прямой и координатной плоскости отчетливо проявился смысл отрицательных чисел, и они стали такими же «равноправными» и понятными, как и натуральные числа. Аналогично обстоит дело и комплексными числами. Смысл их отчетливо проявляется при введении их геометрической интерпретации.

Геометрическое представление комплексных чисел состоит в том, что каждому комплексному числу z = a + bi ставится в соответствие точка М(а, b) плоскости в прямоугольной системе координат (рис. 1.9, а), таким образом, что действительная часть комплексного числа представляет собой абсциссу, а мнимая – ординату точки. Или вместо точки можно поставить в соответствие вектор с координатами (а, b) (рис. 1.9, б). Таким образом, устанавливается взаимно однозначное соответствие между множеством комплексных чисел и множеством точек координатной плоскости.
Ясно, что действительное число a + 0i = а изображается точкой на оси Ох, а чисто мнимое число 0 + bi, где b ≠ 0 – точкой на оси Oy. Поэтому ось Oy называется мнимой, а ось Ох – действительной.
С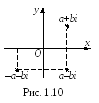 опряженные
комплексные числаa + bi
и
a – bi
изображаются точками симметричными
относительно оси Ох,
а противоположные комплексные числа
a + bi
и –a – bi
– точками симметричными относительно
начала координат (рис. 1.10).
опряженные
комплексные числаa + bi
и
a – bi
изображаются точками симметричными
относительно оси Ох,
а противоположные комплексные числа
a + bi
и –a – bi
– точками симметричными относительно
начала координат (рис. 1.10).
Тригонометрическая форма комплексного числа
Вектор
![]() можно задать не только координатами в
прямоугольной системе координат, но и
длиной и углом, который он образует с
некоторым фиксированным направлением
(полярная система координат), т. е.
задать вектор
можно задать не только координатами в
прямоугольной системе координат, но и
длиной и углом, который он образует с
некоторым фиксированным направлением
(полярная система координат), т. е.
задать вектор
![]() полярными координатами (рис. 1.11).
полярными координатами (рис. 1.11).
О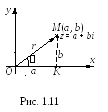 пределение 1.21.
Длина вектора, соответствующего
комплексному числу z
(или расстояние от начала системы
координат до точки, изображающей
комплексное число) называется модулем
комплексного числа и обозначается
|z| = r.
пределение 1.21.
Длина вектора, соответствующего
комплексному числу z
(или расстояние от начала системы
координат до точки, изображающей
комплексное число) называется модулем
комплексного числа и обозначается
|z| = r.
Определение 1.22. Радианная мера угла, образованного этим вектором с положительным направлением действительной оси Ох называется аргументом комплексного числа z и обозначается Аrg z = .
Другими словами, аргумент комплексного числа – это угол между положительной полуосью Ох и лучом Oz.
Число ноль изображается нуль-вектором, для него модуль равен 0, аргумент нуля не определен. Для ненулевого комплексного числа z аргумент определяется с точностью до 2k, где k – любое целое число.
Главным
значение аргумента
называется такое значение ,
что
(–,
].
Часто главное значение аргумента
обозначается аrg z.
Главное значение аргумента обратного
комплексного числа отличается знаком
аргумента исходного, т. е. аrg![]() = –аrg(z).
= –аrg(z).
Для комплексного числа z = a + bi установим связь между числами a, b и r, , т. е. между декартовыми и полярными координатами.
Рассмотрим
прямоугольный треугольник OMK
(рис. 1.11), по теореме Пифагора имеем:
OM2 = OK2 + MK2
r2 = a2 + b2
r = ![]() ,
a = rcos,
b = rsin.
Тогда
z = a + bi = rcos + rsini = r(cos + isin).
,
a = rcos,
b = rsin.
Тогда
z = a + bi = rcos + rsini = r(cos + isin).
Определение 1.23. Выражение z = r(cos + isin) называется тригонометрической формой комплексного числа.
Формулы перехода от алгебраической формы комплексного числа z = a + bi к тригонометрической следующие:
r = ![]() ,
sin =
,
sin = ![]() =
=![]() ,cos =
,cos = ![]() =
=![]() .
.
Если
a ≠ 0,
то
tg = ![]() .Можно
найти аргумент числа z,
пользуясь правилом:
.Можно
найти аргумент числа z,
пользуясь правилом:
a > 0
= ![]() ,
,
a < 0
= ![]() +,
+,
a = 0
1)
b > 0
= ![]() ,
2)b < 0
= –
,
2)b < 0
= –![]() .
.
Определение 1.24. r1(cos1 + isin1) = r2(cos2 + isin2) r1 = r2 и 1 = 2 + 2k, k Z.
Пример 1.12.
Представить следующие комплексные
числа в тригонометрической форме:
z1 = ![]() – i,
z2 = –3i,
z3 = –8,
z4 = –2(cos
– i,
z2 = –3i,
z3 = –8,
z4 = –2(cos![]() – isin
– isin![]() ),
),
Решение.
а) z1 = ![]() – i
a =
– i
a = ![]() ,
b = –1.
Найдем модуль и аргумент данного числа:
r =
,
b = –1.
Найдем модуль и аргумент данного числа:
r = ![]() =
= ![]() = 2;
т. к.
a =
= 2;
т. к.
a = ![]() > 0,
то =
> 0,
то = ![]() =
= ![]() = –
= –![]() .
.
Окончательно
получаем тригонометрическую форму
z1 = ![]() – i =
= r(cos + isin) = 2(cos
– i =
= r(cos + isin) = 2(cos![]() + isin
+ isin![]() ).
).
б) z2 = –3i
a = 0,
b = –3.
Найдем модуль и аргумент данного числа:
r = ![]() =
= ![]() = 3;
т. к.
a = 0
и b < 0,
то = –
= 3;
т. к.
a = 0
и b < 0,
то = –![]() .
.