ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 11.08.2024
Просмотров: 557
Скачиваний: 0
СОДЕРЖАНИЕ
Т. Н. Матыцина е. К. Коржевина линейная алгебра
1.1. Множества и их элементы. Способы задания множеств
1.2. Подмножества. Диаграммы Эйлера – Венна
1.3. Операции над множествами и их свойства
2. Пересечение (или произведение).
4. Декартовое произведение (или прямое произведение).
Свойства операций над множествами
1.4. Метод математической индукции
Операции над комплексными числами
Геометрическая интерпретация комплексных чисел
Тригонометрическая форма комплексного числа
Действия над комплексными числами в тригонометрической форме
4. Извлечение корня n-ой степени.
Показательная форма комплексного числа
Способы задания бинарных отношений
Операции над бинарными отношениями
2.2. Свойства бинарных отношений
2.3. Отношение эквивалентности
3. Матрицы и действия над ними
3.2. Основные операции над матрицами и их свойства
3.2.1. Сложение однотипных матриц
3.2.2. Умножение матрицы на число
4. Определители квадратных матриц
4.1. Определители матриц второго и третьего порядка
4.2. Определитель матрицы n-го порядка
4.4. Практическое вычисление определителей
5. Ранг матрицы. Обратная матрица
5.2. Нахождение ранга матрицы методом окаймления миноров
5.3. Нахождение ранга матрицы с помощью элементарных преобразований
5.4. Понятие обратной матрицы и способы ее нахождения
Алгоритм нахождения обратной матрицы
Нахождение обратной матрицы с помощью элементарных преобразований
6.1. Основные понятия и определения
6.2. Методы решения систем линейных уравнений
6.3. Исследование системы линейных уравнений
6.4. Однородные системы линейных уравнений
Свойства решений однородной системы линейных уравнений
Фундаментальный набор решений однородной системы линейных уравнений
7. Арифметическое n-мерное векторное пространство
7.2. Линейная зависимость и независимость системы векторов
Свойства линейной зависимости системы векторов
Две теоремы о линейной зависимости
7.3. Базис и ранг системы векторов
8. Векторные (линейные) пространства
8.1. Определение векторного пространства над произвольным полем.
Простейшие свойства векторных пространств
Линейная зависимость и независимость системы векторов
8.2. Подпространства. Линейные многообразия
Пересечение и сумма подпространств
8.3. Базис и размерность векторного пространства
8.3.1. Конечномерные векторные пространства
Базис конечномерного векторного пространства
8.3.2. Базисы и размерности подпространств
8.3.3. Координаты вектора относительно данного базиса
8.3.4. Координаты вектора в различных базисах
8.4 Евклидовы векторные пространства
Скалярное произведение в координатах
Скалярное произведение в ортонормированном базисе
Ортогональное дополнение подпространства
9.1. Основные понятия и способы задания линейных операторов
Способы задания линейных операторов
9.2. Матрица линейного оператора Связь между координатами вектора и координатами его образа
Матрицы линейного оператора в различных базисах
Свойства отношения подобия матриц
9.4. Действия над линейными операторами
1. Сложение линейных операторов.
Свойства сложения линейных операторов
9.5. Ядро и образ линейного оператора
9.6. Обратимые линейные операторы
9.7. Собственные векторы линейного оператора
9.7.1. Свойства собственных векторов
9.7.2. Характеристический многочлен матрицы
9.7.3. Нахождение собственных векторов линейного оператора
9.7.4. Алгоритм нахождения собственных векторов линейного оператора
9.7.5.Условия, при которых матрица подобна диагональной матрице
10. Жорданова нормальная форма матрицы линейного оператора
10.2. Жорданова нормальная форма
10.3.Приведение матрицы к жордановой (нормальной) форме
Алгоритм приведения матрицы a к жордановой форме
11. Билинейные и квадратичные формы
Преобразование матрицы билинейной формы при переходе к новому базису. Ранг билинейной формы
Приведение квадратичной формы к каноническому виду
Закон инерции квадратичных форм
Классификация квадратичных форм
Необходимое и достаточное условие знакоопределенности квадратичной формы
Необходимое и достаточное условие знакопеременности квадратичной формы
Необходимое и достаточное условие квазизнакопеременности квадратичной формы
Пример 11.1. Привести к каноническому виду квадратичную форму A(x, x) = 2x1x2 – 6x2x3 + 2x3x1.
Решение. Поскольку a11 = 0, используем преобразование
x1 = y1 – y2,
x2 = y1 + y2,
x3 = y3.
Это
преобразование имеет матрицу A =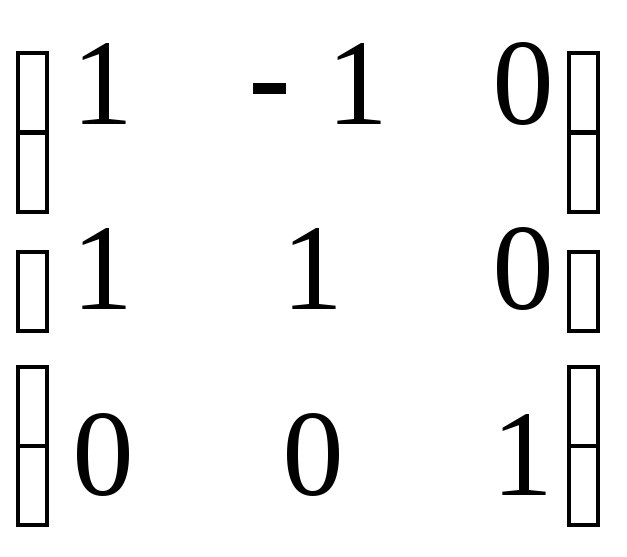 
,
то есть [x] = A[y]
получим A(x,
x) = 2(y1 – y2)(y1 + y2) – 6(y1 + y2)y3 + 2y3(y1 – y2) =
= 2
– 2
– 6y1y3 – 6y2y3 + 2y3y1 – 2y3y2= 2
– 2
– 4y1y3 – 8y3y2.
Поскольку
коэффициент при
не равен нулю, можно выделить квадрат
одного неизвестного, пусть это будет
y1.
Выделим все члены, содержащие y1.
A(x,
x) = 2(
– 2
y1y3) – 2
– 8y3y2 = 2(
– 2
y1y3 + 
) – 2
– 2
– 8y3y2 = 2(y1 – y3)2 – 2
– 2
– 8y3y2.
Выполним преобразование, матрица которого равна B.
z1 = y1 – y3, y1 = z1 + z3,
z2 = y2, y2 = z2,
z3 = y3; y3 = z3.
B =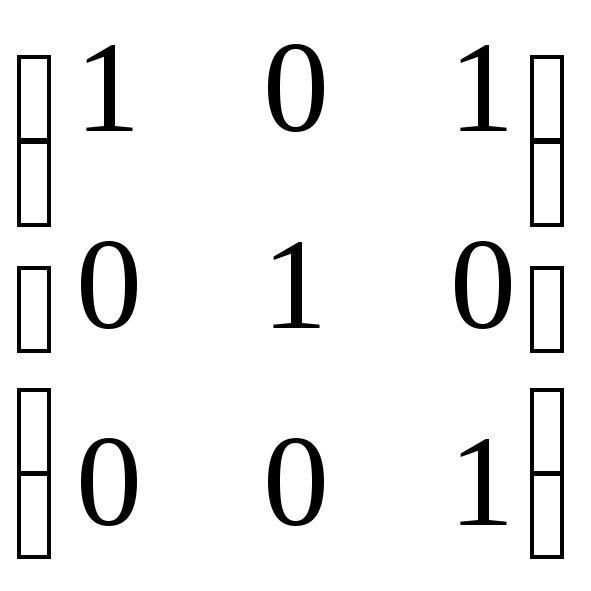 
,
[y] = B[z].
Получим
A(x,
x) = 2
– 2
–
– 8z2z3.
Выделим
члены, содержащие z2.
Имеем
A(x, x) = 2
– 2(
+ 4z2z3) – 2
= 2
– 2(
+ 4z2z3 + 4
) +
+ 8
– 2
= 2
– 2(z2 + 2z3)2 + 6
.
Выполняем преобразование с матрицей C:
t1 = z1, z1 = t1,
t2 = z2 + 2z3, z2 = t2 – 2t3,
t3 = z3; z3 = t3.
C =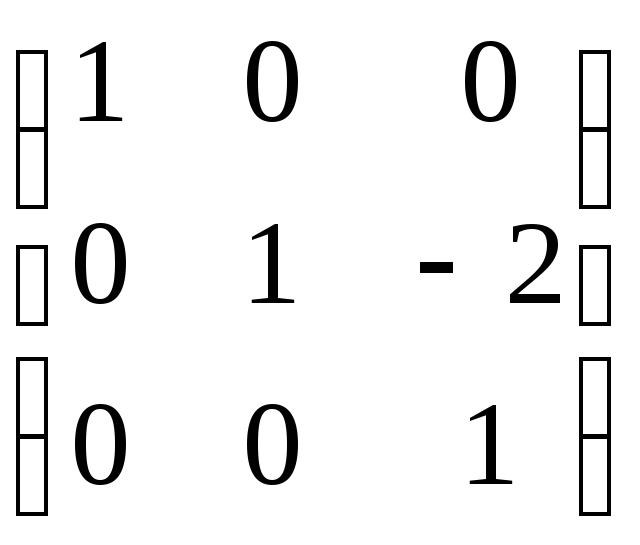 
,
[z] = C[t].
Получили:
A(x,
x) = 2
– 2
+ 6
канонический вид квадратичной формы,
при этом [x] = A[y],
[y] = B[z],
[z] = C[t],
отсюда [x] = ABC[t];
ABC =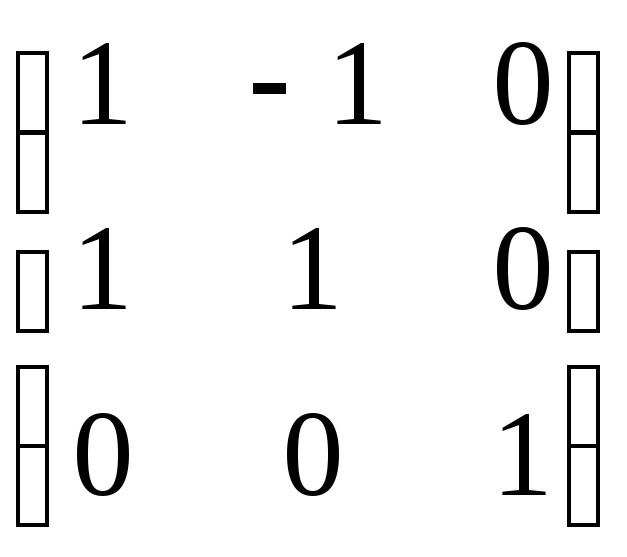 
= 
.
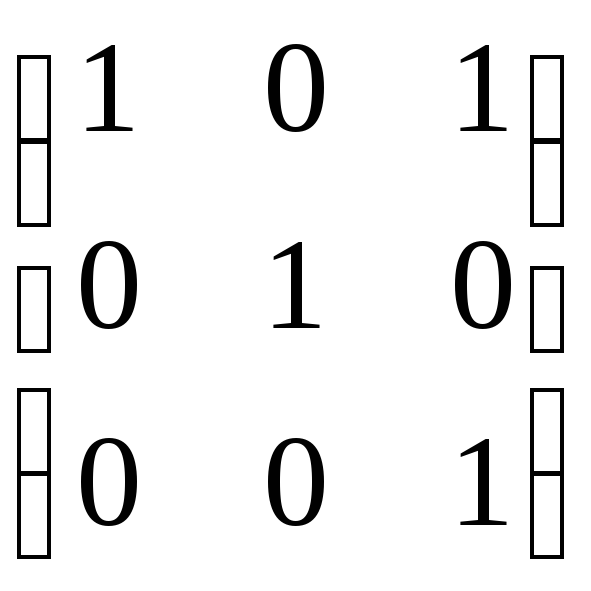
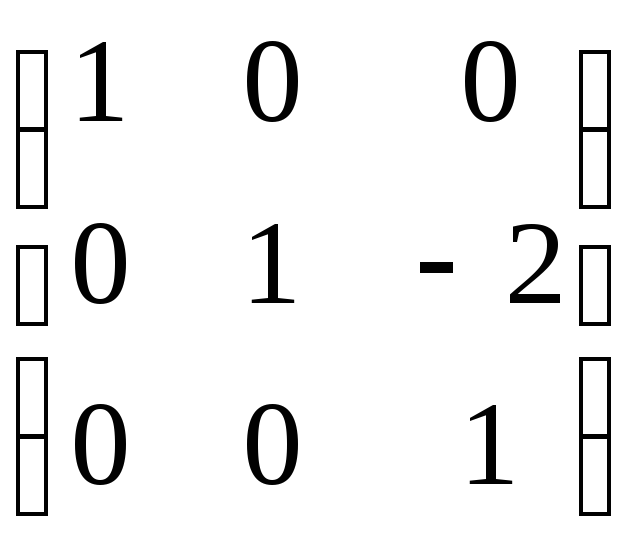Формулы преобразований следующие
x1 = t1 – t2 + t3,
x2 = t1 + t2 – t3,
x3 = t3.
Закон инерции квадратичных форм
Установлено, что число отличных от нуля канонических коэффициентов квадратичной формы равно ее рангу и не зависит от выбора невырожденного преобразования, с помощью которого форма A(x, x) приводится к каноническому виду. На самом деле не меняется и число положительных и отрицательных коэффициентов.
Теорема 11.3 (закон инерции квадратичных форм). Число положительных и отрицательных коэффициентов в нормальном виде квадратичной формы не зависит от способа приведения квадратичной формы к нормальному виду.
Пусть квадратичная форма f ранга r от n неизвестных x1, x2, …, xn двумя способами приведена к нормальному виду, то есть
f = 
+ 
+ … + 
– 
– … – 
,
f = 
+ 
+ … + 
– 
– … – 
.
Можно доказать, что k = l.
Определение 11.14. Число положительных квадратов в нормальной форме, к которой приводится действительная квадратичная форма, называется положительным индексом инерции этой формы; число отрицательных квадратов – отрицательным индексом инерции, а их сумма – индексом инерции квадратичной формы или сигнатурой формы f.
Если p – положительный индекс инерции; q – отрицательный индекс инерции; k = r = p + q – индекс инерции.
Классификация квадратичных форм
Пусть у квадратичной формы A(x, x) индекс инерции равен k, положительный индекс инерции равен p , отрицательный индекс инерции равен q, тогда k = p + q.
Было
доказано, что в любом каноническом
базисе f = {f1,
f2,
…, fn}
эта квадратичная форма A(x,
x)
может быть приведена к нормальному виду
A(x,
x) = 
+ 
+ … + 
– 
– … – 
,
где 1,
2,
…, n
координаты
вектора x
в базисе {f}.
Необходимое и достаточное условие знакоопределенности квадратичной формы
Утверждение 11.1. Для того чтобы квадратичная форма A(x, x), заданная в n-мерном векторном пространстве V, была знакоопределенной, необходимо и достаточно, чтобы либо положительный индекс инерции p, либо отрицательный индекс инерции q, был равен размерности n пространства V.
При этом если p = n, то форма положительно определена (то есть для любого x ≠ 0 A(x, x) > 0).
Если же q = n, то форма отрицательно определена (то есть для любого x ≠ 0 A(x, x) < 0).
Необходимое и достаточное условие знакопеременности квадратичной формы
Утверждение 11.2. Для того чтобы квадратичная форма A(x, x), заданная в n-мерном векторном пространстве V, была знакопеременной (то есть существуют такие x, y что A(x, x) > 0 и A(y, y) < 0) необходимо и достаточно, чтобы как положительный, так и отрицательный индексы инерции этой формы были отличны от нуля.
Необходимое и достаточное условие квазизнакопеременности квадратичной формы
Утверждение 11.3. Для того чтобы квадратичная форма A(x, x), заданная в n-мерном векторном пространстве V, была квазизнакопеременной (то есть для любого вектора x или A(x, x) ≥ 0 или A(x, x) ≤ 0 и найдется такой ненулевой вектор x, что A(x, x) = 0) необходимо и достаточно, чтобы выполнялось одно из двух соотношений: p < n, q = 0 или p = 0, q < n.
Замечание. Для того чтобы применять эти признаки, квадратичную форму надо привести к каноническому виду. В критерии знакоопределенности Сильвестра15 этого не требуется.