ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 11.08.2024
Просмотров: 601
Скачиваний: 0
СОДЕРЖАНИЕ
Т. Н. Матыцина е. К. Коржевина линейная алгебра
1.1. Множества и их элементы. Способы задания множеств
1.2. Подмножества. Диаграммы Эйлера – Венна
1.3. Операции над множествами и их свойства
2. Пересечение (или произведение).
4. Декартовое произведение (или прямое произведение).
Свойства операций над множествами
1.4. Метод математической индукции
Операции над комплексными числами
Геометрическая интерпретация комплексных чисел
Тригонометрическая форма комплексного числа
Действия над комплексными числами в тригонометрической форме
4. Извлечение корня n-ой степени.
Показательная форма комплексного числа
Способы задания бинарных отношений
Операции над бинарными отношениями
2.2. Свойства бинарных отношений
2.3. Отношение эквивалентности
3. Матрицы и действия над ними
3.2. Основные операции над матрицами и их свойства
3.2.1. Сложение однотипных матриц
3.2.2. Умножение матрицы на число
4. Определители квадратных матриц
4.1. Определители матриц второго и третьего порядка
4.2. Определитель матрицы n-го порядка
4.4. Практическое вычисление определителей
5. Ранг матрицы. Обратная матрица
5.2. Нахождение ранга матрицы методом окаймления миноров
5.3. Нахождение ранга матрицы с помощью элементарных преобразований
5.4. Понятие обратной матрицы и способы ее нахождения
Алгоритм нахождения обратной матрицы
Нахождение обратной матрицы с помощью элементарных преобразований
6.1. Основные понятия и определения
6.2. Методы решения систем линейных уравнений
6.3. Исследование системы линейных уравнений
6.4. Однородные системы линейных уравнений
Свойства решений однородной системы линейных уравнений
Фундаментальный набор решений однородной системы линейных уравнений
7. Арифметическое n-мерное векторное пространство
7.2. Линейная зависимость и независимость системы векторов
Свойства линейной зависимости системы векторов
Две теоремы о линейной зависимости
7.3. Базис и ранг системы векторов
8. Векторные (линейные) пространства
8.1. Определение векторного пространства над произвольным полем.
Простейшие свойства векторных пространств
Линейная зависимость и независимость системы векторов
8.2. Подпространства. Линейные многообразия
Пересечение и сумма подпространств
8.3. Базис и размерность векторного пространства
8.3.1. Конечномерные векторные пространства
Базис конечномерного векторного пространства
8.3.2. Базисы и размерности подпространств
8.3.3. Координаты вектора относительно данного базиса
8.3.4. Координаты вектора в различных базисах
8.4 Евклидовы векторные пространства
Скалярное произведение в координатах
Скалярное произведение в ортонормированном базисе
Ортогональное дополнение подпространства
9.1. Основные понятия и способы задания линейных операторов
Способы задания линейных операторов
9.2. Матрица линейного оператора Связь между координатами вектора и координатами его образа
Матрицы линейного оператора в различных базисах
Свойства отношения подобия матриц
9.4. Действия над линейными операторами
1. Сложение линейных операторов.
Свойства сложения линейных операторов
9.5. Ядро и образ линейного оператора
9.6. Обратимые линейные операторы
9.7. Собственные векторы линейного оператора
9.7.1. Свойства собственных векторов
9.7.2. Характеристический многочлен матрицы
9.7.3. Нахождение собственных векторов линейного оператора
9.7.4. Алгоритм нахождения собственных векторов линейного оператора
9.7.5.Условия, при которых матрица подобна диагональной матрице
10. Жорданова нормальная форма матрицы линейного оператора
10.2. Жорданова нормальная форма
10.3.Приведение матрицы к жордановой (нормальной) форме
Алгоритм приведения матрицы a к жордановой форме
11. Билинейные и квадратичные формы
Преобразование матрицы билинейной формы при переходе к новому базису. Ранг билинейной формы
Приведение квадратичной формы к каноническому виду
Закон инерции квадратичных форм
Классификация квадратичных форм
Необходимое и достаточное условие знакоопределенности квадратичной формы
Необходимое и достаточное условие знакопеременности квадратичной формы
Необходимое и достаточное условие квазизнакопеременности квадратичной формы
8.4 Евклидовы векторные пространства
Дано векторное пространство V над полем действительных чисел. Это пространство может быть как конечномерным векторным пространством размерности n, так и бесконечномерным.
Определение 8.15. Векторное пространство V называется евклидовым векторным пространством, если задано правило, по которому любой паре векторов ставится в соответствие единственное действительное число, обозначаемое (x, y) и называемое скалярным произведением векторов x и y (другими словами, задано отображение V V R). При этом указанное правило подчинено 4 аксиомам:
(x, y) = (y, x);
(x + y, z) = (x, z) + (y, z);
(x, y) = (x, y), где R;
(x, x) 0, причем (x, x) = 0 x = о; при этом (x, x) называют скалярным квадратом элемента х.
Пример 8.10. Приведем примеры евклидовых пространств.
1. V = Rn
– арифметическое n-мерное
векторное пространство. Если векторам
x = (x1,
x2,
…, xn)
и y = (y1,
y2,
…, yn)
поставлено в соответствие число
(x, y) = x1y1 + x2y2 + … + xnyn,
то аксиомы выполняются. Проверим
последнюю из них. Найдем (x,
x):
(x,
x) = 
.
Сумма
квадратов во множестве действительных
чисел неотрицательна. Полученное
евклидово векторное пространство
называется стандартным
евклидовым векторным пространством.
2. V – пространство направленных отрезков с общим началом в начале координат. Скалярным произведением двух векторов назовем число, равное произведению длин этих векторов на косинус угла между ними. Все требуемые свойства выполняются, что известно еще из школы.
3. V = R(a,
b)
– множество функций, заданных и
непрерывных на промежутке [a,
b].
Зададим скалярное умножение векторов
из R(a,
b)
следующим способом:
.
Из
свойств определенного интеграла
получаются все свойства, требуемые в
определении скалярного произведения.
Скалярное произведение в координатах
В евклидовом векторном пространстве V размерности n задан базис e1, e2, …, en. Векторы x и y разложены по векторам базиса: x = x1e1 + x2e2 + … + xnen, y = y1e1 + y2e2 + … + ynen. Найдем скалярное произведение этих векторов
(x, y) = (x1e1 + x2e2 + … + xnen)(y1e1 + y2e2 + … + ynen) =
= x1 y1(e1, e1) + x1 y2(e1, e2) + … + x1 yn(e1, en) + … + xn yn(en, en) =
= 
.
Очевидно,
что для задания скалярного произведения,
необходимо задать матрицу A =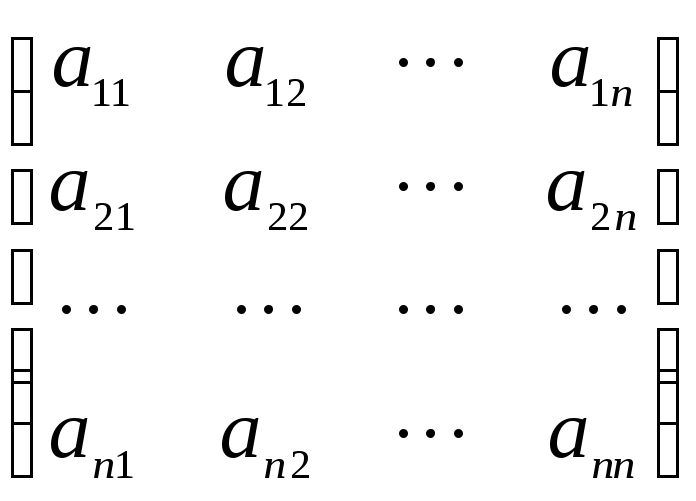 
,
где aij = (ei,
ej).
Если (x1,
x2,
…, xn)
– строка координат вектора x,
а
– столбец координат вектора y,
то (x, y) = (x1,
x2,
…, xn)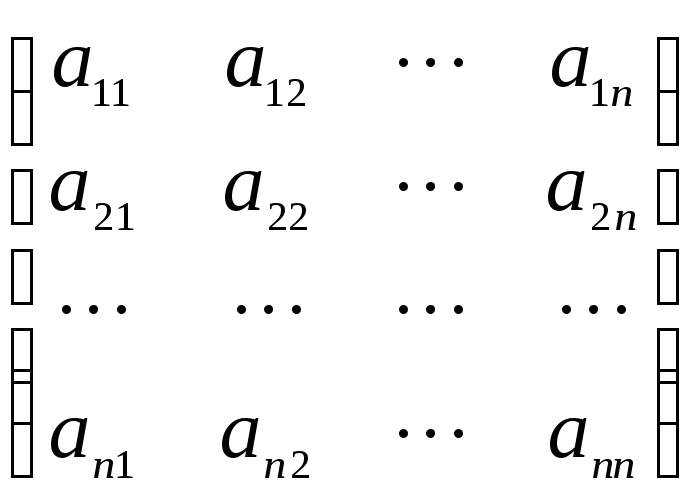
.
Матрица A не может быть произвольной, иначе не станут выполняться аксиомы евклидова векторного пространства. Эта матрица должна быть симметрической и должна задавать положительно определенную квадратичную форму. Простейшим примером такой матрицы является матрица E. При этом (x, y) = x1y1 + x2y2 + … + xnyn, то есть скалярное произведение равно сумме произведений соответствующих координат.
Метрические понятия
В евклидовых векторных пространствах от введенного скалярного произведения можно перейти к понятиям нормы вектора и угла между векторами.
Определение 8.16.
Нормой
(длиной,
модулем)
вектора а
называется число, равное корню из
скалярного квадрата вектора а:
||a|| = 
.
Поскольку (а, а) 0, то норма вектора определена.
Определение 8.17. Вектор а называется нормированным, если его норма равна единице, т. е. ||a|| = 1.
Свойства нормы
||a|| = 0 a = о.
||a|| = ||||a||, т. к. ||a|| =
= 
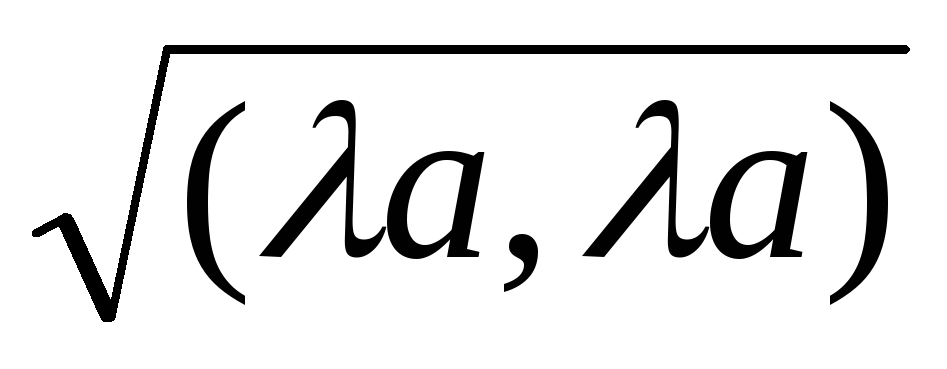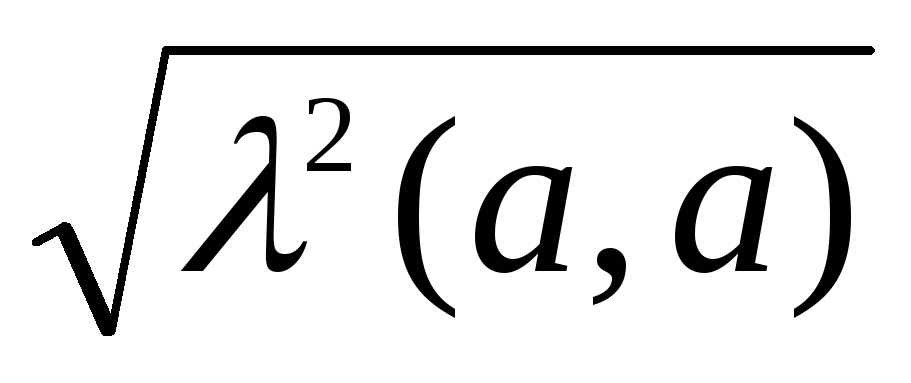= ||||a||.Неравенство Коши – Буняковского: |(а, b)| ||a||||b||.
Доказательство. Для любого числа λ и любых векторов a, b ≠ 0 выполняется условие (a – b, a – b) 0 (a, a) – 2(a, b) + 2(b, b) 0. Квадратный трехчлен относительно λ неотрицателен при любом λ, если его дискриминант неположителен: D = 4(a, b)2 – 4(a, a)(b, b) 0 (a, b)2 ||a||2||b||2 |(a, b)| ||a||||b||.
Неравенство треугольника: ||a + b|| ||a|| + ||b||.
Пример 8.11. Будем считать (если нет специальных оговорок), что скалярное произведение равно сумме произведений соответствующих координат.
Найти норму вектора а = (
,
,
).
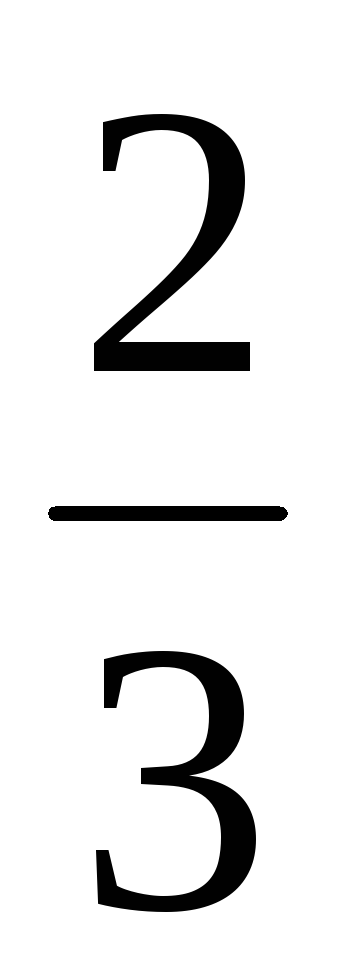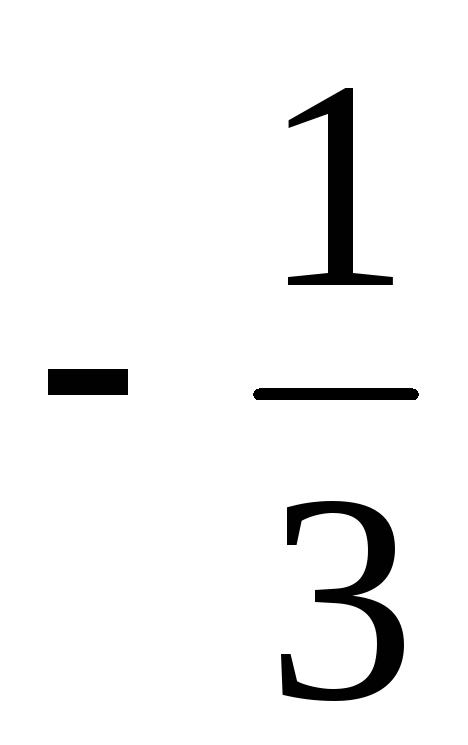Найдем (a,
a):
(a,
a) =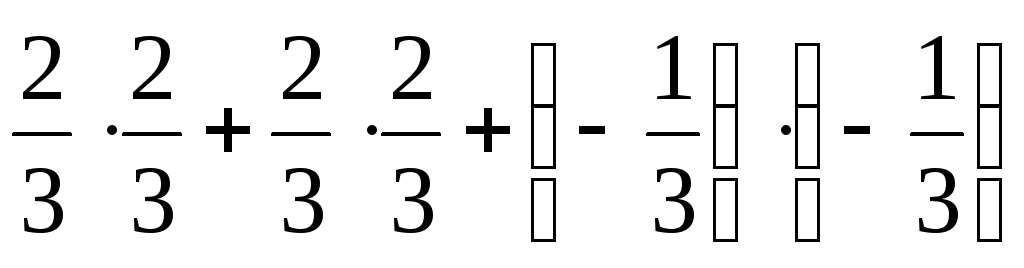 
= 1
||a|| = 1.Нормировать вектор b = (–4, 2, 2, –1). Найдем норму вектора ||b||: (b, b) = (–4)2 + 22 + 22 + (–1)2 = 25 ||b|| =
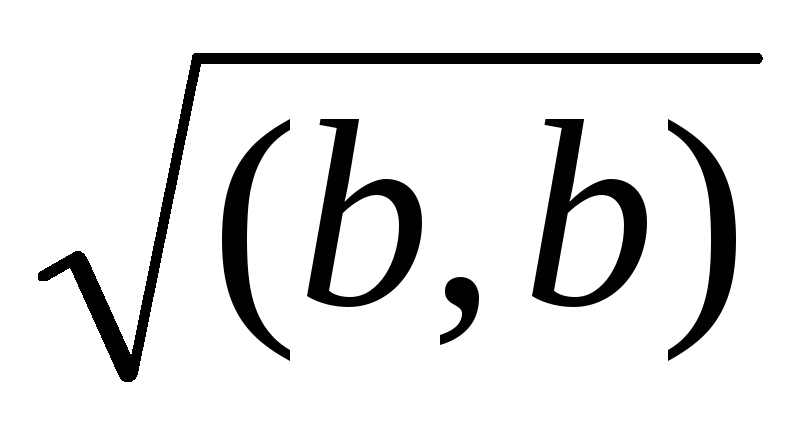= 5.
Вектор e =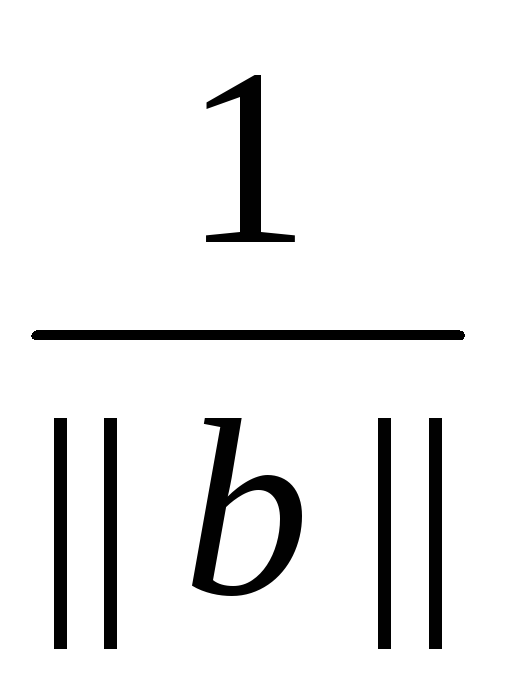 
b
нормирован, это можно проверить,
используя свойство 2, тогда e = 
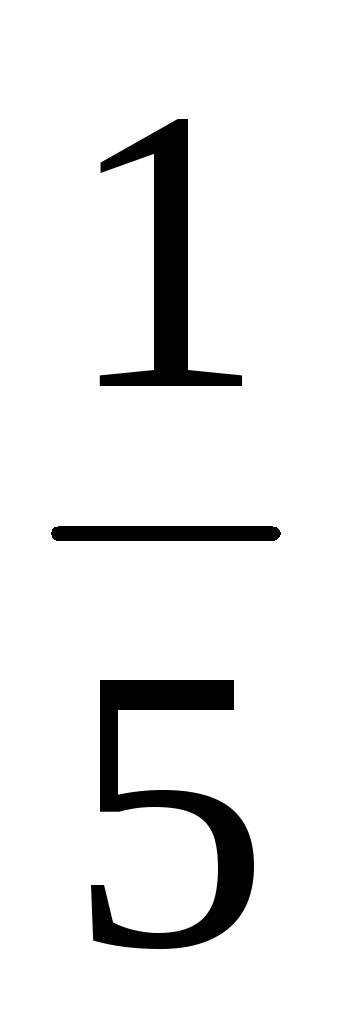b = (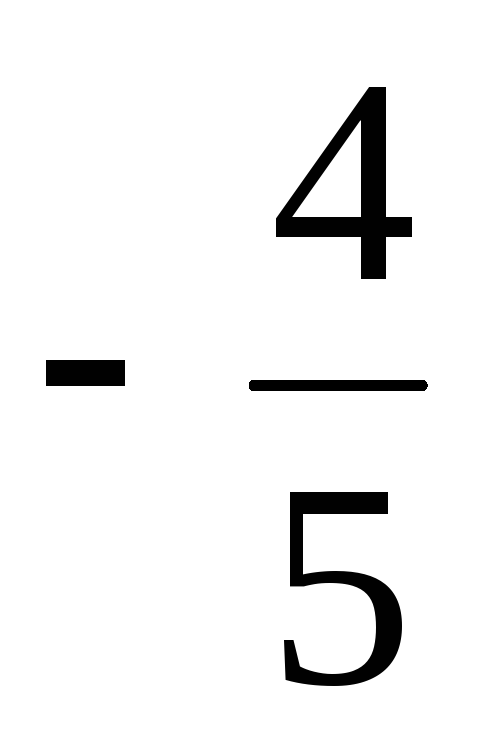
,
,
,
).
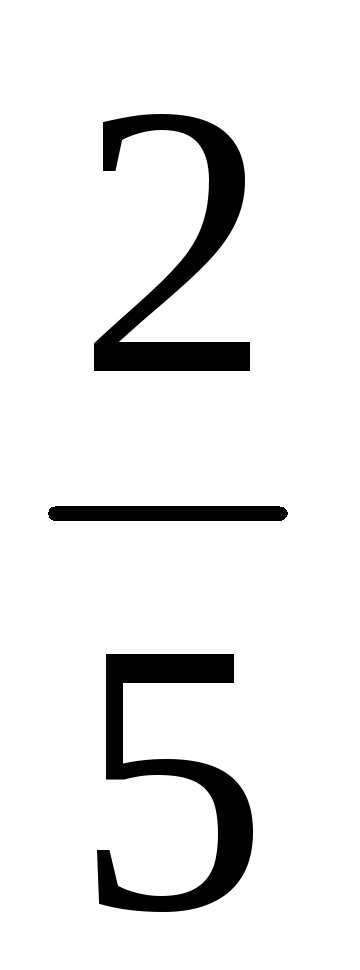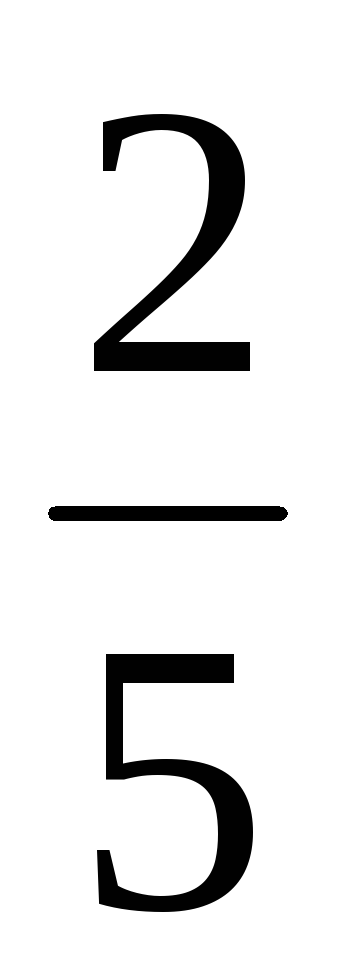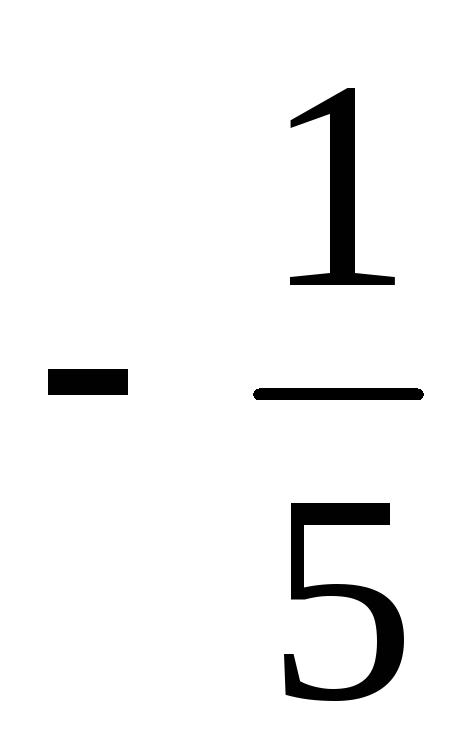Определение 8.18.
Углом
между ненулевыми векторами а
и b
называется
угол, меняющийся в пределах от 0 до
и определенный условием
.
В
силу неравенства Коши – Буняковского
принимает
значения от (–1) до 1 и, следовательно,
угол между ненулевыми векторами
определен.
Определение 8.19. Векторы а и b называются ортогональными, если их скалярное произведение равно нулю. Обозначение: а b.
Это определение согласуется с определением угла между векторами.
Определение 8.20. Нулевой вектор считается ортогональным любому вектору.
Ортонормированный базис евклидова векторного пространства
Определение 8.21. Базис евклидова векторного пространства называется ортогональным, если векторы базиса попарно ортогональны, то есть если а1, а2, …, аn – ортогональный базис пространства, то (аi, аj) = 0 при i ≠ j, i, j = 1, 2, …, n.
Определение 8.22. Ортогональный базис называется ортонормированным, если каждый вектор базиса нормирован, то есть если e1, e2, …, en – ортонормированный базис, то (ei, ej) = 0 при i ≠ j и (ei, ei) = 1, i, j = 1, 2, …, n.
Докажем возможность существования ортонормированного базиса.
Теорема 8.11. Ортогональная система ненулевых векторов линейно независима.
Доказательство. Пусть система векторов а1, а2, …, аk – ненулевая и ортогональная, то есть аi ≠ о, (аi, аj) = 0 при i ≠ j, i, j = 1, 2, …, k. Покажем, что равенство 1а1 + 2а2 + … + kаk = о возможно лишь тогда, когда 1 = 2 = … = k = 0. Умножим это равенство скалярно на а1:
(1а1 + 2а2 + … + kаk, а1) = (о, а1)
1(а1, а1) + 2(а2, а1) + … + k(аk, а1) = 0.
В силу ортогональности системы (т. е. (а2, а1) = 0, …, (аk, а1) = 0) получим 1(а1, а1) = 0 и, так как а1 ≠ о (т. е. (а1, а1) ≠ 0), то 1 = 0. Аналогично доказывается, что 2 = 0, …, k = 0 (умножая исходное равенство по очереди на 2, 3, …, k), следовательно, система векторов а1, а2, …, аk линейно независима. Теорема доказана.