Файл: Линейная Алгебра от 2 октября 2013.doc

Пусть S – разбиение непустого множества А и R_S – бинарное отношение, определяемое следующим образом: (x, y)  R_S тогда и только тогда, когда x и y принадлежат одному и тому же подмножеству семейства S.

Теорема 2.2. Отношение R_S, соответствующее разбиению S непустого множества А, является отношением эквивалентности на А, причем фактор-множество А/R_S совпадает с разбиением S.

Доказательство. 1. Так как S есть разбиение, то  a  А,  М_i  S : a  М_i. Следовательно, по определению отношения R_S, (а, а)  R_S, а значит R_S – рефлексивно.

2. Пусть a, b – произвольные элементы из А такие, что (а, b)  R_S. Тогда, по определению отношения R_S,  М_j  S : a, b  М_j. Следовательно, (b, a)  R_S. Получили, что R_S – симметрично.

3. Пусть a, b, c – произвольные элементы из А такие, что (а, b)  R_S и (b, c)  R_S. Следовательно, по определению отношения R_S,  M_i, M_j S: a, b  M_i и b, c  M_j. Отсюда b  M_i  M_j. Но тогда, по определению разбиения, M_i= M_j , а значит, a, c  M_i , и, по определению отношения R_S, (a, c)  R_S. Получили, что R_S – транзитивно.

Из п. 1 – 3 следует, что R_S – отношение эквивалентности. Фактор-множество A/R_S совпадает с разбиением S по определению отношения R_S.

Замечание 2.2. Частным случаем отношения эквивалентности  является отношение равенства элементов некоторого множества А, которое определяет разбиение множества на одноэлементные классы эквивалентности:  x  A, x/ = {x}. В этом случае классов эквивалентности оказывается столько же, сколько элементов содержится в множестве А, так как каждый элемент из А эквивалентен только самому себе.

В другом частном случае все элементы множества А эквивалентны друг другу. При этом фактор-множество А/ состоит всего из одного класса – самого множества А.

В любом другом случае среди классов эквивалентности имеется хотя бы один класс, который содержит больше одного элемента и в то же время не совпадает с самим множеством А.

Замечание 2.3. Понятие отношения эквивалентности имеет большое значение в математике. Дело в том, что элементы, входящие в один класс эквивалентности неразличимы с точки зрения рассматриваемого отношения эквивалентности. Поэтому считают, что класс эквивалентности определяется любым своим представителем (произвольным элементом этого класса). Это позволяет вместо всех элементов множества изучать совокупность представителей каждого класса эквивалентности. Свойства, которыми обладают все элементы некоторого класса эквивалентности, изучаются на одном его представителе.

Отношения эквивалентности играют важную роль в определении математических понятий.

2.4. Функции

Определение 2.20. Бинарное отношение ƒ Í A ´ B называется функцией из множества A в множество B, если для любого x Î A существует единственный элемент y Î B такой, что (x, y) Î ƒ. При этом элемент y обозначается через ƒ(x) и называется значением функции ƒ для аргумента x. Функция f из A в B обозначается через ƒ: A → B или A B. Если (x, y) Î ƒ, то используется общепринятая запись y = ƒ(x), а также запись ƒ: x y (означает, что функция ƒ ставит в соответствие элементу x элемент y).

Область определения и область значений функции, равные функции определяются так же, как и для бинарных отношений.

Аргументами функции могут являться элементы произвольной природы, в частности, кортежи длины n (x₁, x₂, …, x_n). Функцию ƒ: Aⁿ → B называют n-местной функцией из A в B. Тогда пишут y = ƒ(x₁, x₂, …, x_n) и говорят, что y есть значение функции ƒ при значении аргументов x₁, x₂, …, x_n.

Функции называются также отображениями. Пусть ƒ – функция из A в B. Если A = Domƒ и Imƒ Í B, то говорят, что ƒ есть отображение множества A в множество B. Если A = Domƒ и B = Imƒ, то говорят, что ƒ есть отображение множества A на множество B.

Определение 2.21. Функция ƒ Í A ´ B называется инъективной, или инъекцией, если " x, y Î A, ƒ(x) = ƒ(y) Þ x = y.

Определение 2.22. Функция ƒ Í A ´ B называется сюръективной, или сюръекцией, если для каждого элемента y Î B существует хотя бы один элемент x Î A такой, что y = ƒ(x).

Заметим, что сюръективная функция ƒ Í A ´ B является отображением A на B.

Определение 2.23. Функция ƒ Í A ´ B называется биективной (биекцией) или взаимно однозначным соответствием между множествами A и B, если она одновременно инъективна и сюръективна.

Определение 2.24. Если соответствие, обратное к функции ƒ Í A ´ B, является функциональным и полностью определенным, то оно называется функцией, обратной к ƒ и обозначается ƒ^–1.

Так как в обратном соответствии образы и прообразы меняются местами, то для существования функции, обратной к функции f Í A ´ B, необходимо и достаточно, чтобы Imf = B и каждый элемент y Î Imf имел единственный прообраз.

Утверждение 2.3. Для функции ƒ: A → B существует обратная к ней функция ƒ^–1: B → A тогда и только тогда, когда ƒ – биекция.

Определение 2.25. Пусть даны функции ƒ: A → B и g: B → C. Функция h: A → C называется композицией (суперпозицией) функций f и g, если " x Î A, h(x) = g(f(x)).

Композиция функций f и g обозначается через g _° f, при этом знак _°часто опускается.

3. Матрицы и действия над ними

3.1. Общие понятия

Определение 3.1. Матрицей называется прямоугольная таблица из чисел, содержащая m строк и n столбцов. Числа m и n называют порядком (или типом, или размерностью) матрицы; обозначают m  n или (m, n).

Матрицы обозначаются прописными буквами латинского алфавита: А, В, С, …, а числа, их составляющие – элементы матрицы – строчными буквами с двумя индексами: a_ij, где i – номер строки, j – номер столбца.

Например, матрица размерности m  n имеет вид:

А = ,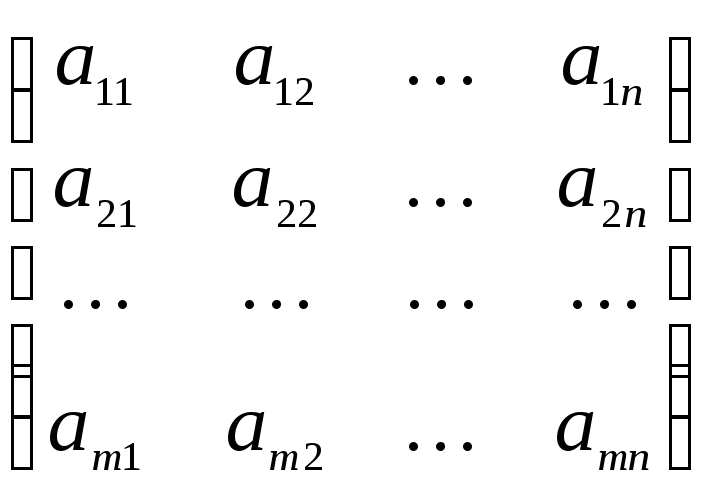

коротко записывают А = ||a_ij|| или А = (a_ij), где i = 1, 2, …, m, j = 1, 2, …, n.

Пусть В = 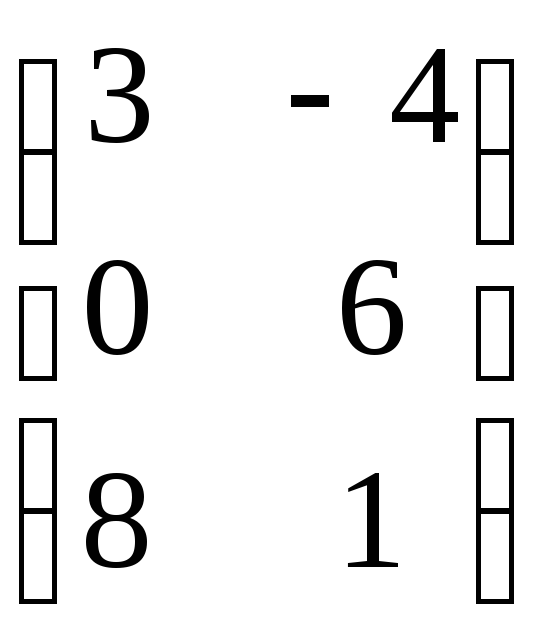– конкретная матрица размерности 3  2, тогда пишут В₃_₂.

Определение 3.2. Матрица называется квадратной порядка n, если число строк равно числу столбцов и равно n (то есть m = n).

Определение 3.3. Две матрицы А = (a_ij) и B = (b_ij) называются однотипными, если они имеют одинаковое число строк и одинаковое число столбцов.

Определение 3.4. Две однотипные матрицы А = (a_ij) и B = (b_ij) называют равными и пишут А = B, если a_ij = b_ij для любых индексов i, j.

Определение 3.5. Матрица, состоящая из одной строки, называется матрицей-строкой или вектором-строкой.

Определение 3.6. Матрица, состоящая из одного столбца, называется матрицей-столбцом или вектором-столбцом.

Например, матрица-строка А₁_₃ = (–2 5 1), матрица-столбец В₃_₁ = .

В квадратных матрицах А = (a_ij) порядка n вводится понятие главной диагонали: a₁₁, a₂₂, …, a_nn и побочной диагонали: a₁_n, a₂_n_–1, …, a_n₁.

Определение 3.7. Квадратная матрица, все элементы которой вне главной диагонали равны нулю называется диагональной, т. е. матрица вида

Определение 3.8. Квадратная матрица вида 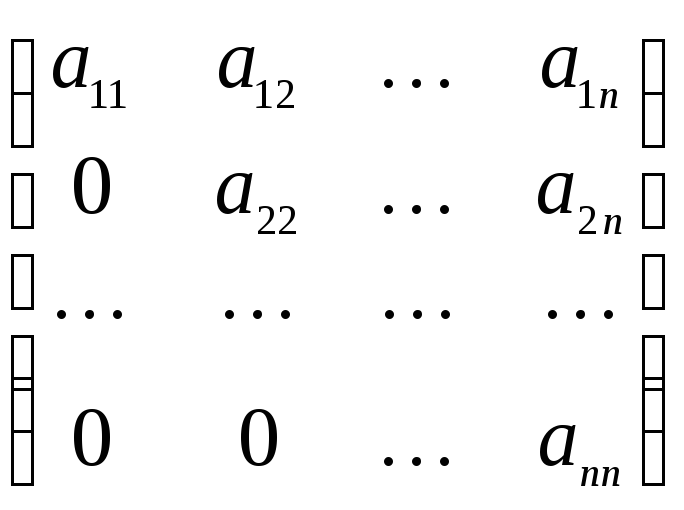называется верхнетреугольной. Аналогично вводится понятие нижнетреугольной матрицы.

Определение 3.9. Квадратная матрица, у которой все элементы главной диагонали равны единице, а все остальные элементы равны нулю, называется единичной матрицей порядка n, т. е. E = .