Файл: Линейная Алгебра от 2 октября 2013.doc

1) A = . Для этого случая собственные векторы уже найдены (пример 9.7), линейно независимых векторов оказалось только 2, а в базисе должно быть 3. Вывод: матрица A к диагональному виду не приводится. Другими словами: матрица A не подобна диагональной.

2) A = 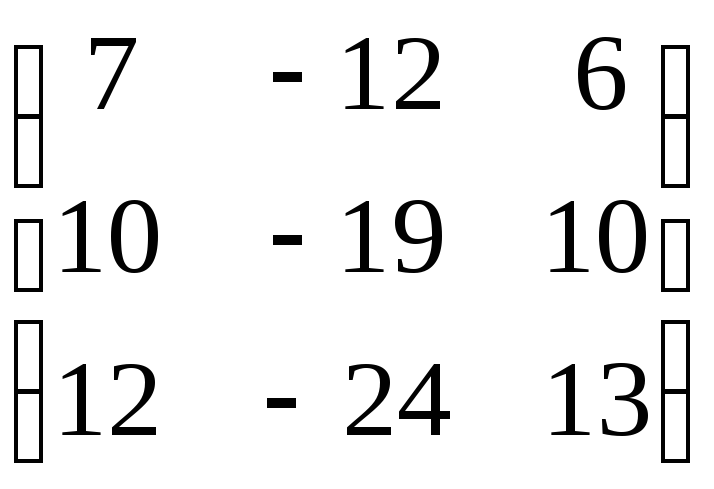. Находим собственные значения матрицы A. Вычислим определитель

|A – E| = = =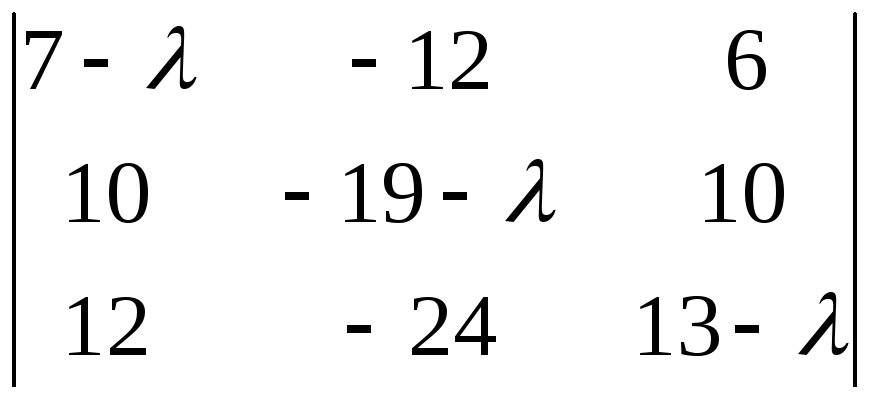

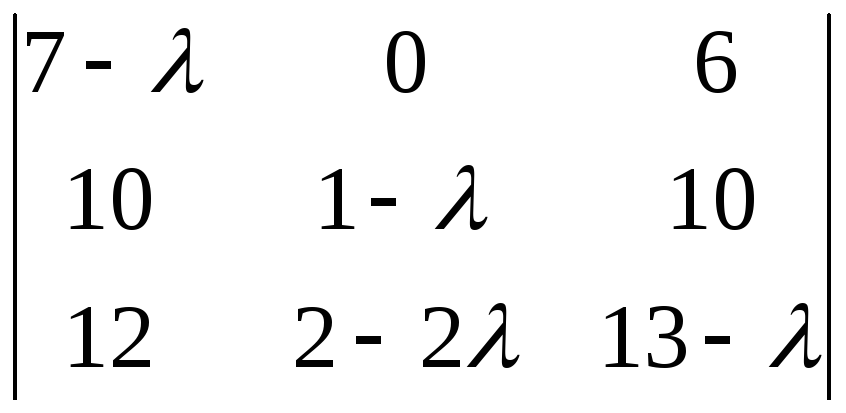=(1 – 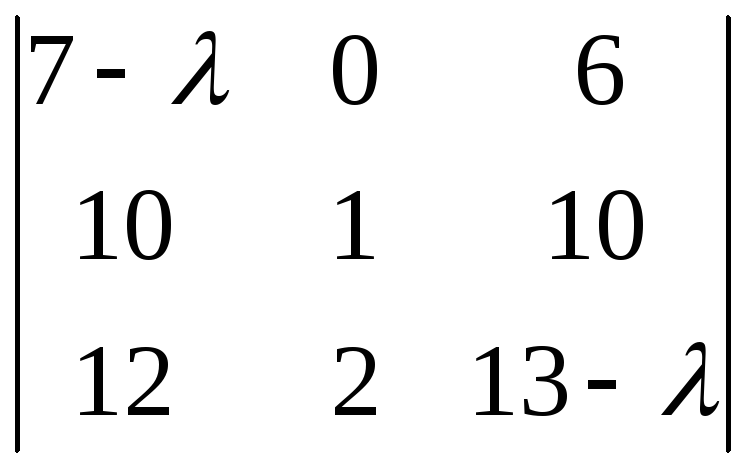) = (1 – )=

= (1 – )1(–1)²⁺²= (1 – )((7 – )(–7 – ) – 6(–8)) =

= (1 – )(² – 1) = –( + 1)( – 1)² = 0. Тогда ₁ = ₂ = 1, ₃ = –1 – собственные значения матрицы A.

Находим собственные векторы, соответствующие этим собственным значениям. Рассмотрим случай ₁ = ₂ = 1. Решаем однородную систему линейных уравнений  (1 –2 1), тогда х₁ = 2х₂ – х₃ –общее решение системы, векторы с₁ = (2, 1, 0) с₂ = (1, 0, –1) линейно независимые собственные векторы с собственным значением ₁ = ₂ = 1.

Рассмотрим случай ₃ = –1. Получаем систему . Решая ее, получим только один линейно независимый собственный вектор с₃ = (3, 5, 6).

Найдены три линейно независимых собственных вектора с₁, с₂, с₃. Выберем их в качестве нового базиса и найдем матрицу линейного оператора в этом базисе.

Поскольку (с₁) = 1с₁, (с₂) = 1с₂, (с₃) = (–1)с₃, то матрица линейного оператора M'() = и T = 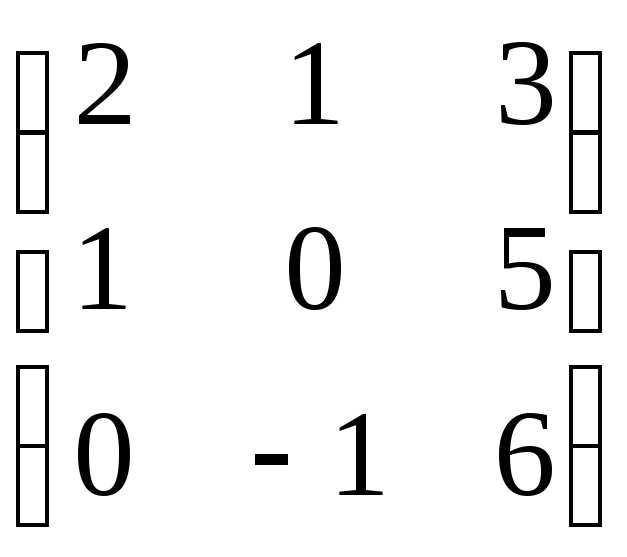–матрица перехода от старого базиса к новому.

10. Жорданова нормальная форма матрицы линейного оператора

10.1. Понятие λ-матрицы

Известно, что матрица линейного оператора в базисе из собственных векторов приводится к диагональному виду. Однако над множеством действительных чисел линейный оператор может не иметь собственных значений, а значит и собственных векторов. Над множеством комплексных чисел любой линейный оператор имеет собственные векторы, но их может быть недостаточно для базиса. Есть другая каноническая форма матрицы линейного оператора, к которой можно привести любую матрицу над множеством комплексных чисел.

Теорема 10.1. Всякая матрица с комплексными элементами приводится во множестве комплексных чисел C к жордановой^¹⁴ нормальной форме.

Дадим необходимые определения:

Определение 10.1. Квадратная матрица порядка n, элементами которой служат многочлены произвольной степени от переменной λ с коэффициентами из множества комплексных чисел C, называется λ-матрицей (или многочленной матрицей, или полиномиальной матрицей).

Примером многочленной матрицы служит характеристическая матрица A – λE произвольной квадратной матрицы A. На главной диагонали стоят многочлены первой степени, вне ее – многочлены нулевой степени или нули. Обозначим такую матрицу как A(λ).

Пример 10.1. Пусть дана матрица A = , тогда A – λE = = 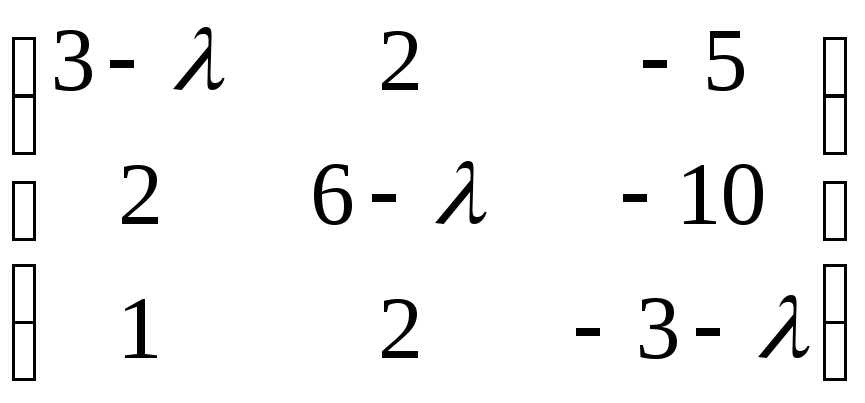= A(λ).

Определение 10.2. Элементарными преобразованиями λ-матрицы называют следующие преобразования:

умножение любой строки (столбца) матрицы A(λ) на любое число, не равное нулю;
прибавление к любой i-той строке (i-ому столбцу) матрицы A(λ) любой другой j-ой строки (j-ого столбца), умноженной на произвольный многочлен ().

Свойства λ-матрицы

1) С помощью этих преобразований в матрице A(λ) можно переставить любые две строки или любые два столбца.

2) С помощью этих преобразований в диагональной матрице A(λ) можно менять местами диагональные элементы.

Пример 10.2. 1)     .

2)   .

Определение 10.3. Матрицы A(λ) и B(λ) называются эквивалентными, если от A(λ) можно перейти к B(λ) при помощи конечного числа элементарных преобразований.

Задача заключается в том, чтобы по возможности упростить матрицу A(λ).

Определение 10.4. Канонической λ-матрицей называется λ-матрица, обладающая следующими свойствами:

матрица A(λ) диагональная;
всякий многочлен е_i(), i = 1, 2, …, n нацело делится на е_i_–1();
старший коэффициент каждого многочлена е_i(), i = 1, 2, …, n равен 1, или этот многочлен равен нулю.

A(λ) = .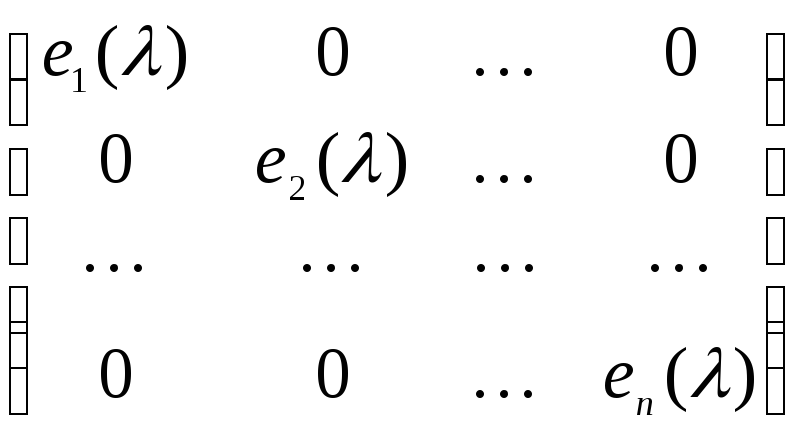

Замечание. Если среди многочленов е_i() встречаются нули, то они занимают на главной диагонали последние места (по свойству 2), если есть многочлены нулевой степени, то они равны 1 и занимают на главной диагонали первые места.

Нулевая и единичная матрицы являются каноническими λ-матрицами.

Теорема 10.2. Всякая λ-матрица эквивалентна некоторой канонической λ-матрице (то есть она приводится элементарными преобразованиями к каноническому виду)

Пример 10.3. Привести матрицу A(λ) = 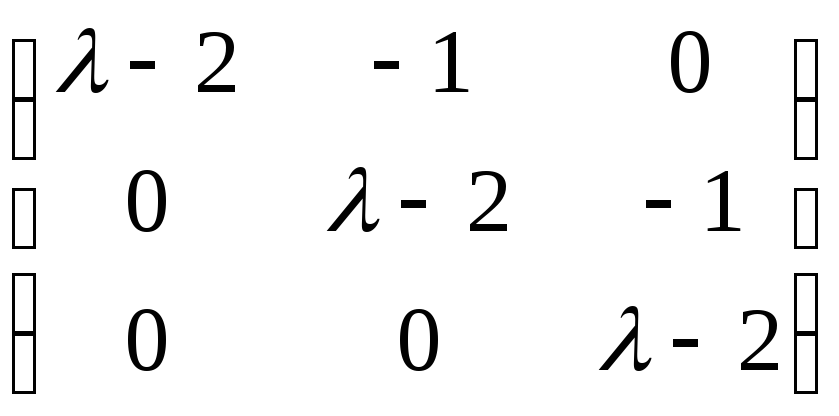к каноническому виду.

Решение. Ход преобразований аналогичен преобразованиям в методе Гаусса, при этом левый верхний элемент матрицы при приведении ее к каноническому виду отличен от нуля и имеет наименьшую степень.

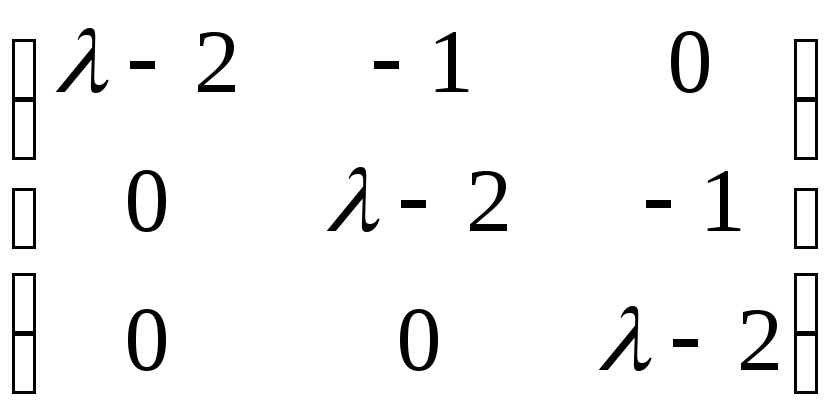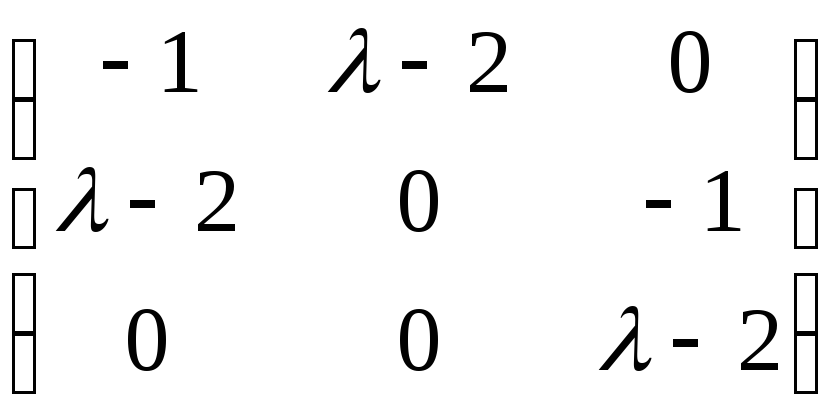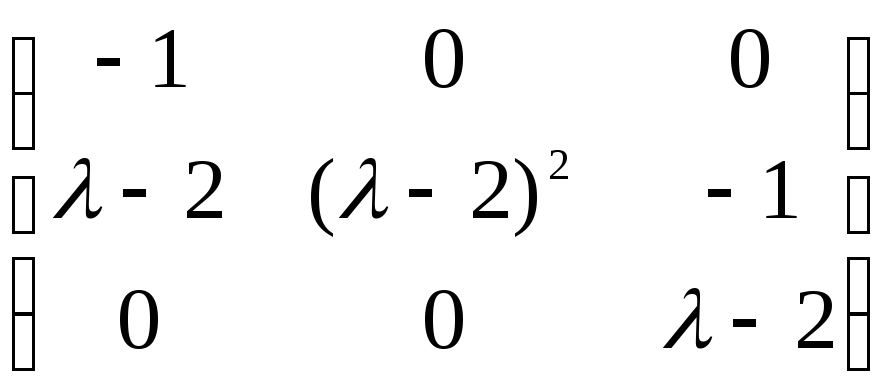
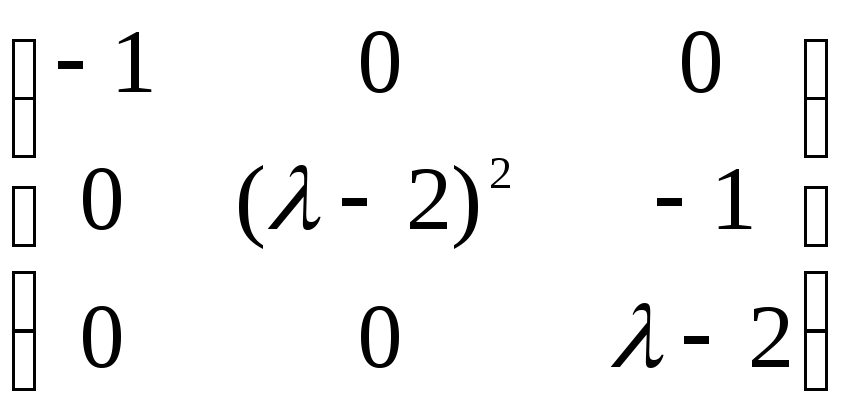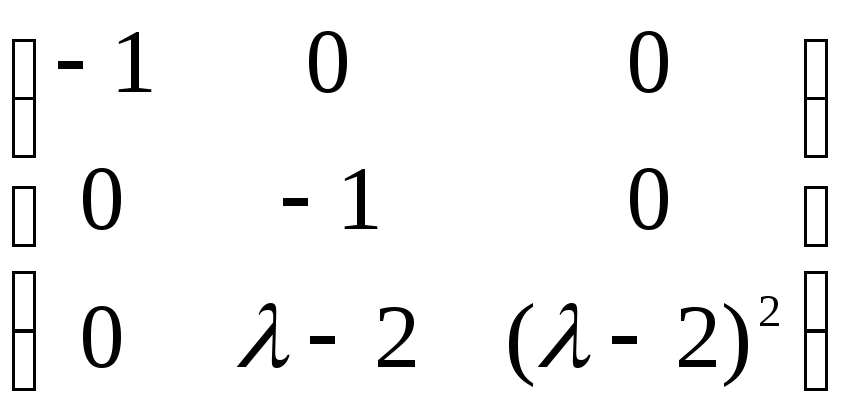
A(λ) =  (меняем местами первый и второй столбцы)   (к второму столбцу прибавляем первый столбец, умноженный на ( – 2))   (ко второй строке прибавляем первую строку, умноженную на ( – 2))   (меняем местами второй и третий столбцы)   (к третьему столбцу прибавляем второй столбец умноженный на ( – 2)³)   (к третьей строке прибавляем вторую строку, умноженную на ( – 2))  .
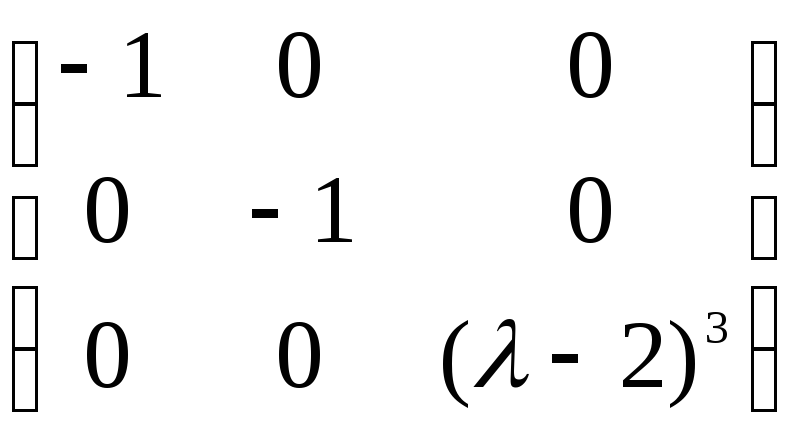