ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 11.08.2024
Просмотров: 543
Скачиваний: 0
СОДЕРЖАНИЕ
Т. Н. Матыцина е. К. Коржевина линейная алгебра
1.1. Множества и их элементы. Способы задания множеств
1.2. Подмножества. Диаграммы Эйлера – Венна
1.3. Операции над множествами и их свойства
2. Пересечение (или произведение).
4. Декартовое произведение (или прямое произведение).
Свойства операций над множествами
1.4. Метод математической индукции
Операции над комплексными числами
Геометрическая интерпретация комплексных чисел
Тригонометрическая форма комплексного числа
Действия над комплексными числами в тригонометрической форме
4. Извлечение корня n-ой степени.
Показательная форма комплексного числа
Способы задания бинарных отношений
Операции над бинарными отношениями
2.2. Свойства бинарных отношений
2.3. Отношение эквивалентности
3. Матрицы и действия над ними
3.2. Основные операции над матрицами и их свойства
3.2.1. Сложение однотипных матриц
3.2.2. Умножение матрицы на число
4. Определители квадратных матриц
4.1. Определители матриц второго и третьего порядка
4.2. Определитель матрицы n-го порядка
4.4. Практическое вычисление определителей
5. Ранг матрицы. Обратная матрица
5.2. Нахождение ранга матрицы методом окаймления миноров
5.3. Нахождение ранга матрицы с помощью элементарных преобразований
5.4. Понятие обратной матрицы и способы ее нахождения
Алгоритм нахождения обратной матрицы
Нахождение обратной матрицы с помощью элементарных преобразований
6.1. Основные понятия и определения
6.2. Методы решения систем линейных уравнений
6.3. Исследование системы линейных уравнений
6.4. Однородные системы линейных уравнений
Свойства решений однородной системы линейных уравнений
Фундаментальный набор решений однородной системы линейных уравнений
7. Арифметическое n-мерное векторное пространство
7.2. Линейная зависимость и независимость системы векторов
Свойства линейной зависимости системы векторов
Две теоремы о линейной зависимости
7.3. Базис и ранг системы векторов
8. Векторные (линейные) пространства
8.1. Определение векторного пространства над произвольным полем.
Простейшие свойства векторных пространств
Линейная зависимость и независимость системы векторов
8.2. Подпространства. Линейные многообразия
Пересечение и сумма подпространств
8.3. Базис и размерность векторного пространства
8.3.1. Конечномерные векторные пространства
Базис конечномерного векторного пространства
8.3.2. Базисы и размерности подпространств
8.3.3. Координаты вектора относительно данного базиса
8.3.4. Координаты вектора в различных базисах
8.4 Евклидовы векторные пространства
Скалярное произведение в координатах
Скалярное произведение в ортонормированном базисе
Ортогональное дополнение подпространства
9.1. Основные понятия и способы задания линейных операторов
Способы задания линейных операторов
9.2. Матрица линейного оператора Связь между координатами вектора и координатами его образа
Матрицы линейного оператора в различных базисах
Свойства отношения подобия матриц
9.4. Действия над линейными операторами
1. Сложение линейных операторов.
Свойства сложения линейных операторов
9.5. Ядро и образ линейного оператора
9.6. Обратимые линейные операторы
9.7. Собственные векторы линейного оператора
9.7.1. Свойства собственных векторов
9.7.2. Характеристический многочлен матрицы
9.7.3. Нахождение собственных векторов линейного оператора
9.7.4. Алгоритм нахождения собственных векторов линейного оператора
9.7.5.Условия, при которых матрица подобна диагональной матрице
10. Жорданова нормальная форма матрицы линейного оператора
10.2. Жорданова нормальная форма
10.3.Приведение матрицы к жордановой (нормальной) форме
Алгоритм приведения матрицы a к жордановой форме
11. Билинейные и квадратичные формы
Преобразование матрицы билинейной формы при переходе к новому базису. Ранг билинейной формы
Приведение квадратичной формы к каноническому виду
Закон инерции квадратичных форм
Классификация квадратичных форм
Необходимое и достаточное условие знакоопределенности квадратичной формы
Необходимое и достаточное условие знакопеременности квадратичной формы
Необходимое и достаточное условие квазизнакопеременности квадратичной формы
Критерий Сильвестра знакоопределенности квадратичной формы
Пусть форма A(x, x) в базисе e = {e1, e2, …, en} определяется матрицей A(e) = (aij),
A(x,
x) = 
,
и пусть 1 = а11,
2 = 
,
…, n =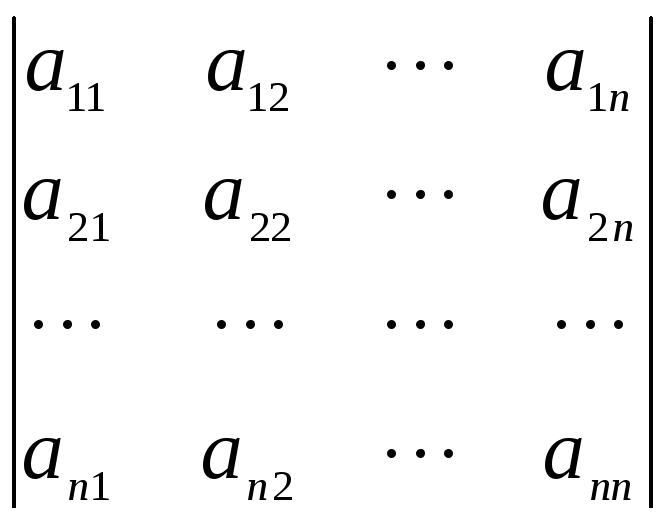 
угловые миноры и определители матрицы
(aij).
Тогда справедливо утверждение:
Теорема 11.4 (критерий Сильвестра).
Для того чтобы квадратичная форма A(x, x) была положительно определенной, необходимо и достаточно, чтобы были выполнены неравенства: 1 > 0, 2 > 0, …, n > 0.
Для того чтобы квадратичная форма A(x, x) была отрицательно определенной, необходимо и достаточно, чтобы знаки угловых миноров чередовались, причем 1 < 0.
Пример 11.2.
Выяснить, является ли квадратичная
форма A(x, x) = 5
+ 
+ 5x3 + 4x1x2 – 8x1x3 – 4x2x3
положительно определенной?
Решение. Составим матрицу этой квадратичной формы:
M = 
Вычислим ее угловые миноры:
1 = 5 > 0,
2 = 
= 5 – 4 = 1 > 0,
3 =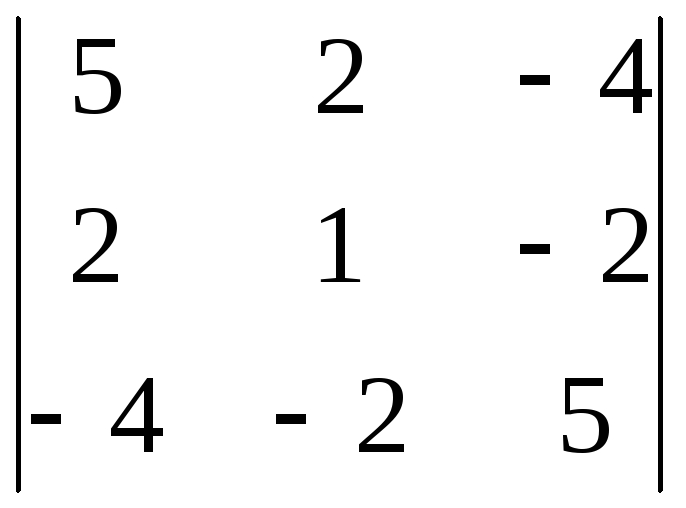 
= 25 + 16 + 16 – 16 – 20 – 20 = 1 > 0.
Все угловые миноры положительны, следовательно, квадратичная форма положительно определенна.
Пример 11.3.
Выяснить, является ли квадратичная
форма A(x, x) = 3
+ 
+ 5x3 + 4x1x2 – 8x1x3 – 4x2x3
положительно определенной?
Решение. Составим матрицу этой квадратичной формы:
M =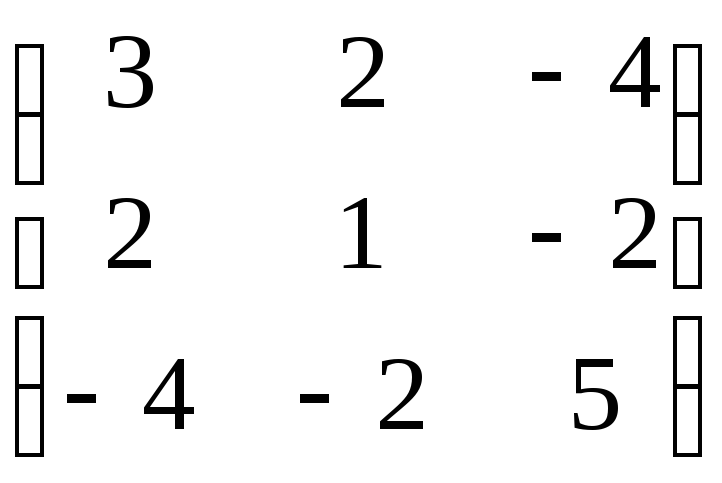 
Вычислим ее угловые миноры:
1 = 3 > 0,
2 = 
= 3 – 4 = –1 < 0,
3 =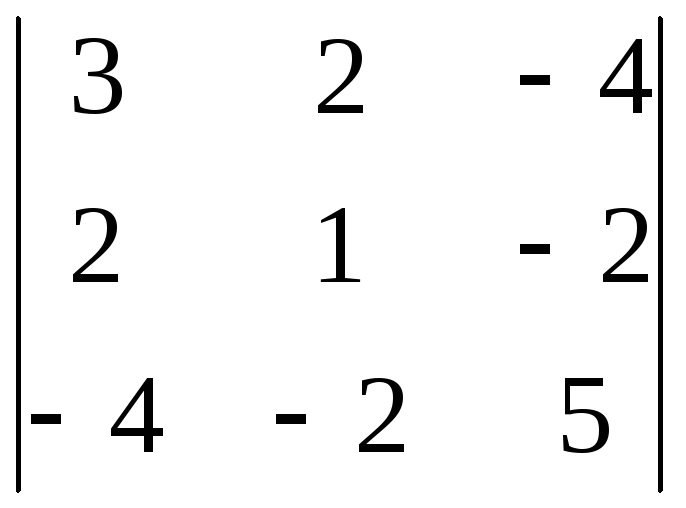 
= 15 + 16 + 16 – 16 – 12 – 20 = –1 < 0.
Вывод. Квадратичная форма A(x, x) не является положительно определенной, т. к. 2 < 0, и отрицательно определенной не является, т. к. 1 > 0, т.о. она знакопеременная.
Заключение
Линейная алгебра является обязательной частью любой программы по высшей математике. Любой другой раздел предполагает наличие знаний, умений и навыков, заложенных во время преподавания этой дисциплины. Данной пособие в доступной, но математически строгой форме, дает возможность освоить все основные понятия и ознакомить с типовыми упражнениями.
Предполагается выпуск задачника по линейной алгебре дополняющего данное пособие. В задачник войдут материалы для проведения практических занятий; заданий для домашних работ, а также практикумы с индивидуальными заданиями для самостоятельного решения.
Библиографический список
Бурмистрова Е.Б., Лобанов С.Г. Линейная алгебра с элементами аналитической геометрии. – М.: Изд-во ВШЭ, 2007.
Беклемишев Д.В. Курс аналитической геометрии и линейной алгебры. – М.: Наука, 2006.
Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. Часть I. – М.: ОНИКС 21 век, Мир и образование, 2003.
Ермаков В.И. Сборник задач по высшей математике для экономистов. – М.: Инфра - М, 2009.
Ермаков В.И. Общий курс высшей математики для экономистов. – М.: Инфра - М, 1999.
Ильин В.А., Позняк Э.Г. Линейная алгебра. – М.: Наука, 2002.
Кремер Н.Ш. Высшая математика для экономистов. – М.: Юнити, 2004.
Кудрявцев В.А., Демидович Б.П. Краткий курс высшей математики. – М.: Наука, 1989.
Крамор В. С. Алгебра и начало анализа / В. С. Крамор. – М.: Высш. школа, 1981.
Куликов Л. Я. Алгебра и теория чисел: учеб. пособие для педагогических институтов / Л. Я. Куликов. – М.: Высш. школа, 1979.
Куликов Л. Я. Сборник задач по алгебре и теории чисел / Л. Я. Куликов, А. И. Москаленко, А. А. Фомин. – М.: Просвещение, 1993.
Лунгу К. Н. Сборник задач по высшей математике / К. Н. Лунгу. – М.: Айрис-пресс, 2007.
Малыкин В.И. Математика в экономике. – М.: Инфра - М, 2002.
Солодовников А.С., Бабайцев В.А., Браилов А.В. Математика в экономике. Часть I. – М.: Финансы и кредит, 2000.
Фадеев Д.К., Соминский И.С. Задачи по высшей алгебре. – СПб.: Лань, 2001.
Чередникова А. В. Дискретная математика. Теория и практика / А. В. Чередникова, О. Б. Садовская, Л. А. Каминская. – Кострома: Изд-во Костром. гос. технол. ун-та, 2011.
Шапорев С. Д. Дискретная математика. Курс лекций и практических занятий / С. Д. Шапорев. – СПб.: БХВ-Петербург, 2007. – 400с.
Шепелев Ю. П. Дискретная математика: учеб. пособие / Ю. П. Шепелев. – СПб.: Лань, 2008.
Математический энциклопедический словарь / гл. ред. Ю. В. Прохоров; ред. кол.: С. И. Адян, Н. С. Бахвалов, В. И. Битюцков, А. П. Ершов, Л. Д. Кудрявцев, А. Л. Онищик, А. П. Юшкевич. – М.: Сов. энциклопедия, 1988.
Учебное издание
Матыцина Татьяна Николаевна
Коржевина Елена Константиновна
Линейная алгебра
Учебно-методическое пособие
Редактор и корректор Г. Д. Неганова
Компьютерный набор Т. Н. Матыциной, Е. К. Коржевина
Подписано в печать 01.04.2013.
Формат 60х90/16.
Уч.-изд. л. 4,0.
Тираж 100 экз.
Изд. № 26.
Костромской государственный университет имени Н. А. Некрасова
156961, Г. Кострома, ул. 1 Мая, 14
1 Георг Кантор (1845–1918) – немецкий математик.
2 Леонард Эйлер (1707–1783) – швейцарский, немецкий и российский математик и механик.
3 Джон Венн (1834–1923) – английский логик и философ.
4 Огастес (Август) де Морган (1806–1871) – шотланский математик и логик.
5 Джероламо Кардано (1501–1576) – итальянский математик, инженер, философ, медик и астролог.
6 Иоганн Карл Фридрих Гаусс (1777–1855) – немецкий математик, механик, физик и астроном.
7 Каспар Вессель (1745–1818) – датско-норвежский математик.
8 Жан Робер Арган (1768 – 1822) – непрофессиональный математик.
9 Абрахам де Муавр (1667–1754) – английский математик.
10 Пьер Фредерик Саррюс (1798–1861) – французский математик.
11 Габриэль Крамер (1704–1752) – швейцарский математик.
12 Леопольд Кронекер (1823–1891) – немецкий математик.
13 Альфредо Капелли (1855–1910) – итальянский математик.
14Камиль Жордан (1838–1922) – французский математик.
15 Джеймс Джозеф Сильвестр (1814–1897) – английский математик.