Файл: Линейная Алгебра от 2 октября 2013.doc

Доказательство. Обозначим это множество символом L⁽^⁾. Докажем, что множество L⁽^⁾  {o} образует подпространство пространства V, для чего проверим его замкнутость относительно сложения векторов и умножения их на элемент поля.

Пусть x, y  L⁽^⁾  {o}, тогда (x) = х, (y) = y. Найдем (x + y): (x + y) = (x) + (y) = х + y = (х + y), значит (х + y)  L⁽^⁾  {o}.

Пусть x  L⁽^⁾  {o}, k  P, (x) = х, тогда (kx) = k(x) = k(х) = (kх), значит kх  L⁽^⁾  {o}.

4. Собственные векторы с попарно различными собственными значениями линейно независимы.

Следствие. Линейный оператор, заданный в n-мерном линейном пространстве, не может иметь более чем n различных собственных значений.

9.7.2. Характеристический многочлен матрицы

Дана матрица A  Рⁿ^ⁿ (или A  Rⁿ^ⁿ).

Определение 9.14. Характеристическим многочленом матрицы A называется многочлен, зависящий от λ и равный |A – E|, т. е. многочлен f(λ) = |A – E|, где E – единичная матрица таково же порядка что и А.

Пример 9.6. Найти характеристический многочлен матрицы A = .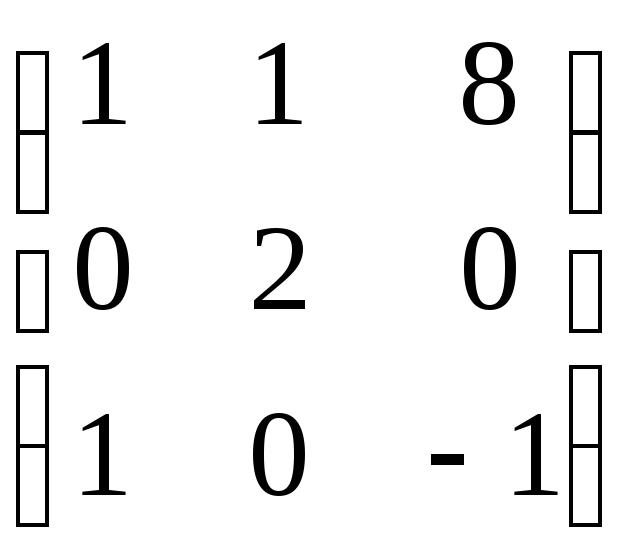

Решение. Составим определитель матрицы A – E и вычислим его

|A – E| = = =

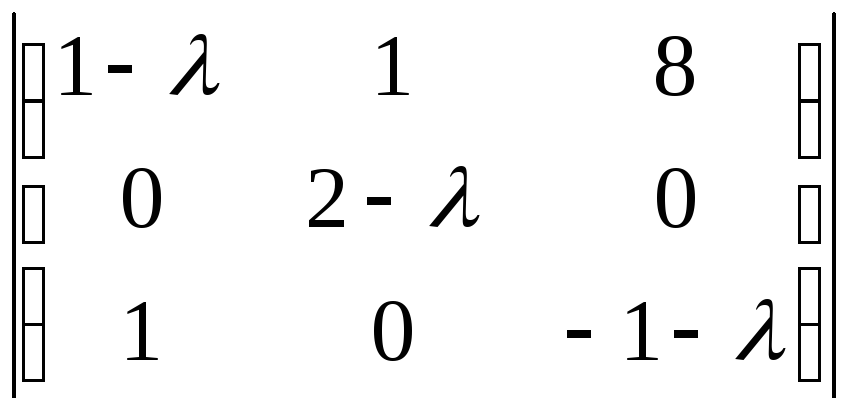= (2 – λ)(–1)²⁺² · = (2 – λ)((1 – )(–1 – ) – 8) =

= (2 – λ)(λ – 3)(λ + 3).

Определение 9.15. Характеристическим уравнением матрицы A называется уравнение |A – E| = 0.

Определение 9.16. Собственными значениями (собственными числами) матрицы A называются корни ее характеристического уравнения.

Найдем собственные значения матрицы из примера 9.6: (2 – λ)(λ – 3)(λ + 3) = 0. Получим: ₁ = 2, ₂ = 3, ₃ = –3.

Теорема 9.12. Характеристические многочлены подобных матриц равны.

Доказательство. Пусть матрицы А и В подобны, то есть А = T^–1ВТ. Тогда

|A – E| = |T^–1ВТ – T^–1ЕТ | = |T^–1(В – Е)Т | = |T^–1||В – Е||Т | = = |T^–1||Т ||В – Е| = |T^–1Т ||В – Е| = |E||В – Е| = 1|В – Е| = |В – Е|.

Так как характеристические многочлены равны, то совпадают и множества собственных значений подобных матриц А и В.

Следствие. Характеристический многочлен матрицы линейного оператора не зависит от базиса, в котором найдена эта матрица (матрицы линейного оператора, найденные в различных базисах, подобны).

9.7.3. Нахождение собственных векторов линейного оператора

Для нахождения собственных векторов линейного оператора надо найти решения уравнения (х) = λx, в котором неизвестными величинами являются собственные значения λ линейного оператора  и ненулевые векторы x.

Для нахождения собственных значений линейного оператора  используется следующая теорема.

Теорема 9.13. Множество собственных значений линейного оператора  совпадает с множеством собственных значений его матрицы.

Доказательство. Пусть λ – собственное значение линейного оператора . Это означает, что существует ненулевой вектор x, такой что (х) = λx. Из этого векторного равенства вытекают следующие матричные равенства:

[(х)] = [λx]  M()[x] = λ[x]  M()[x] – λE[x] = [0] 

(M() – λE)[x] = [0]. ()

Равенство () является матричной формой записи однородной системы линейных уравнений с основной матрицей M() – λE, причем эта система по условию имеет ненулевые решения. Условие существования ненулевых решений – равенство нулю определителя основной матрицы системы, следовательно, выполнятся равенство: |M() – λE| = 0, из которого следует, что λ – собственное значение матрицы M() линейного оператора (х) = λx.

Обратно, пусть λ – собственное значение матрицы M() линейного оператора , то есть |M() – λE| = 0. Из этого равенства следует, что система однородных линейных уравнений () имеет ненулевые решения. Следовательно, существует ненулевой вектор x, такой что (х) = λx и λ – собственное значение линейного оператора .

9.7.4. Алгоритм нахождения собственных векторов линейного оператора

Найти собственные значения линейного оператора как собственные значения его матрицы
Для каждого из найденных собственных значений ₀ находим собственные векторы, решая однородную систему линейных уравнений () с основной матрицей M() – λ₀E.
Множество 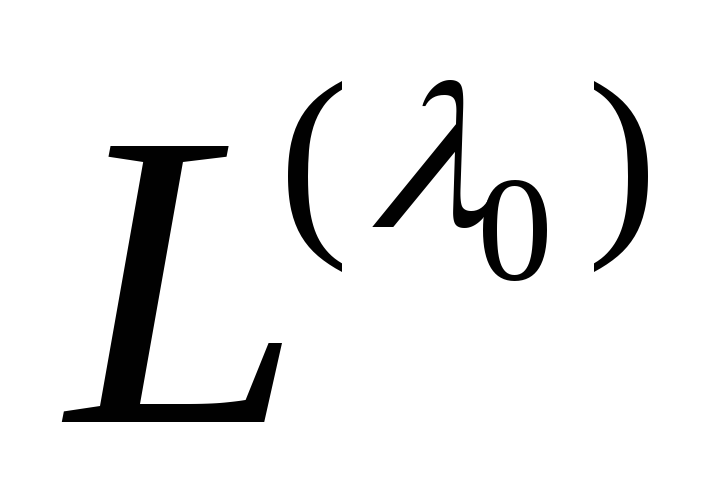равно линейной оболочке фундаментального набора решений этой системы за исключением нулевого вектора.

Пример 9.7. Найти собственные векторы линейного оператора с матрицей M() = .

Решение. Находим собственные значения матрицы линейного оператора, для чего решаем уравнение |M() – λE| = 0.

= (2–)(–1)^3 + 3 = (2 – )((–)(4 – ) – (–4)) =

= (2 – )(² – 4 + 4) = (2 – )( – 2)² = (2 – )³ = 0  ₁ = ₂ = ₃ = 2.

Итак, получили f(λ) = (2 – )³ – характеристический многочлен матрицы M(); (2 – )³ = 0 – характеристическое уравнение матрицы M(); ₁ = ₂ = ₃ = 2 – собственные значения матрицы M(), т. е. это собственные значения линейного оператора .

Собственное значение у этого линейного оператора только одно, поэтому решаем только одну однородную систему линейных уравнений с матрицей .

.

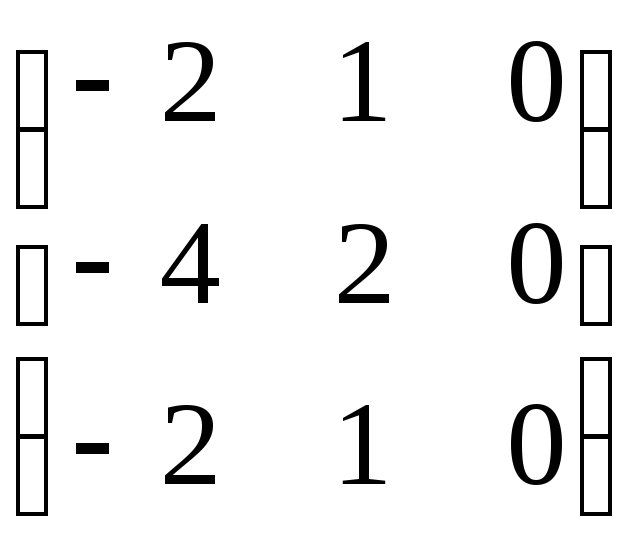
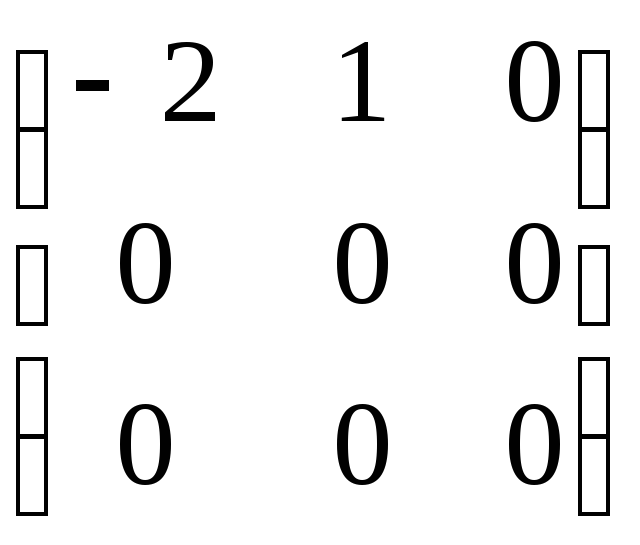
Выпишем общее решение этой системы х₁ = (х₂ + 0х₃) и составим фундаментальный набор решений

	х₁	х₂	х₃
с₁	1	2	0
с₁	0	0	1

с₁ = (1, 2, 0), с₂ = (0, 0, 1).

Ответ. Множество собственных векторов с собственным значением λ = 2 это множество L = L(с₁, с₂)\{o} = {k₁c₁ + k₂c₂, }.

9.7.5.Условия, при которых матрица подобна диагональной матрице

Пусть A – квадратная матрица. Можно считать, что это матрица некоторого линейного оператора, заданного в каком-то базисе. Известно, что в другом базисе матрица линейного оператора примет другой вид, в частности, как в одном из предыдущих примеров 9.3, диагональный. Это значит, что исходная матрица подобна диагональной матрице. Возникает вопрос: всегда ли данная матрица подобна диагональной? Как это установить? Как найти соответствующий базис?

Теорема 9.14. Матрица A подобна диагональной матрице тогда и только тогда, когда линейный оператор , заданный этой матрицей, имеет n линейно независимых собственных векторов.

Доказательство. Пусть матрица A подобна диагональной матрице, то есть у линейного оператора  с матрицей A = M() в некотором базисе с₁, с₂, …, с_n матрица примет следующий вид M'() = . Используя матрицу, найдем образы базисных векторов: (с₁) = ₁с₁, (с₂) = ₂с₂, …, (с_n) = _nс_n. Получены n линейно независимых собственных векторов.

У линейного оператора  есть n линейно независимых собственных векторов с₁, с₂, …, с_n с собственными значениями ₁, ₂, …, _n. Выберем векторы с₁, с₂, …, с_n в качестве базисных векторов и найдем матрицу оператора  в этом базисе. Используя равенства (с₁) = ₁с₁, (с₂) = ₂с₂, …, (с_n) = _nс_n составим матрицу M'(): M'() = .

Теорема 9.15. Если матрица A имеет n попарно различных собственных значений, то она подобна диагональной матрице.

Это утверждение основано на свойстве собственных векторов: попарно различным собственным значениям соответствуют линейно независимые собственные векторы.

Пример 9.8. Привести матрицу A к диагональному виду, если это возможно, указать базис и матрицу перехода.

Смотрите также файлы

Лекция_2.doc

Лекция_1.doc

Лекция.docx

Лекция физиология почек.docx

лекция по терморегуляции.docx

Файл: Линейная Алгебра от 2 октября 2013.doc

9.7.2. Характеристический многочлен матрицы

9.7.3. Нахождение собственных векторов линейного оператора

9.7.4. Алгоритм нахождения собственных векторов линейного оператора

9.7.5.Условия, при которых матрица подобна диагональной матрице

Смотрите также файлы

Информация

Списки файлов

Дополнительно