Файл: Линейная Алгебра от 2 октября 2013.doc

Рассмотрим линейно независимую систему векторов; она совпадает со своей максимальной линейно независимой подсистемой. Это означает, что базис такой системы совпадает с ней самой. Базис ступенчатой системы векторов тоже совпадает с ней самой, в силу ее линейной независимости.

Теорема 7.3. Два различных базиса одной и той же системы векторов содержат одинаковое количество векторов.

Доказательство. Пусть S –данная система векторов. Векторы а₁, а₂, …, а_m – базис S' системы S, векторы b₁, b₂, …, b_k – базис S'' системы S. Так как а₁, а₂, …, а_m – базис, то b₁, b₂, …, b_k  L(а₁, а₂, …, а_m) и b₁, b₂, …, b_k линейно независимы, тогда по следствию из двух терем 7.1 и 7.2 k  m.

Так как b₁, b₂, …, b_k – базис, то а₁, а₂, …, а_m  L(b₁, b₂, …, b_k) и а₁, а₂, …, а_m – линейно независимы, тогда по тому же следствию m  k, и окончательно получаем, что m = k. Теорема доказана.

Базис пространства Rn

Векторы e₁, e₂, …, e_n образуют базис пространства Rⁿ, так как e₁, e₂, …, e_n – линейно независимы, и каждый вектор из Rⁿ линейно выражается через эти векторы. По предыдущей теореме 7.3 в другом базисе Rⁿ должно быть столько же векторов, сколько и в этом, то есть n. Сформулируем этот вывод в виде теоремы.

Теорема 7.4. Базисы пространства Rⁿ – это в точности все линейно независимые системы, состоящие из n векторов.

Другими словами, система, состоящая из n линейно независимых векторов – это базис, и наоборот, базис Rⁿ – это система, состоящая из n линейно независимых векторов.

Ранг системы векторов

Дадим два равносильных определения ранга системы векторов.

Определение 7.16. Рангом системы векторов называется количество векторов в любом базисе этой системы.

Определение 7.17. Рангом системы векторов называется максимальное число линейно независимых векторов в этой системе.

Если дана система векторов а₁, а₂, …, а_m пространства Rⁿ, то ранг r этой системы не больше количества векторов в ней и не больше размерности пространства Rⁿ, то есть r  m и r  n, или r  min(m, n).

Ранг линейно независимой системы векторов равен количеству векторов в ней.

Ранг ступенчатой системы векторов равен количеству векторов в ней.

Лемма 7.1 (о ранге системы векторов). Ранг системы векторов не изменится, если к ней добавить (или удалить) вектор, являющийся линейной комбинацией остальных.

На основании этой леммы можно доказать теорему.

Теорема 7.5. Ранг системы векторов не меняется при следующих преобразованиях, называемых элементарными:

умножение вектора на число, не равное нулю;
прибавление к одному вектору другого, умноженного на произвольное число;
удаление нулевого вектора.

С помощью этих преобразований векторы системы можно поменять местами.

Практическое нахождение ранга и базиса системы векторов

Из данной системы векторов составляем матрицу, расположив векторы как строки этой матрицы. Приводим матрицу к ступенчатому виду с помощью элементарных преобразований над строками этой матрицы. При этом не меняется ни ранг матрицы, ни ранг системы векторов-строк. Ранг полученной ступенчатой матрицы, а также полученной ступенчатой системы векторов равен количеству оставшихся ненулевых строк. Базисом системы векторов являются те векторы, на месте которых остались ненулевые строки.

Пример 7.4. Найти ранг и базис системы векторов а₁ = (1, 3, 0, 5), а₂ = (1, 2, 0, 4), а₃ = (1, 1, 1, 3) а₄ = (1, 0, –1, 0), а₅ = (1, –3, 3, –1).

Решение. Действуем по описанной схеме.

    .

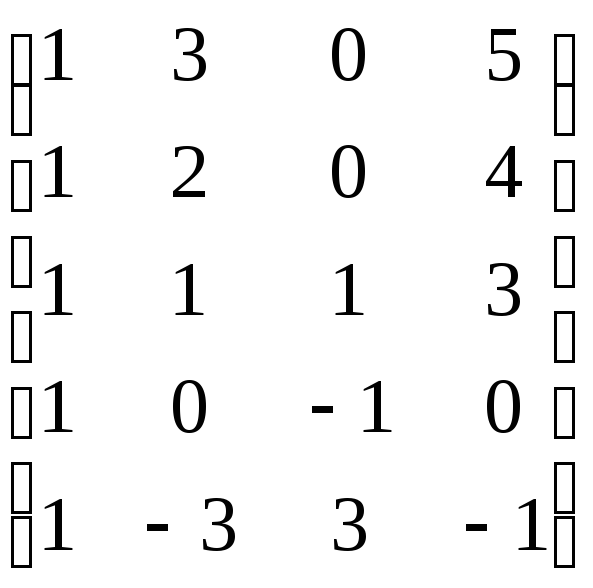
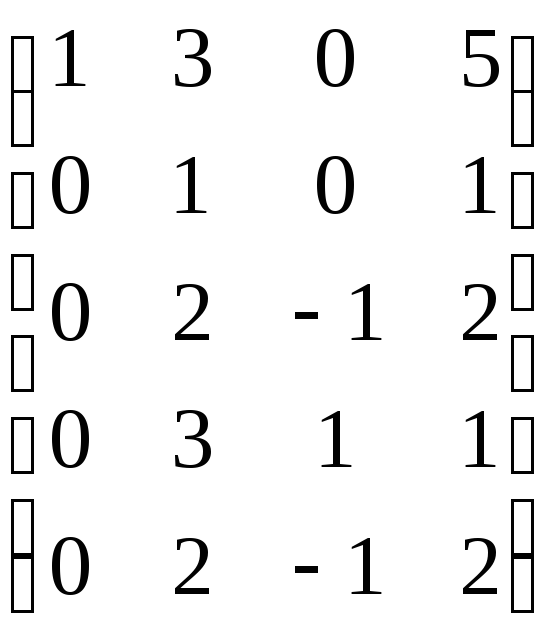
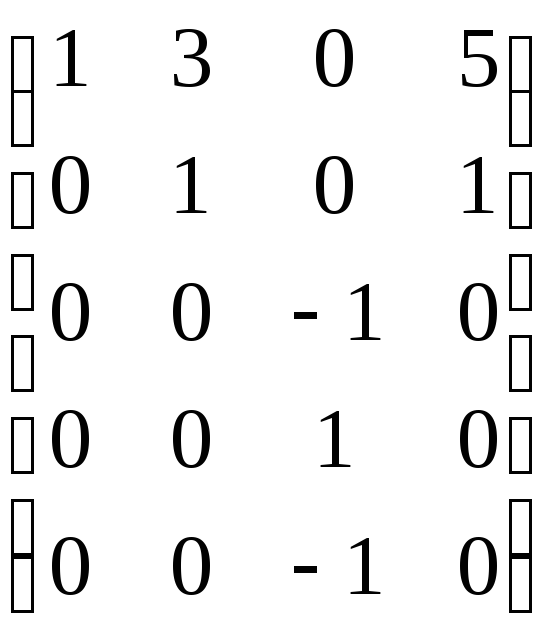
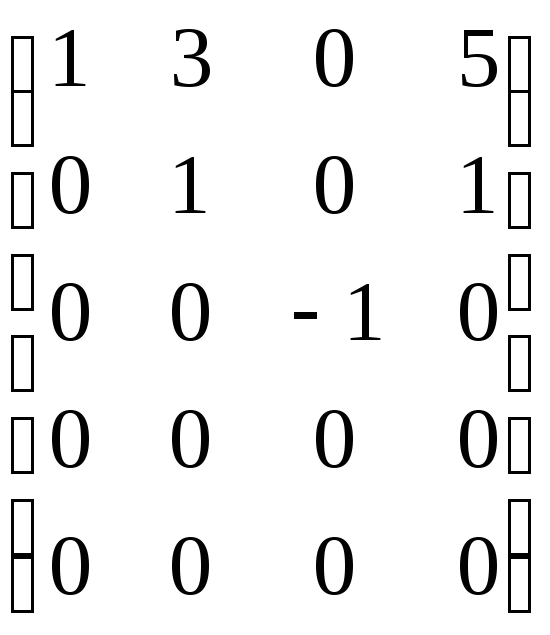
Ранг системы векторов равен трем (по количеству оставшихся ненулевых строк), один из базисов образуют векторы а₁, а₂, а₃.

Нахождение ранга системы векторов позволяет решать вопрос о линейной зависимости системы векторов. Если ранг системы векторов равен количеству векторов в системе, то эта система линейно независима, если же ранг системы векторов меньше количества векторов в системе, то эта система векторов линейно зависима.

Так как ранг рассмотренной системы (пример 7.4) векторов а₁, а₂, а₃, а₄, а₅ равен трем и меньше числа векторов, то есть пяти, то система векторов а₁, а₂, а₃, а₄, а₅ линейно зависима.

8. Векторные (линейные) пространства

8.1. Определение векторного пространства над произвольным полем.

Пусть P – произвольное поле. Известные нам примеры полей – поле рациональных, действительных, комплексных чисел.

Определение 8.1. Множество V называется векторным (или линейным) пространством над полем P, если для каждых двух элементов a, b  V определена сумма a + b  V,и для каждого k  P и для каждого a  V определено произведение ka  V, причем справедливы следующие равенства: для любых a, b, c  V и любых k, l  P

a + b = b + a;
a + (b + c) = (a + b) + c;
 о  V : a + о = a;
 а,  (–а) : a + (–a) = о;
1a = a, 1  P;
k(la) = l(ka) = (lk)a;
(k + l)a = ka + la;
k(a + b) = ka + kb.

Элементы векторного пространства принято называть векторами, о - нулевой вектор; (–а) – вектор, противоположный вектору а; 1  P – единица поля P.

Примеры 8.1. Приведем примеры векторных пространств.

1) Rⁿ – арифметическое n-мерное векторное пространство.

2) Множество матриц одного итого же размера с действительными коэффициентами R^m^ⁿ, сложение матриц и умножение их на действительное число определены.

3) R[x] – множество многочленов с действительными коэффициентами, сложение многочленов и умножение их на действительное число известны.

4) R[x]₍__n₎ – множество многочленов с действительными коэффициентами степени, не превосходящей n.

5) Множество направленных отрезков плоскости или пространства с общим началом в начале координат. Сложение таких отрезков осуществляется по правилу параллелограмма, умножение по известному правилу.

6) R(a, b) – множество функций определенных, дифференцируемых на отрезке [a, b].

Если числа в определении 8.1 k, l … брать из поля действительных (вещественных) чисел R, т. е. Р = R, то пространство называется вещественным векторным (линейным) пространством; если же из поля комплексных чисел, то приходим к понятию комплексного линейного пространства.

Простейшие свойства векторных пространств

1) о – нулевой вектор (элемент), определен единственным образом в произвольном векторном пространстве над полем.

2) Для любого вектора a  V существует единственный противоположный элемент (–a)  V.

3) a, b  V уравнение а + х = b разрешимо единственным образом x = b + (–a) и обозначается как x = b – a, и называется разностью.

4) операция сложения сократима: если а + b = a + c, то b = c для любых a, b, c  V.

5) если а + b = a, то b = o.

6) если а + b = о, то а = –b и b = –a.

7) –(–а) = а.

8) 0а = о, где 0 элемент поля P, а о – нулевой вектор пространства V.

9) kо = о, здесь k  P, о  V.

10) если kа = о, то k = 0 или а =о.

11) (–1)а = –а.

12) (k – l)a = ka – la, где k, l  P, а  V.

13) k(a – b) = ka – kb, где k  P, а, b  V.

14) (–k)а = –kа.

Линейная зависимость и независимость системы векторов

Для произвольного векторного пространства понятия линейной комбинации, линейной оболочки системы векторов, линейной зависимости и независимости системы векторов определяется точно так, как и для n-мерного арифметического векторного пространства. Выполняются все свойства линейной зависимости (кроме свойства, связанного со ступенчатой системой векторов).