ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 11.08.2024
Просмотров: 568
Скачиваний: 0
СОДЕРЖАНИЕ
Т. Н. Матыцина е. К. Коржевина линейная алгебра
1.1. Множества и их элементы. Способы задания множеств
1.2. Подмножества. Диаграммы Эйлера – Венна
1.3. Операции над множествами и их свойства
2. Пересечение (или произведение).
4. Декартовое произведение (или прямое произведение).
Свойства операций над множествами
1.4. Метод математической индукции
Операции над комплексными числами
Геометрическая интерпретация комплексных чисел
Тригонометрическая форма комплексного числа
Действия над комплексными числами в тригонометрической форме
4. Извлечение корня n-ой степени.
Показательная форма комплексного числа
Способы задания бинарных отношений
Операции над бинарными отношениями
2.2. Свойства бинарных отношений
2.3. Отношение эквивалентности
3. Матрицы и действия над ними
3.2. Основные операции над матрицами и их свойства
3.2.1. Сложение однотипных матриц
3.2.2. Умножение матрицы на число
4. Определители квадратных матриц
4.1. Определители матриц второго и третьего порядка
4.2. Определитель матрицы n-го порядка
4.4. Практическое вычисление определителей
5. Ранг матрицы. Обратная матрица
5.2. Нахождение ранга матрицы методом окаймления миноров
5.3. Нахождение ранга матрицы с помощью элементарных преобразований
5.4. Понятие обратной матрицы и способы ее нахождения
Алгоритм нахождения обратной матрицы
Нахождение обратной матрицы с помощью элементарных преобразований
6.1. Основные понятия и определения
6.2. Методы решения систем линейных уравнений
6.3. Исследование системы линейных уравнений
6.4. Однородные системы линейных уравнений
Свойства решений однородной системы линейных уравнений
Фундаментальный набор решений однородной системы линейных уравнений
7. Арифметическое n-мерное векторное пространство
7.2. Линейная зависимость и независимость системы векторов
Свойства линейной зависимости системы векторов
Две теоремы о линейной зависимости
7.3. Базис и ранг системы векторов
8. Векторные (линейные) пространства
8.1. Определение векторного пространства над произвольным полем.
Простейшие свойства векторных пространств
Линейная зависимость и независимость системы векторов
8.2. Подпространства. Линейные многообразия
Пересечение и сумма подпространств
8.3. Базис и размерность векторного пространства
8.3.1. Конечномерные векторные пространства
Базис конечномерного векторного пространства
8.3.2. Базисы и размерности подпространств
8.3.3. Координаты вектора относительно данного базиса
8.3.4. Координаты вектора в различных базисах
8.4 Евклидовы векторные пространства
Скалярное произведение в координатах
Скалярное произведение в ортонормированном базисе
Ортогональное дополнение подпространства
9.1. Основные понятия и способы задания линейных операторов
Способы задания линейных операторов
9.2. Матрица линейного оператора Связь между координатами вектора и координатами его образа
Матрицы линейного оператора в различных базисах
Свойства отношения подобия матриц
9.4. Действия над линейными операторами
1. Сложение линейных операторов.
Свойства сложения линейных операторов
9.5. Ядро и образ линейного оператора
9.6. Обратимые линейные операторы
9.7. Собственные векторы линейного оператора
9.7.1. Свойства собственных векторов
9.7.2. Характеристический многочлен матрицы
9.7.3. Нахождение собственных векторов линейного оператора
9.7.4. Алгоритм нахождения собственных векторов линейного оператора
9.7.5.Условия, при которых матрица подобна диагональной матрице
10. Жорданова нормальная форма матрицы линейного оператора
10.2. Жорданова нормальная форма
10.3.Приведение матрицы к жордановой (нормальной) форме
Алгоритм приведения матрицы a к жордановой форме
11. Билинейные и квадратичные формы
Преобразование матрицы билинейной формы при переходе к новому базису. Ранг билинейной формы
Приведение квадратичной формы к каноническому виду
Закон инерции квадратичных форм
Классификация квадратичных форм
Необходимое и достаточное условие знакоопределенности квадратичной формы
Необходимое и достаточное условие знакопеременности квадратичной формы
Необходимое и достаточное условие квазизнакопеременности квадратичной формы
7. Арифметическое n-мерное векторное пространство
7.1. Основные понятия
В предыдущих разделах уже встречалось понятие о наборе из действительных чисел, расположенных в определенном порядке. Это матрица-строка (или матрица-столбец) и решение системы линейных уравнений с n неизвестными. Эти сведения можно обобщить.
Определение 7.1. n-мерным арифметическим вектором называется упорядоченный набор из n действительных чисел.
Значит а = (1, 2, …, n), где i R, i = 1, 2, …, n – общий вид вектора. Число n называется размерностью вектора, а числа i называются его координатами.
Например:
а = (1,
–8, 7, 4,
![]() )
– пятимерный вектор.
)
– пятимерный вектор.
Все множество n-мерных векторов принято обозначать как Rn.
Определение 7.2. Два вектора а = (1, 2, …, n) и b = (1, 2, …, n) одинаковой размерности равны тогда и только тогда, когда равны их соответствующие координаты, т. е. 1 = 1, 2 = 2, …, n = n.
Определение 7.3. Суммой двух n-мерных векторов а = (1, 2, …, n) и b = (1, 2, …, n) называется вектор a + b = (1 + 1, 2 + 2, …, n + n).
Определение 7.4. Произведением действительного числа k на вектор а = (1, 2, …, n) называется вектор kа = (k1, k2, …, kn)
Определение 7.5. Вектор о = (0, 0, …, 0) называется нулевым (или нуль–вектором).
Легко проверить, что действия (операции) сложения векторов и умножения их на действительное число обладают следующими свойствами: a, b, c Rn, k, l R :
a + b = b + a;
a + (b + c) = (a + b) + c;
a + о = a;
a + (–a) = о;
1a = a, 1 R;
k(la) = l(ka) = (lk)a;
(k + l)a = ka + la;
k(a + b) = ka + kb.
Определение 7.6. Множество Rn с заданными на нем операциями сложения векторов и умножения их на действительное число называется арифметическим n-мерным векторным пространством.
7.2. Линейная зависимость и независимость системы векторов
Пусть а1, а2, …, аm множество из m штук n-мерных векторов, о котором принято говорить – система векторов, и k1, k2, …, km – произвольные действительные числа.
Определение 7.7. Линейной комбинацией системы векторов а1, а2, …, аm с коэффициентами k1, k2, …, km называется вектор b = k1а1 + k2а2 + … + kmаm.
Принято говорить: вектор b линейно выражается через векторы а1, а2, …, аm или вектор b разложен (раскладывается) по векторам а1, а2, …, аm.
Пример 7.1. Даны векторы а1 = (3, 2, –1, 0), а2 = (–1, 0, 4, 1), а3 = (–2, –2, –3, –1). Найти вектор b = 2а1 – а2 – а3.
Решение. b = 2а1 – а2 – а3 = 2(3, 2, –1, 0) + (–1)(–1, 0, 4, 1) + (–1)(–2, –2, –3, –1) = (6, 4, –2, 0) + (1, 0, –4, –1) + (2, 2, 3, 1) = (9, 6, –3, 0).
Пример 7.2. Даны векторы а1 = (6, 4, –2), а2 = (–1, 0, 4), а3 = (–2, –2, –3). Найти вектор b = а1 + 2а2 + 2а3.
Решение. b = а1 + 2а2 + 2а3 = (6, 4, –2) + 2(–1, 0, 4) + 2(–2, –2, –3) = = (6, 4, –2) + (–2, 0, 8) + (–4, –4, –6) = (0, 0, 0) = о.
Определение 7.8. Линейной оболочкой системы векторов а1, а2, …, аm называется множество всех линейных комбинаций этих векторов. Принятое обозначение: L(а1, а2, …, аm).
Из определения следует, что
L(а1, а2, …, аm) = {k1а1 + k2а2 + … + kmam, ki R}.
Если вектор b линейно выражается через векторы а1, а2, …, аm, то в этих обозначениях можно записать, что b L(а1, а2, …, аm).
Определение 7.9. Линейная комбинация системы векторов а1, а2, …, аm вида 0а1 + 0а2 + … + 0аm называется нулевой. Нулевая линейная комбинация векторов равна нулевому вектору.
Определение 7.10. Система векторов а1, а2, …, аm называется линейно независимой, если линейная комбинация этих векторов равна нулевому вектору тогда и только тогда, когда эта комбинация нулевая, то есть
k1а1 + k2а2 + … + kmam = о k1 = 0, k2 = 0, …, km = 0.
Равносильное определение линейно независимой системы векторов звучит следующим образом: система векторов линейно независима тогда и только тогда, когда ни один вектор нельзя выразить через остальные векторы.
Определение 7.11. Система векторов а1, а2, …, аm называется линейно зависимой, если существуют коэффициенты k1, k2,…, km, не все одновременно равные нулю и такие, что k1а1 + k2а2 + … + kmam = о.
Равносильное определение линейно зависимой системы векторов звучит следующим образом: система векторов линейно зависима тогда и только тогда, когда в этой системе существует хотя бы один вектор, который линейно выражается через остальные.
Если система векторов состоит только из одного вектора, то эта система линейно зависима, если этот вектор нулевой, и линейно независима, если он ненулевой.
Система векторов, содержащая два вектора, линейно зависима в случае пропорциональности координат этих векторов, и линейно независима в противном случае.
Свойства линейной зависимости системы векторов
1) Система векторов, содержащая нулевой вектор, линейно зависима.
2) Система векторов линейно зависима, если какая-нибудь ее подсистема линейно зависима.
Следствие. Если система векторов линейно независима, то и любая ее подсистема линейно независима.
3) Если к линейно независимой системе векторов а1, а2, …, аm добавить вектор b и при этом система векторов а1, а2, …, аm, b станет линейно зависимой, то вектор b линейно выражается через остальные.
Определение7.12. Система векторов а1, а2, …, аm называется ступенчатой (или лестничной), если матрица, составленная из координат этих векторов, является ступенчатой, т. е.
а1 = (а11, а12, …, а1r, …, а1n), а11 ≠ 0;
а2 = (0, а22, …, а2r, …, а2n), а22 ≠ 0;
……………………………………
аm = (0, 0, …, аrr, …, аrn), аrr ≠ 0.
4) Ступенчатая система векторов линейно независима.
Пример 7.3. Выяснить является ли система векторов а1 = (2, 2, 7, –1), а2 = (3, –1, 2, 4), а3 = (1, 1, 3, 1) линейно зависимой.
Решение. По определениям 7.10 и 7.11 составим линейную комбинацию данных векторов k1а1 + k2а2 + k3а3 = 0; подставим вместо векторов их координаты:
k1(2, 2, 7, –1) + k2(3, –1, 2, 4) + k3(1, 1, 3, 1) = (0, 0, 0, 0).
Данное векторное равенство (согласно определению 7.2 о равенстве векторов) запишем для каждой координаты, и получим систему:
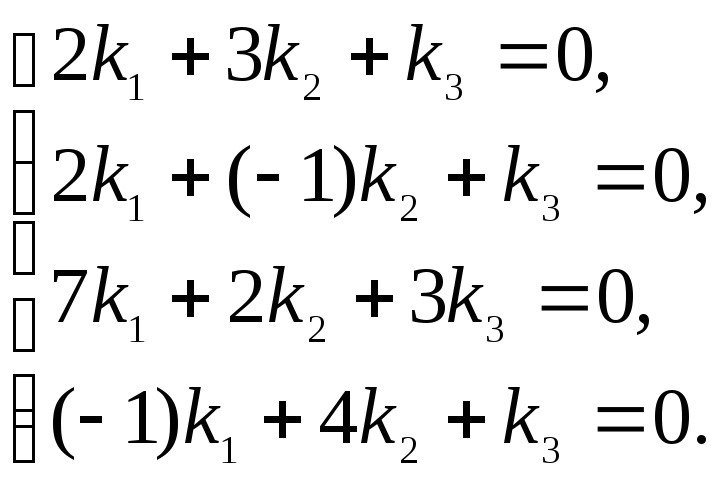
Решим систему методом Гаусса.
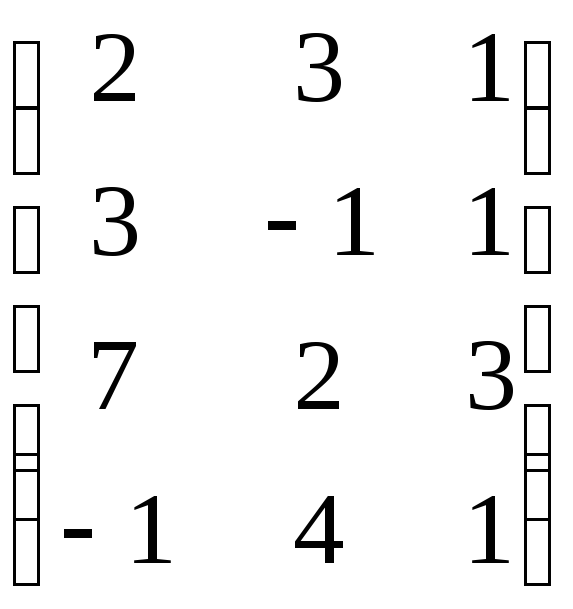
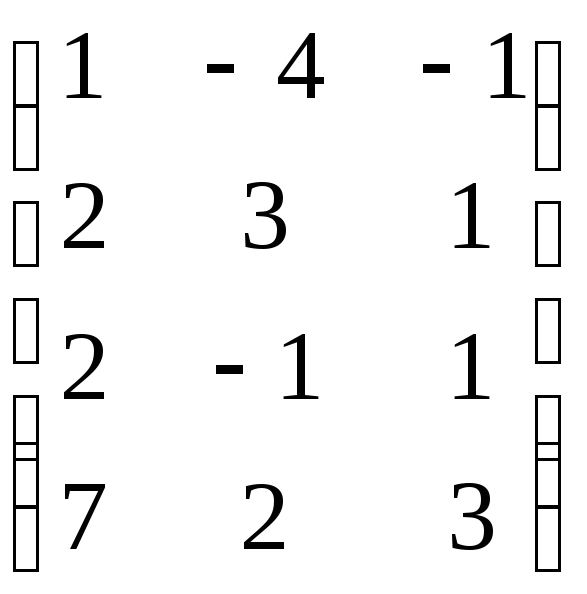
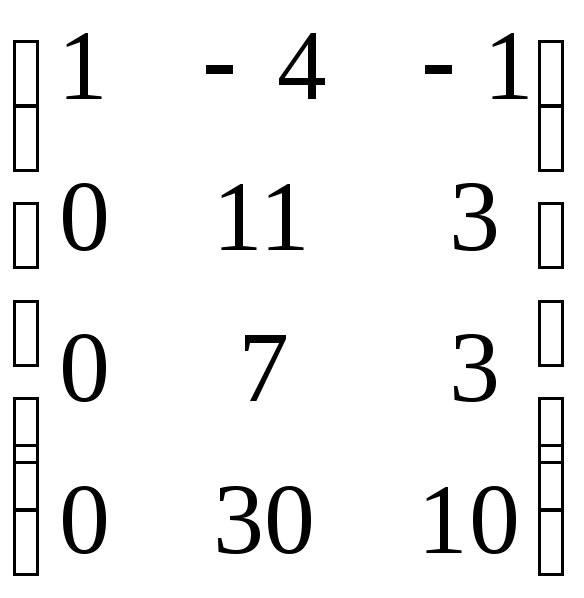
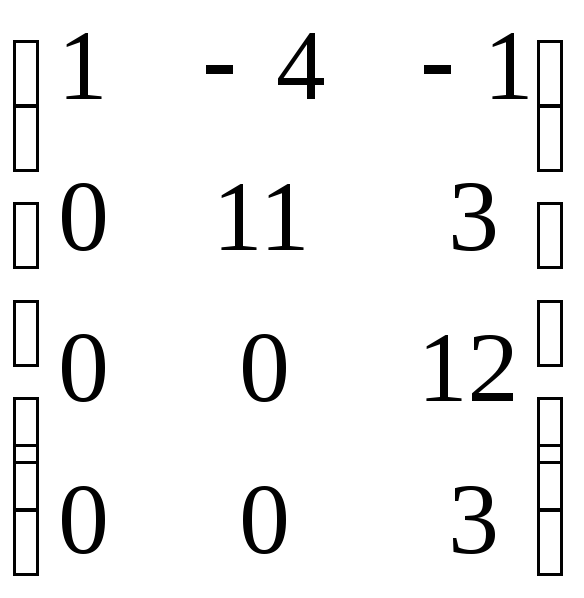
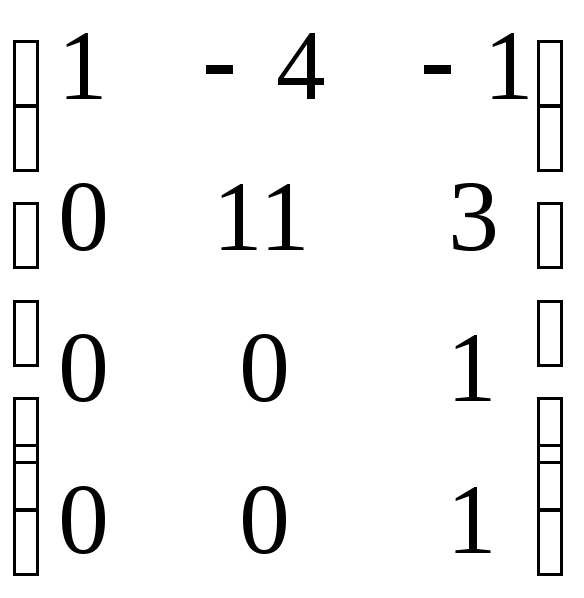
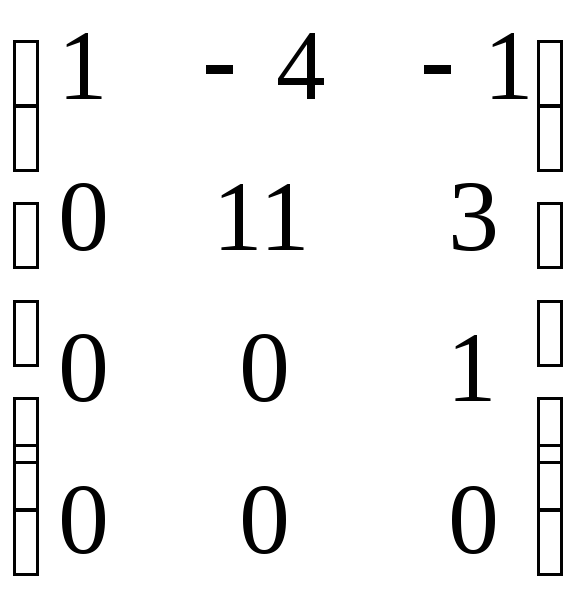

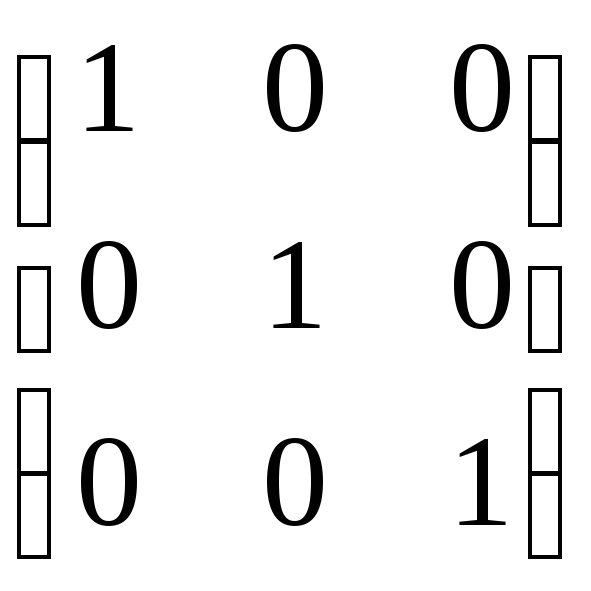
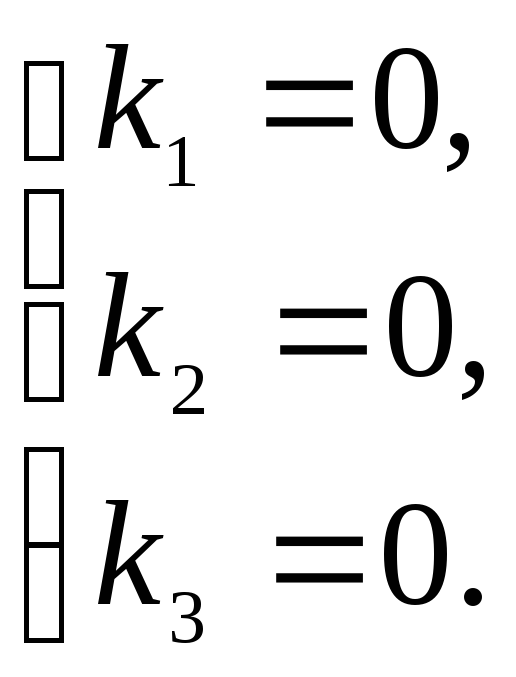
Следовательно, данная система векторов линейно независима.
Единичная система векторов
Определение 7.13. Системой единичных векторов пространства Rn называется система векторов e1, e2, …, en, где e1 = (1, 0, …, 0), e2 = (0, 1, …, 0), …, en = (0, 0, …, 1).
Выпишем единичные векторы для пространств R3 и R4:
e1 = (1, 0, 0), e2 = (0, 1, 0), e3 = (0, 0, 1);
e1 = (1, 0, 0, 0), e2 = (0, 1, 0, 0), e3 = (0, 0, 1, 0), e4 = (0, 0, 0, 1).
Из свойств линейной зависимости следует, что единичная система векторов линейно независима. Любой вектор а = (1, 2, …, n) пространства Rn может быть представлен в виде линейной комбинации единичных векторов. Например, если а = (–2, 4, 7), то а = (–2)e1 + 4e2 + 7e3.
Вывод. В пространстве Rn существует n линейно независимых векторов, через которые линейно выражаются все векторы пространства Rn.
Две теоремы о линейной зависимости
Теорема 7.1. Если большая система векторов линейно выражается через меньшую, то большая система линейно зависима.
Сформулируем эту теорему подробнее: пусть а1, а2, …, аm и b1, b2, …, bk две системы векторов и m > k, то есть первая система большая. Если а1, а2, …, аm L(b1, b2, …, bk), то система векторов а1, а2, …, аm линейно зависима.
Теорема 7.2. В пространстве Rn любая система, состоящая более чем из n векторов, линейно зависима.
Это следует из того, что в Rn любая система выражается через систему e1, e2, …, en.
Следствие. Если а1, а2, …, аm L(b1, b2, …, bk) и система а1, а2, …, аm линейно независима, то m k.
7.3. Базис и ранг системы векторов
Пусть S – система векторов пространства Rn; она может быть как конечной, так и бесконечной. S' – подсистема системы S, S' S. Дадим два равносильных определения.