ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 11.08.2024
Просмотров: 602
Скачиваний: 0
СОДЕРЖАНИЕ
Т. Н. Матыцина е. К. Коржевина линейная алгебра
1.1. Множества и их элементы. Способы задания множеств
1.2. Подмножества. Диаграммы Эйлера – Венна
1.3. Операции над множествами и их свойства
2. Пересечение (или произведение).
4. Декартовое произведение (или прямое произведение).
Свойства операций над множествами
1.4. Метод математической индукции
Операции над комплексными числами
Геометрическая интерпретация комплексных чисел
Тригонометрическая форма комплексного числа
Действия над комплексными числами в тригонометрической форме
4. Извлечение корня n-ой степени.
Показательная форма комплексного числа
Способы задания бинарных отношений
Операции над бинарными отношениями
2.2. Свойства бинарных отношений
2.3. Отношение эквивалентности
3. Матрицы и действия над ними
3.2. Основные операции над матрицами и их свойства
3.2.1. Сложение однотипных матриц
3.2.2. Умножение матрицы на число
4. Определители квадратных матриц
4.1. Определители матриц второго и третьего порядка
4.2. Определитель матрицы n-го порядка
4.4. Практическое вычисление определителей
5. Ранг матрицы. Обратная матрица
5.2. Нахождение ранга матрицы методом окаймления миноров
5.3. Нахождение ранга матрицы с помощью элементарных преобразований
5.4. Понятие обратной матрицы и способы ее нахождения
Алгоритм нахождения обратной матрицы
Нахождение обратной матрицы с помощью элементарных преобразований
6.1. Основные понятия и определения
6.2. Методы решения систем линейных уравнений
6.3. Исследование системы линейных уравнений
6.4. Однородные системы линейных уравнений
Свойства решений однородной системы линейных уравнений
Фундаментальный набор решений однородной системы линейных уравнений
7. Арифметическое n-мерное векторное пространство
7.2. Линейная зависимость и независимость системы векторов
Свойства линейной зависимости системы векторов
Две теоремы о линейной зависимости
7.3. Базис и ранг системы векторов
8. Векторные (линейные) пространства
8.1. Определение векторного пространства над произвольным полем.
Простейшие свойства векторных пространств
Линейная зависимость и независимость системы векторов
8.2. Подпространства. Линейные многообразия
Пересечение и сумма подпространств
8.3. Базис и размерность векторного пространства
8.3.1. Конечномерные векторные пространства
Базис конечномерного векторного пространства
8.3.2. Базисы и размерности подпространств
8.3.3. Координаты вектора относительно данного базиса
8.3.4. Координаты вектора в различных базисах
8.4 Евклидовы векторные пространства
Скалярное произведение в координатах
Скалярное произведение в ортонормированном базисе
Ортогональное дополнение подпространства
9.1. Основные понятия и способы задания линейных операторов
Способы задания линейных операторов
9.2. Матрица линейного оператора Связь между координатами вектора и координатами его образа
Матрицы линейного оператора в различных базисах
Свойства отношения подобия матриц
9.4. Действия над линейными операторами
1. Сложение линейных операторов.
Свойства сложения линейных операторов
9.5. Ядро и образ линейного оператора
9.6. Обратимые линейные операторы
9.7. Собственные векторы линейного оператора
9.7.1. Свойства собственных векторов
9.7.2. Характеристический многочлен матрицы
9.7.3. Нахождение собственных векторов линейного оператора
9.7.4. Алгоритм нахождения собственных векторов линейного оператора
9.7.5.Условия, при которых матрица подобна диагональной матрице
10. Жорданова нормальная форма матрицы линейного оператора
10.2. Жорданова нормальная форма
10.3.Приведение матрицы к жордановой (нормальной) форме
Алгоритм приведения матрицы a к жордановой форме
11. Билинейные и квадратичные формы
Преобразование матрицы билинейной формы при переходе к новому базису. Ранг билинейной формы
Приведение квадратичной формы к каноническому виду
Закон инерции квадратичных форм
Классификация квадратичных форм
Необходимое и достаточное условие знакоопределенности квадратичной формы
Необходимое и достаточное условие знакопеременности квадратичной формы
Необходимое и достаточное условие квазизнакопеременности квадратичной формы
6.2. Методы решения систем линейных уравнений
6.2.1. Метод Крамера
Рассмотрим систему линейных уравнений, в которой число уравнений равно числу неизвестных, то есть m = n и система имеет вид:
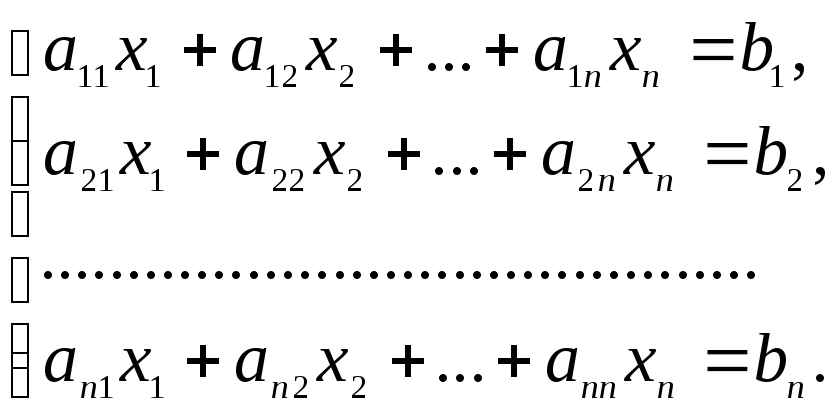
В этом случае основная матрица системы – квадратная матрица порядка n.
Теорема 6.1 (Крамера11). Пусть в системе линейных уравнений число уравнений равно числу неизвестных и определитель основной матрицы не равен нулю. Тогда решение этой системы находят по формулам:
x1 = ![]() ,
x2 =
,
x2 = ![]() ,
…, xn =
,
…, xn = ![]() ,
(3)
,
(3)
где матрица Ai получена из матрицы A заменой i-ого столбца столбцом свободных членов.
Формулы (3) называются формулами Крамера.
Пример 6.1.
Решить систему линейных уравнений по
формулам Крамера. Дана система
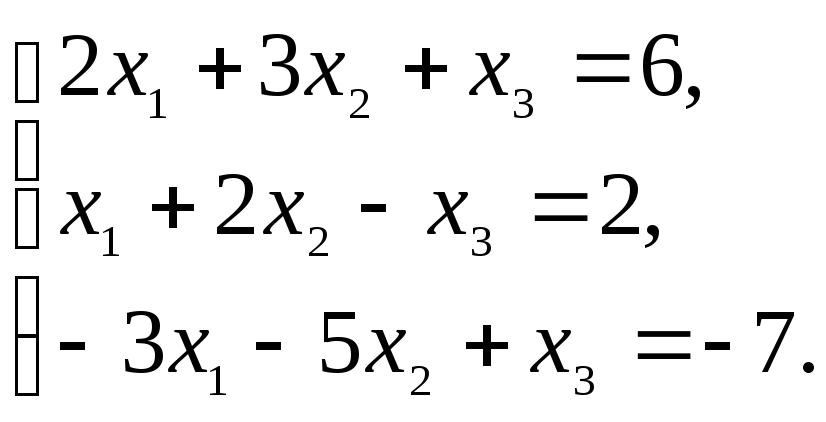
Решение.
Данной системе соответствует основная
матрица А = 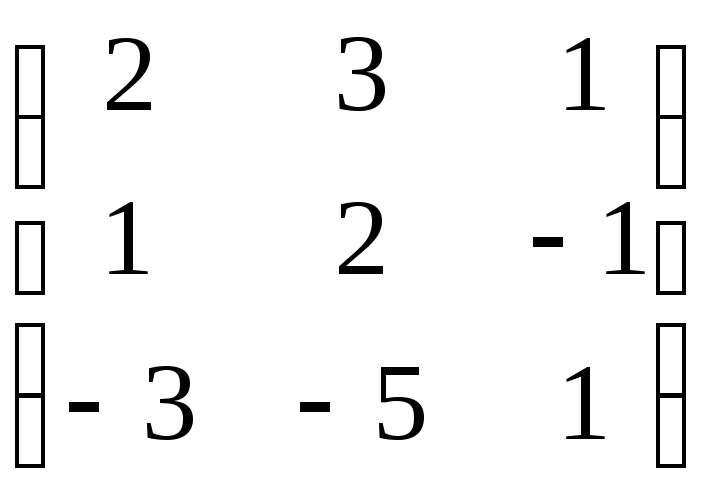 ,
столбец
свободных членов В =
,
столбец
свободных членов В = ![]() и столбец
неизвестных Х =
и столбец
неизвестных Х = ![]() .
Проверим, можно ли решать данную систему
по формулам Крамера. В
этой системе число уравнений равно
числу неизвестных. Найдем определитель
основной матрицы этой системы: |А| =
.
Проверим, можно ли решать данную систему
по формулам Крамера. В
этой системе число уравнений равно
числу неизвестных. Найдем определитель
основной матрицы этой системы: |А| = 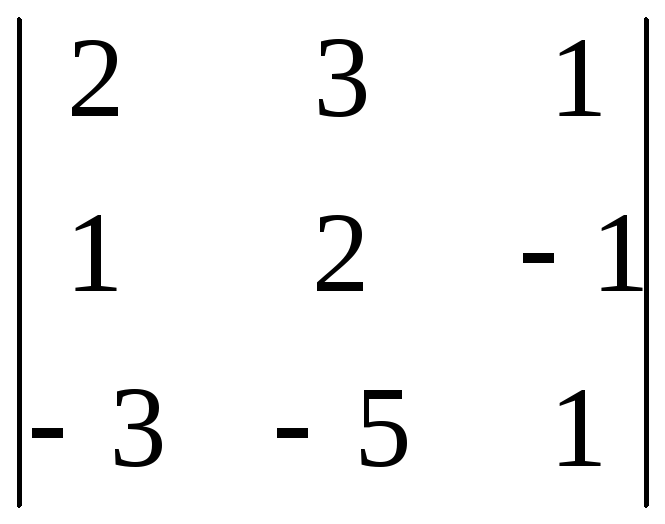 = 1.
Этот определитель не равен нулю, поэтому
систему можно решать по формулам Крамера.
Вычислим определители матриц A1,
A2,
A3:
= 1.
Этот определитель не равен нулю, поэтому
систему можно решать по формулам Крамера.
Вычислим определители матриц A1,
A2,
A3:
|A1| = 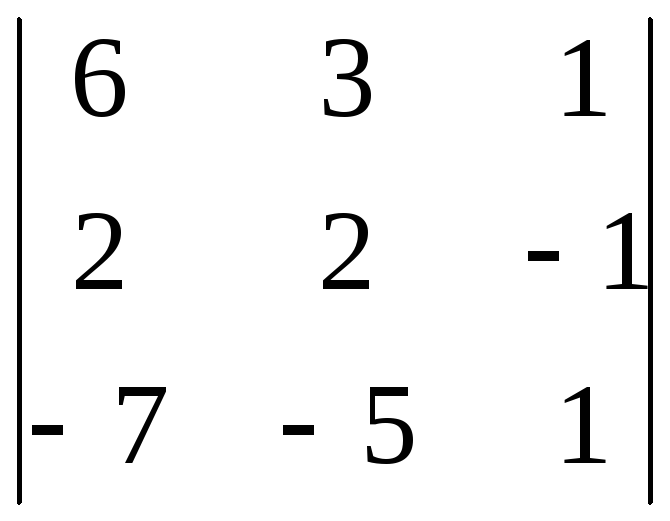 = 1,
|A2| =
= 1,
|A2| = 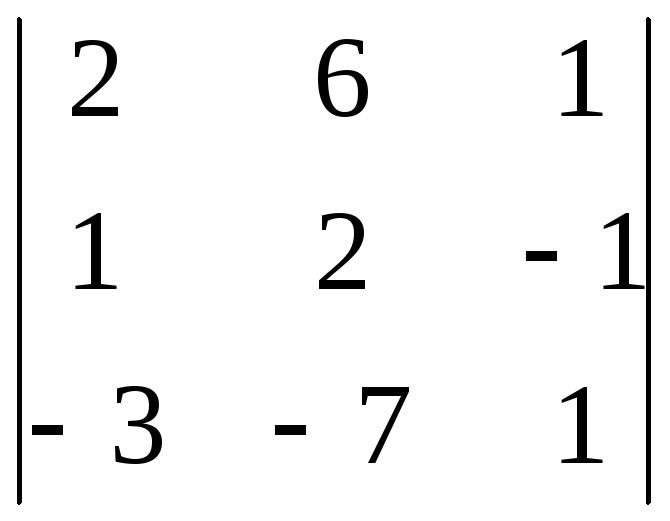 = 1,
|A3| =
= 1,
|A3| =  = 1.
= 1.
По формулам (3) находим неизвестные:
x1 = ![]() =
= ![]() = 1,
x2 =
= 1,
x2 = ![]() =
= ![]() = 1,
x3 =
= 1,
x3 = ![]() =
= ![]() = 1.
= 1.
Ответ: (1; 1, 1).
6.2.2. Метод обратной матрицы
Метод обратной матрицы применим для систем линейных уравнений, в которых число уравнений равно числу неизвестных и определитель основной матрицы не равен нулю.
Матричная форма записи системы линейных уравнений представляется в виде следующего матричного равенства: АХ = В.
В силу условия матрица А – квадратная матрица порядка n с определителем не равным нулю. Это означает, что для матрицы А существует обратная матрица А–1. Умножим обе части матричного равенства на матрицу А–1 слева. Получим А–1(АХ) = А–1В. Преобразуем данной выражение:
(А–1А)Х = А–1В;
EХ = А–1В;
Х = А–1В.
Вывод: если для системы n линейных уравнений с n неизвестными определитель основной матрицы не равен нулю, то система имеет единственное решение, которое находится по формуле Х = А–1В, где А – основная матрица данной системы, В – столбец свободных членов.
Пример 6.2.
Решить систему линейных уравнений
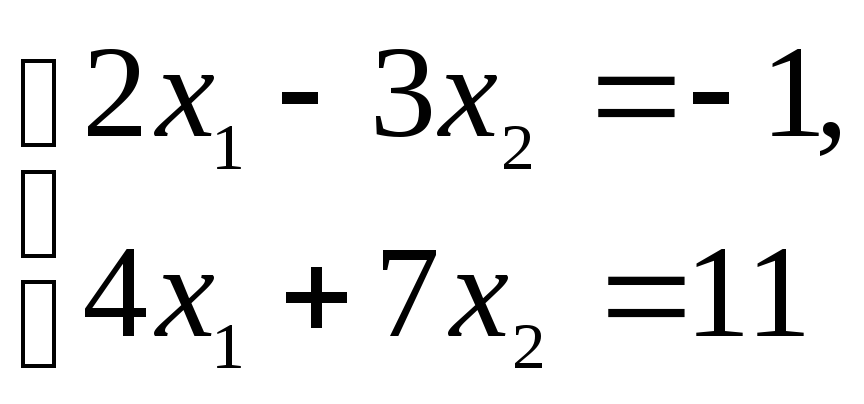 методом обратной матрицы.
методом обратной матрицы.
Решение.
Здесь А = ![]() ,
Х =
,
Х = ![]() ,
B =
,
B = ![]() .
Найдем матрицу
А–1
любым способом. Имеем А–1 =
.
Найдем матрицу
А–1
любым способом. Имеем А–1 = ![]() .
Теперь можно вычислить столбец неизвестных
X.
.
Теперь можно вычислить столбец неизвестных
X.
X = ![]() =
= ![]()
![]() =
= ![]() =
= ![]() .
Значит
x1 = 1,
x2 = 1.
.
Значит
x1 = 1,
x2 = 1.
Ответ: (1; 1).
Очевидно, что применение этих методов связано с выполнением определенных условий и решить с их помощью произвольную систему невозможно.
6.2.3. Метод Гаусса
Для описания этого метода, который годится для решения произвольных систем линейных уравнений, необходимы некоторые новые понятия.
Определение 6.7. Уравнение вида 0x1 + 0x2 + ... + 0xn = 0 называется нулевым.
Решением такого уравнения является любой вектор.
Определение 6.8. Уравнение вида 0x1 + 0x2 + ... + 0xn = b , где b ≠ 0, называется несовместным (или противоречивым).
У несовместного уравнения решений нет.
Определение 6.9. Элементарными преобразованиями системы линейных уравнений называются следующие ее преобразования:
умножение любого уравнения на число, не равное нулю;
прибавление к одному уравнению системы любого другого, умноженного на произвольное число;
вычеркивание нулевого уравнения.
Замечание 6.1. С помощью преобразований 1 и 2 уравнения системы можно поменять местами.
Теорема 6.2. Цепочка элементарных преобразований переводит исходную систему линейных уравнений в равносильную ей систему.
Описание метода Гаусса
Метод Гаусса – метод последовательного исключения неизвестных – заключается в том, что с помощью элементарных преобразований исходная система приводится к равносильной ей системе ступенчатого или треугольного вида, из которой последовательно, начиная с последних (по номеру), неизвестных находятся все остальные неизвестные. Дана система (1)
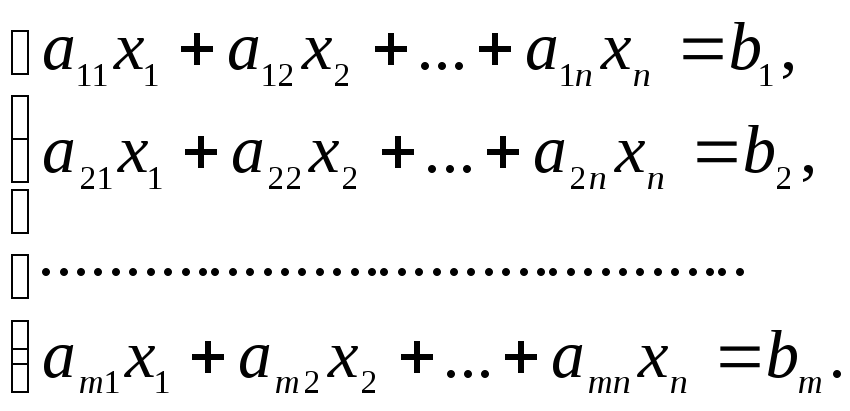 (1)
(1)
Начинаем осуществлять прямой ход. Считаем, что коэффициент а11 ≠ 0; если же это не так, меняем местами уравнения.
Первый
шаг состоит в том, чтобы исключить
неизвестное х1
из всех уравнений, кроме первого. Для
этого ко второму уравнению прибавим
первое уравнение, умноженное на число
![]() ,
к третьему уравнению прибавим первое
уравнение, умноженное на число
,
к третьему уравнению прибавим первое
уравнение, умноженное на число
![]() ,
и так далее до последнего уравнения.
После первого шага получим систему:
,
и так далее до последнего уравнения.
После первого шага получим систему:
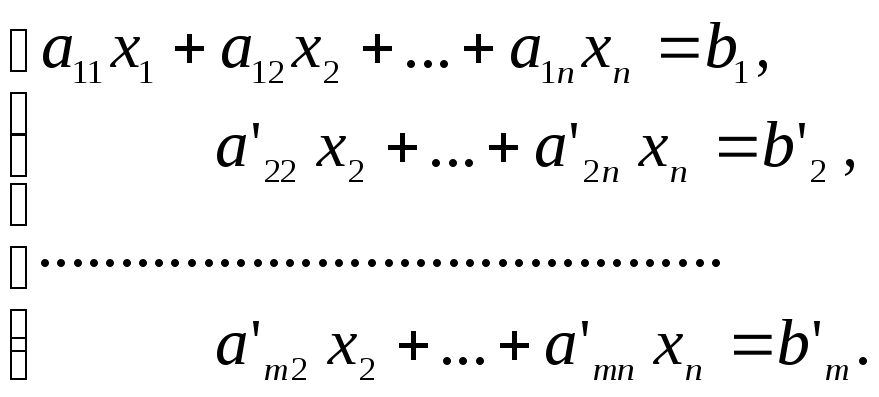
Полученная система равносильна исходной системе.
Вторым
шагом исключают неизвестное из всех
уравнений, кроме первого и второго. Для
этого повторяем все действия первого
шага для второго и последующих уравнений,
а именно: считаем, что коэффициент
![]() ≠ 0
и так далее. Если в результате преобразований
получается нулевое уравнение, то его
удаляют, если же получается несовместное
уравнение, то решение системы закончено
– она несовместна. Процесс исключения
неизвестных продолжаем до тех пор, пока
это возможно. Обозначим количество
уравнений, оставшихся после прямого
хода, через r.
Это число равно рангу основной матрицы
системы и может быть меньше или равно
n.
Рассмотрим оба случая.
≠ 0
и так далее. Если в результате преобразований
получается нулевое уравнение, то его
удаляют, если же получается несовместное
уравнение, то решение системы закончено
– она несовместна. Процесс исключения
неизвестных продолжаем до тех пор, пока
это возможно. Обозначим количество
уравнений, оставшихся после прямого
хода, через r.
Это число равно рангу основной матрицы
системы и может быть меньше или равно
n.
Рассмотрим оба случая.
1) Если r = n, то система после прямого хода принимает вид:
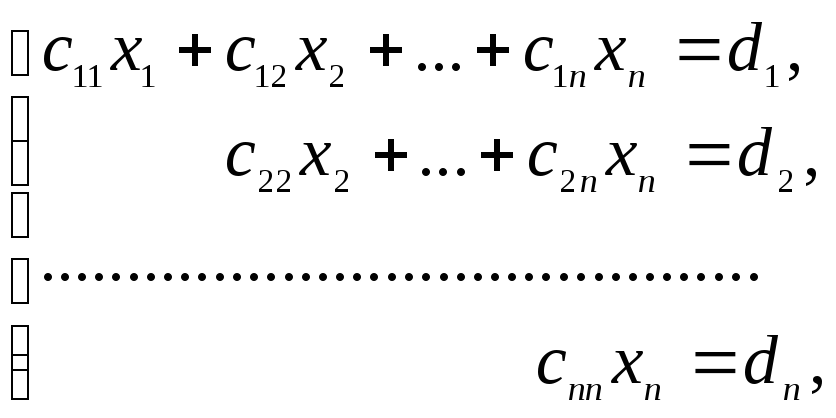
где с11 ≠ 0, с22 ≠ 0, …, сnn ≠ 0.
Обратным
ходом,
начиная с последнего уравнения,
последовательно найдем значения xn,
(где xn = ![]() ),
xn – 1,
..., x1.
В этом случае система линейных уравнений
имеет единственное решение, то есть
является определенной.
),
xn – 1,
..., x1.
В этом случае система линейных уравнений
имеет единственное решение, то есть
является определенной.
2) Если r < n, то система после прямого хода принимает вид:
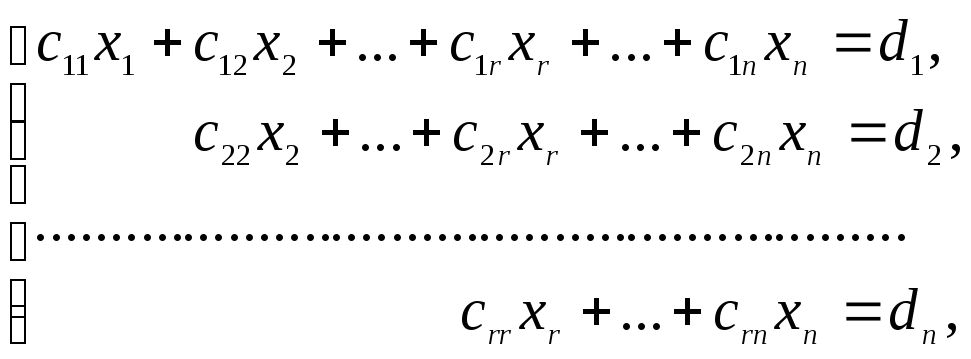
где с11 ≠ 0, с22 ≠ 0, …, сrr ≠ 0. Неизвестные x1, x2, …, xr, с которых начинаются уравнения, называются главными неизвестными, а остальные xr + 1, x r + 2, …, xn – свободными. В этом случае обратным ходом, начиная с последнего уравнения, выражают главные неизвестные через свободные неизвестные. Получают следующие равенства:
x1 = k1,r + 1xr + 1 + … + k1,nxn + t1,
x2 = k2,r + 1xr + 1 + … + k2,nxn + t2,
……………………………………..
xr = kr,r + 1xr + 1 + … + kr,nxn + tr.
Определение 6.10. Общим решением системы называется выражение главных неизвестных через свободные.
Если свободным неизвестным придать какие-нибудь числовые значения, то из общего решения получим значения главных неизвестных. Таким образом, получают частное решение системы. Из способа его получения следует, что система имеет более одного решения, то есть является неопределенной.
Пример 6.3. Решить методом Гаусса систему линейных уравнений:
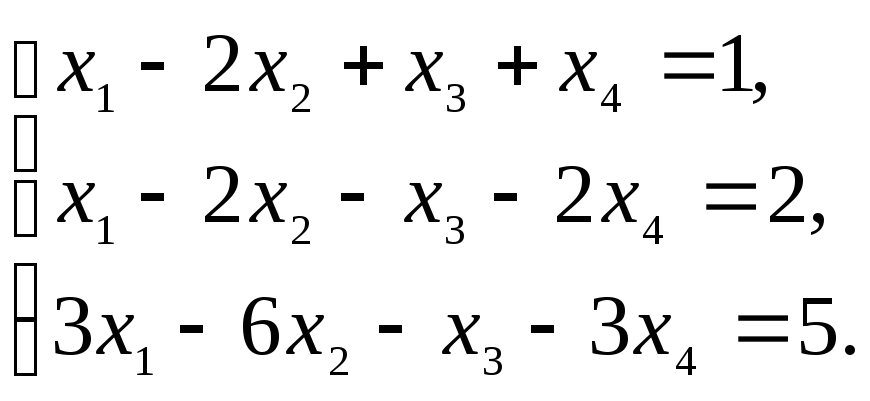
Решение.
Преобразования
с системой линейных удобнее производить
не с самими уравнениями, а с матрицей
их коэффициентов. Расширенная матрица
этой системы имеет вид: (А|B) = 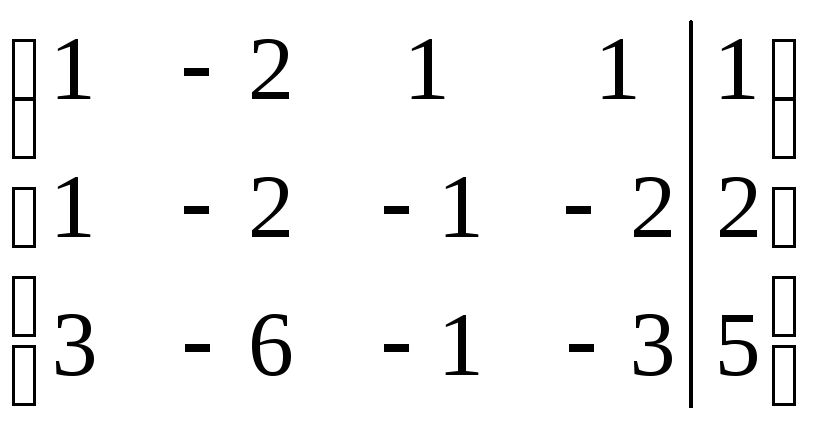 .
.
Осуществляем
прямой ход. Первым шагом исключаем
неизвестное х1
из всех уравнений, кроме первого. Так
как а11 = 1 ≠ 0,
то переставлять уравнения местами не
нужно. Прибавим ко второму уравнению
системы первое уравнение, умноженное
на (–1), к третьему уравнению – первое,
умноженное на (–3). Получим после
преобразований следующую матрицу:
 ,
в которой элемент а22 = 1.
Перестановка местами уравнений (первое
уравнение трогать не следует) не поможет,
поэтому переходим к следующему
неизвестному х3
и исключаем его из всех уравнений, кроме
первого и второго. Для этого к третьему
уравнению прибавим второе, умноженное
на (–2) и вычеркнем получившееся нулевое
уравнение. После прямого хода получаем
следующую систему:
,
в которой элемент а22 = 1.
Перестановка местами уравнений (первое
уравнение трогать не следует) не поможет,
поэтому переходим к следующему
неизвестному х3
и исключаем его из всех уравнений, кроме
первого и второго. Для этого к третьему
уравнению прибавим второе, умноженное
на (–2) и вычеркнем получившееся нулевое
уравнение. После прямого хода получаем
следующую систему:
![]() .
Прямой ход завершен. В этом случае n = 4,
r = 2,
r < n,
и, следовательно, система неопределенная.
Главные неизвестные – это те неизвестные,
с которых начинаются уравнения, в нашем
случае это х1
и х3.
Неизвестные х2
и х4
– свободные.
.
Прямой ход завершен. В этом случае n = 4,
r = 2,
r < n,
и, следовательно, система неопределенная.
Главные неизвестные – это те неизвестные,
с которых начинаются уравнения, в нашем
случае это х1
и х3.
Неизвестные х2
и х4
– свободные.