ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 11.08.2024
Просмотров: 571
Скачиваний: 0
СОДЕРЖАНИЕ
Т. Н. Матыцина е. К. Коржевина линейная алгебра
1.1. Множества и их элементы. Способы задания множеств
1.2. Подмножества. Диаграммы Эйлера – Венна
1.3. Операции над множествами и их свойства
2. Пересечение (или произведение).
4. Декартовое произведение (или прямое произведение).
Свойства операций над множествами
1.4. Метод математической индукции
Операции над комплексными числами
Геометрическая интерпретация комплексных чисел
Тригонометрическая форма комплексного числа
Действия над комплексными числами в тригонометрической форме
4. Извлечение корня n-ой степени.
Показательная форма комплексного числа
Способы задания бинарных отношений
Операции над бинарными отношениями
2.2. Свойства бинарных отношений
2.3. Отношение эквивалентности
3. Матрицы и действия над ними
3.2. Основные операции над матрицами и их свойства
3.2.1. Сложение однотипных матриц
3.2.2. Умножение матрицы на число
4. Определители квадратных матриц
4.1. Определители матриц второго и третьего порядка
4.2. Определитель матрицы n-го порядка
4.4. Практическое вычисление определителей
5. Ранг матрицы. Обратная матрица
5.2. Нахождение ранга матрицы методом окаймления миноров
5.3. Нахождение ранга матрицы с помощью элементарных преобразований
5.4. Понятие обратной матрицы и способы ее нахождения
Алгоритм нахождения обратной матрицы
Нахождение обратной матрицы с помощью элементарных преобразований
6.1. Основные понятия и определения
6.2. Методы решения систем линейных уравнений
6.3. Исследование системы линейных уравнений
6.4. Однородные системы линейных уравнений
Свойства решений однородной системы линейных уравнений
Фундаментальный набор решений однородной системы линейных уравнений
7. Арифметическое n-мерное векторное пространство
7.2. Линейная зависимость и независимость системы векторов
Свойства линейной зависимости системы векторов
Две теоремы о линейной зависимости
7.3. Базис и ранг системы векторов
8. Векторные (линейные) пространства
8.1. Определение векторного пространства над произвольным полем.
Простейшие свойства векторных пространств
Линейная зависимость и независимость системы векторов
8.2. Подпространства. Линейные многообразия
Пересечение и сумма подпространств
8.3. Базис и размерность векторного пространства
8.3.1. Конечномерные векторные пространства
Базис конечномерного векторного пространства
8.3.2. Базисы и размерности подпространств
8.3.3. Координаты вектора относительно данного базиса
8.3.4. Координаты вектора в различных базисах
8.4 Евклидовы векторные пространства
Скалярное произведение в координатах
Скалярное произведение в ортонормированном базисе
Ортогональное дополнение подпространства
9.1. Основные понятия и способы задания линейных операторов
Способы задания линейных операторов
9.2. Матрица линейного оператора Связь между координатами вектора и координатами его образа
Матрицы линейного оператора в различных базисах
Свойства отношения подобия матриц
9.4. Действия над линейными операторами
1. Сложение линейных операторов.
Свойства сложения линейных операторов
9.5. Ядро и образ линейного оператора
9.6. Обратимые линейные операторы
9.7. Собственные векторы линейного оператора
9.7.1. Свойства собственных векторов
9.7.2. Характеристический многочлен матрицы
9.7.3. Нахождение собственных векторов линейного оператора
9.7.4. Алгоритм нахождения собственных векторов линейного оператора
9.7.5.Условия, при которых матрица подобна диагональной матрице
10. Жорданова нормальная форма матрицы линейного оператора
10.2. Жорданова нормальная форма
10.3.Приведение матрицы к жордановой (нормальной) форме
Алгоритм приведения матрицы a к жордановой форме
11. Билинейные и квадратичные формы
Преобразование матрицы билинейной формы при переходе к новому базису. Ранг билинейной формы
Приведение квадратичной формы к каноническому виду
Закон инерции квадратичных форм
Классификация квадратичных форм
Необходимое и достаточное условие знакоопределенности квадратичной формы
Необходимое и достаточное условие знакопеременности квадратичной формы
Необходимое и достаточное условие квазизнакопеременности квадратичной формы
Пример 9.2. 1) В пространстве V размерности 3 найти матрицу оператора гомотетии.
Решение. Выбираем произвольный базис e1, e2, e3, находим образы базисных векторов (e1) = ke1, (e2) = ke2, (e3) = ke3, а затем их координаты.
[(e1)] = ![]() ,
[(e2)] =
,
[(e2)] = ![]() ,
[(e3)] =
,
[(e3)] = ![]() .
.
Составляем
матрицу : M() = 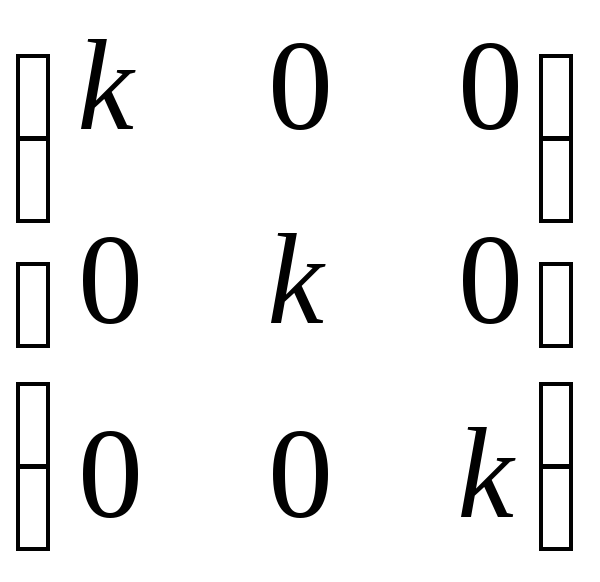 .
В
частности, получаем матрицы тождественного
и нулевого операторов: M() =
.
В
частности, получаем матрицы тождественного
и нулевого операторов: M() = 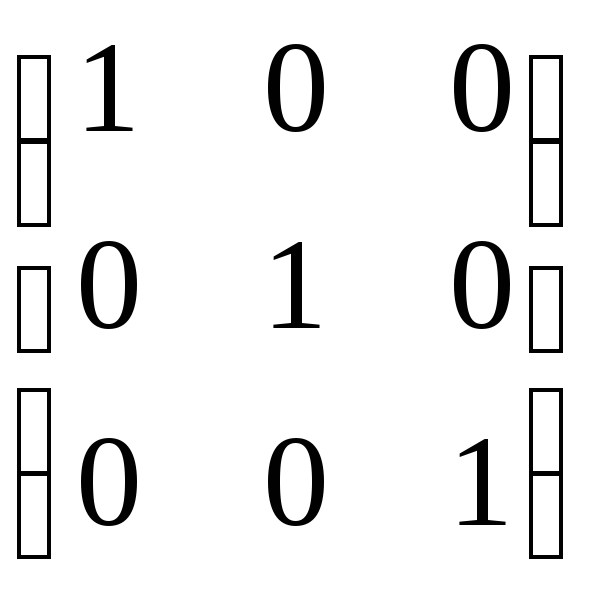 = Е,
M() =
= Е,
M() = 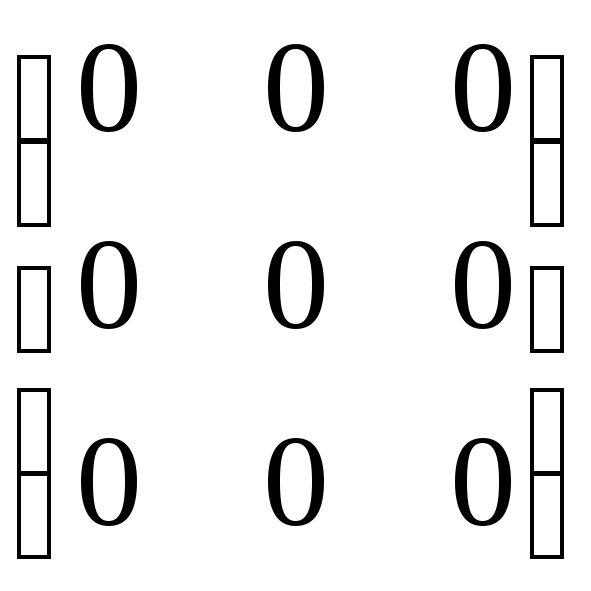 = О.
= О.
2) Найти матрицу оператора дифференцирования в пространстве R[x](3) в базисе e1 = 1, e2 = x, e3 = x2, e4 = x3.
Решение. Найдем образы базисных векторов, их координаты и составим матрицу линейного оператора.
(e1) = 0, (e2) = 1, (e3) = 2x, (e4) = 3x2;
[(e1)] = ![]() ,
[(e2)] =
,
[(e2)] = ![]() ,
[(e3)] =
,
[(e3)] = ![]() ,[(e4)] =
,[(e4)] = ![]() ;M() =
;M() = 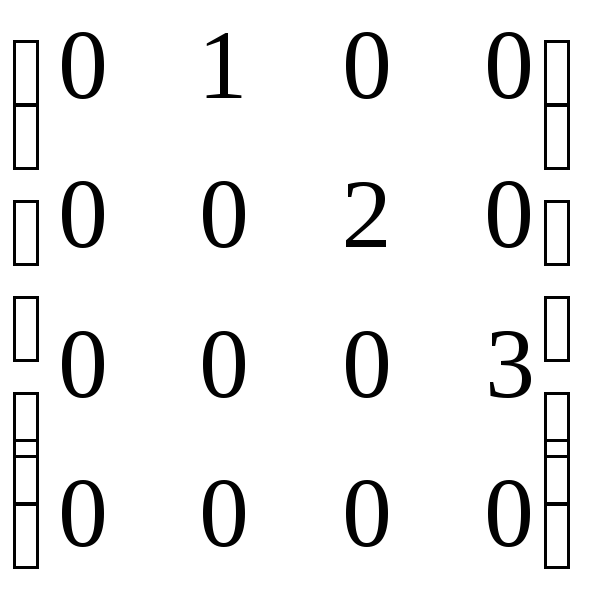 .
.
9.2. Матрица линейного оператора Связь между координатами вектора и координатами его образа
В
пространстве
V
задан линейный оператор ,
а также в некотором базисе e1,
e2,
…, en
найдена его матрица
M().
Пусть в этом базисе найдены координаты
векторов x
и
(x):
[x] = ![]() ,
[(x)] =
,
[(x)] = ![]() .
Установим связь
между
столбцами [x]
и [(x)].
.
Установим связь
между
столбцами [x]
и [(x)].
(х) = y1e1 + y2e2 + … + ynen;
(х) = (x1e1 + x2e2 + … + xnen) = x1(e1) + x2(e2) + … + xn(en) = = x1(11e1 + 21e2 + … + n1en) + x2(12e1 + 22e2 + … + n2en) + … … + xn(1ne1 + 2ne2 + … + nnen) = (x111 + x212 + … + xn1n)e1 + (x121 + x222 + … + xn2n)e2 + … + (x1n1 + x2n2 + … + xnnn)en.
Вектор (x) разложен по векторам базиса e1, e2, …, en двумя способами, но в силу единственности такого разложения коэффициенты при одинаковых базисных векторах можно приравнять:
y1 = x111 + x212 + … + xn1n,
y2 = x121 + x222 + … + xn2n,
…………………………………..
yn = x1n1 + x2n2 + … + xnnn.
Полученные равенства можно записать в матричной форме:
![]() =
= 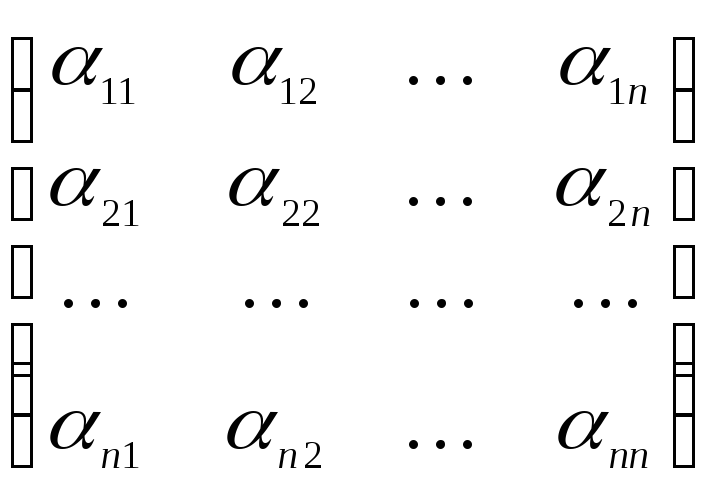
![]() или [(x)] = M()[x].
или [(x)] = M()[x].
Теорема 9.2 (о матрице линейного оператора). Если для любого вектора x из пространства V выполняется матричное равенство [(x)] = В[x], то матрица B является матрицей линейного оператора .
Матрицы линейного оператора в различных базисах
Зададим в пространстве V два базиса e1, e2, …, en и e'1, e'2, …, e'n (старый и новый). Связь между двумя базисами выражается матрицей перехода T . В пространстве V действует линейный оператор . В каждом из этих базисов для линейного оператора найдены матрицы. Обозначим их, соответственно, M()и M'() и установим, как одна из них выражается через другую.
Пусть [x] и [x]' столбцы координат произвольного вектора x в старом и новом базисах соответственно, связь между которыми дает формула: [x] = Т[x]'. Вектор (x) – образ вектора х, пусть [(x)] и [(x)]' – столбцы координат вектора (x) в старом и новом базисах соответственно. Имеет место формула [(x)] = Т[(x)]'.
Вставим в соотношение [(x)] = M()[x] выражение старых координат векторов x и (x) через новые: Т[(x)]' = M()Т[x]'. Умножим полученное равенство слева на матрицу T –1 и получим [(x)]' = (T –1M()Т )[x]'.
Из теоремы 9.2 о матрице линейного оператора следует, что
M '() = T –1M()Т .
Пример 9.3. 1) Линейный оператор в базисе e1, e2 задан формулой (x) = (3х1 – х2, х1 + х2). Найти матрицу этого линейного оператора в базисе e'1, e'2 если e'1 = 3е1 + 2е2, e'2 = 4е1 + 3е2.
Решение. Сначала составим матрицу линейного оператора в старом базисе, для чего нужны координаты образов базисных векторов:
(e1) = (1, 0) = (31 – 0, 1 + 0) = (3, 1),
(e2) = (0, 1) = (30 – 1, 0 + 1) = (–1, 1),
M() = ![]() .
.
Затем находим матрицу перехода T и обратную к ней матрицу T –1:
e'1 = 3е1 + 2е2 e'1 = (3, 2),
e'2 = 4е1 + 3е2 e'2 = (4, 3),
T = ![]() тогда T
–1 =
тогда T
–1 = ![]() .
.
Используем формулу и находим M '() = T –1M()Т :
M '() = ![]()
![]()
![]() =
= ![]()
![]() =
= ![]() .
.
Ответ:
M '() = ![]() .
.
2) Линейный оператор в базисе e1, e2 задан формулой (x) = (2х1 + 4х2, –х1 – 3х2). Найти матрицу этого линейного оператора в базисе e'1, e'2 если e'1 = –4е1 + е2, e'2 = –е1 + е2.
Решение. По рассмотренному алгоритму найдем M() и M '().
Ответ:
M() = ![]() ,
M '() =
,
M '() = ![]() .
.
Отметим, что в новом базисе матрица линейного оператора приняла диагональный вид.
9.3. Подобные матрицы
Рассмотрим множество Рnn квадратных матриц порядка n с элементами из произвольного поля P.
Введем на этом множестве отношение между матрицами – отношение подобия.
Определение 9.4. Матрица A называется подобной матрице B, если существует обратимая матрица T такая, что А = T –1BT. Обозначение А B.
Свойства отношения подобия матриц
Рефлексивность. Любая матрица подобна сама себе, т. е. А А.
Симметричность. Если матрица A подобна B, то и B подобна A, т. е. А B B А.
Транзитивность. Если матрица A подобна B и матрица B подобна C, то матрица A подобна матрице C, т. е. А B и B С то А С.
Множество Рnn рассмотренным отношением разбивается на подмножества (классы), в каждое из которых входят матрицы, подобные между собою. Общих элементов у полученных подмножеств нет.
Вспомним связь между матрицами линейного оператора в различных базисах: M '() = T–1M()Т . Очевидно, что M '() M(). Сформулируем правило: матрицы одного и того же линейного оператора в различных базисах подобны между собою.
9.4. Действия над линейными операторами
В векторном пространстве V над произвольным полем P заданы линейные операторы и .
1. Сложение линейных операторов.
Определение 9.5. Суммой линейных операторов и называется отображение, обозначаемое + ψ и действующее по правилу: ( + ψ)(x) = (x) + ψ(x), для х V.
Теорема 9.3. Сумма линейных операторов является линейным оператором.
Доказательство. Проверим два свойства.
1. ( + ψ)(x + y) = (x + y) + ψ(x + y) =(x) + (y) + ψ(x) + ψ(y) = (x) + + ψ(x) + (y) + ψ(y) = ( +ψ)(x) + ( + ψ)(y).
2. ( + ψ)(λx) = (λx) + ψ(λx) = λ(x) + λψ(x) = λ( + ψ)(x).