Файл: Линейная Алгебра от 2 октября 2013.doc

Определение 3.12. Суммой двух матриц А = (a_ij) и B = (b_ij), где i = 1, 2, …, m, j = 1, 2, …, n называется матрица С = (с_ij) для которой с_ij = a_ij + b_ij, где i = 1, 2, …, m, j = 1, 2, …, n. Обозначение: С = А + B.

Иначе говоря: сложение матриц производится поэлементно.

Пример 3.1. Для матриц А = и В = найти их сумму.

Решение. С = А + B = + = .

Свойства сложения матриц

коммутативность:  А, В : А + В = В + А;
ассоциативность:  А, В, С : (А + В) + С = А + (В + С);
 А, А + О = А, где О – нулевая матрица;
 А,  –А : А + (–А) = О, (–А) – матрица, противоположная матрице А.

Замечание 3.1. Пусть А = (a_ij) тогда –А = (–a_ij), где элемент –a_ij – противоположный элементу a_ij для любых индексов i и j, при этом матрица –А называется противоположной к матрице А.

Пример 3.2. Пусть А = тогда –А = .

3.2.2. Умножение матрицы на число

Определение 3.13. Произведением матрицы А = (a_ij) на действительной число k называется матрица С = (с_ij), для которой с_ij = ka_ij, где i = 1, 2, …, m, j = 1, 2, …, n. Обозначение: С = kА = kА, т. о. каждый элемент матрицы А умножают на действительное число k.

Пример 3.3. Пусть дано число k = –2 и матрица А = , тогда kА = (–2) = .

Свойства умножения матрицы на число

 А : 1А = А;
 α, β  R,  А : (αβ)А = α(βА) = β(αА);
 α  R,  А, В : α(А + В) = αА + αВ;
 α, β  R,  А : (α + β)А = αА + βА.

3.2.3. Умножение матриц

Определим умножение двух матриц; для этого необходимо ввести некоторые дополнительные понятия.

Определение 3.14. Матрицы А и В называются согласованными, если число столбцов матрицы А равно числу строк матрицы В.

Например матрицы А размерности m  n и В размерности n  p будут согласованными.

Обозначим строки матрицы А как А₁, А₂, …, А_m, а столбцы матрицы В как B¹, B², …, B^p. При этом в строке матрицы А столько же элементов, сколько в столбце матрицы В. Это условие позволяет умножать строку матрицы А на столбец матрицы В.

Умножим, например, А₁ на столбец B¹. Пусть А₁ = (а₁ а₂ … а_n), B¹ = тогда А₁B¹ = (а₁ а₂ … а_n) = а₁b₁ + а₂b₂ + … + а_nb_n.

Пример 3.4. Умножим строку (1 2 3 4) на столбец . (1 –2 3 4) = (13 + (–2)2 + 31 + 40) = (2).

Теперь можно определить умножение матриц.

Определение 3.15. Произведением согласованных матриц А размерности m  n и В размерности n  p называется матрица С = (с_ij) размерности m  p, для которой с_ij = А_iB^j, где i = 1, 2, …, m, j = 1, 2, …, p.

Обозначение: С = AB = .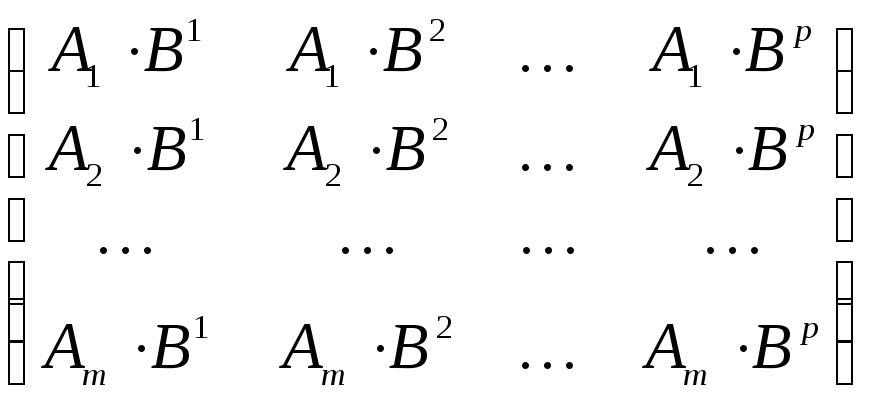

Пример 3.5. Найти произведение матриц АВ, где А = 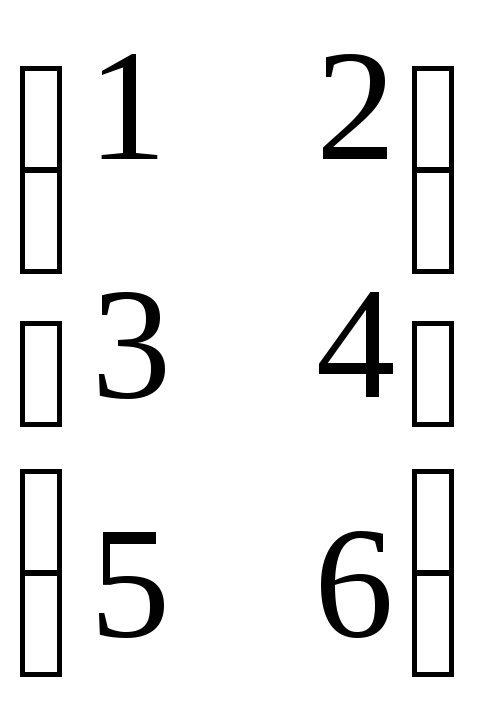, В = .

Решение. Матрицы А₃_₂ и В₂_₄ согласованы, значит можно найти произведение этих матриц АВ, результатом будет матрица размерности 3  4. АВ =  =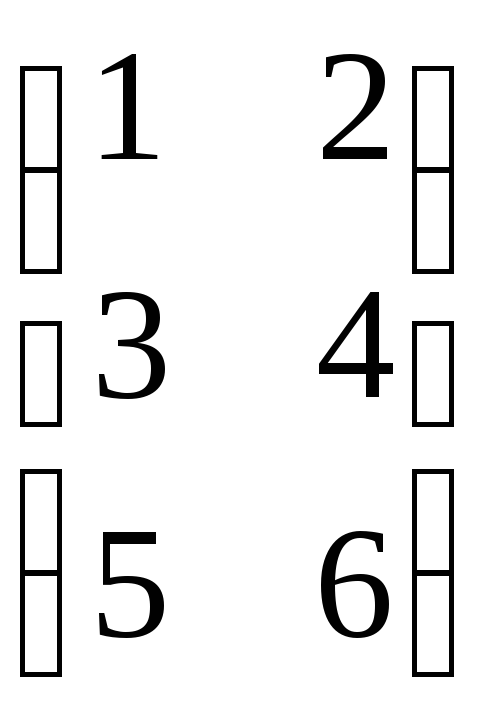

= =

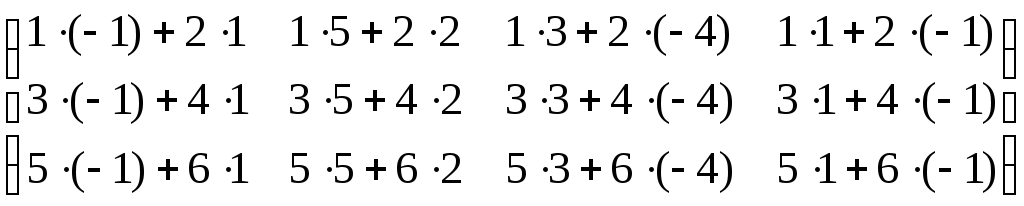Свойства умножения матриц

Умножение матриц не коммутативно: AB ≠ BA.

Продемонстрировать данное свойство можно на примерах.

Пример 3.6. а) Пусть даны две матрицы: А = и В = . Перемножим матрицы AB =  = = , получим матрицу размерности 2  1. Умножить матрицу В = В₂_₁ на матрицу А = А₂_₂ нельзя, так как эти матрицы не согласованные. Т. о. свойство коммутативности для умножения двух матриц не выполняется.

б) Возьмем две матрицы так, чтобы А и В были согласованы и чтобы также В и А были согласованные. Проверим, что при данных условиях свойство коммутативности также не выполняется. Пусть А = А₂_₃ = и В = В₃_₂ = 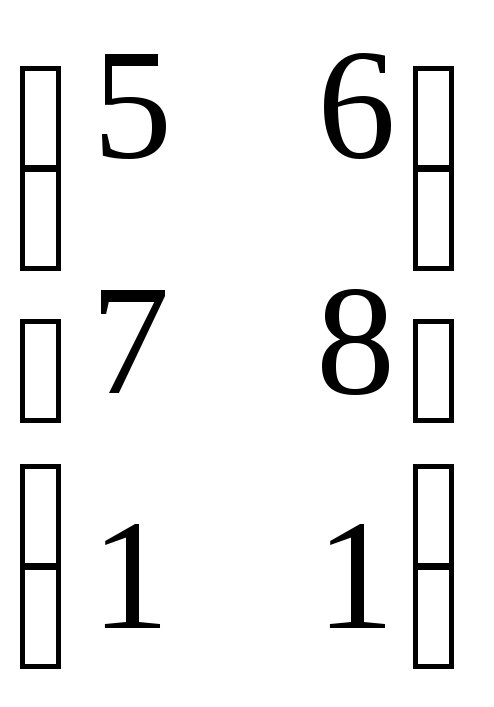, найдем их произведения.

AB = 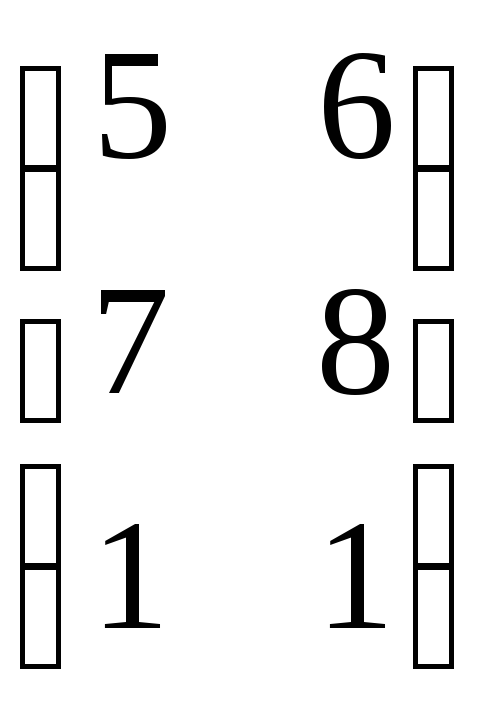 = = С₂_₂;

ВА = 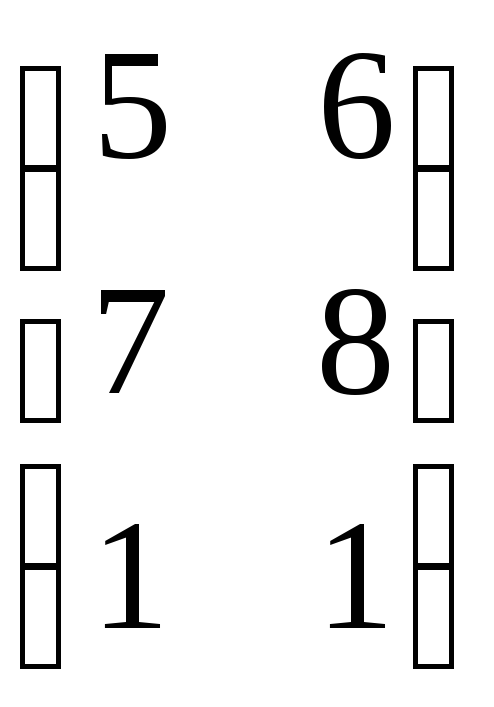 = = С₃_₃.

Ассоциативность: (AB)С = А(ВС).
Для любой квадратной матрицы А и согласованной с ней единичной матрицы Е справедливо равенство: AЕ = ЕA.
Дистрибутивный закон умножения матриц относительно сложения матриц:  А, В, С : (A + B)С = (АС) + (ВС) и A(B + С) = (АВ) + (АС).

Пример 3.7. Пусть даны матрицы А = , В = и С = проверим справедливость свойства 4.

(A + B)С = +  =  = ;

(АС) + (ВС) =  +  = + = .

 k  R,  А, В : k(АВ) = (kА)В = А(kВ).

3.3. Транспонирование матриц

Определение 3.16. Матрица А^t, полученная из данной заменой каждой ее строки столбцом с тем же номером, называется транспонированной к данной матрице А.

Если A – матрица размерности m  n, то А^t – матрица размерности n  m.

При транспонировании верны следующие равенства:

(А + В)^t = А^t + В^t;
(kA)^t = kА^t;
(AB)^t = В^tА^t.

4. Определители квадратных матриц

4.1. Определители матриц второго и третьего порядка

Каждой квадратной матрице А порядка n ставится в соответствие число, которое называется определителем этой матрицы. Обозначение: , |A|, det A, .

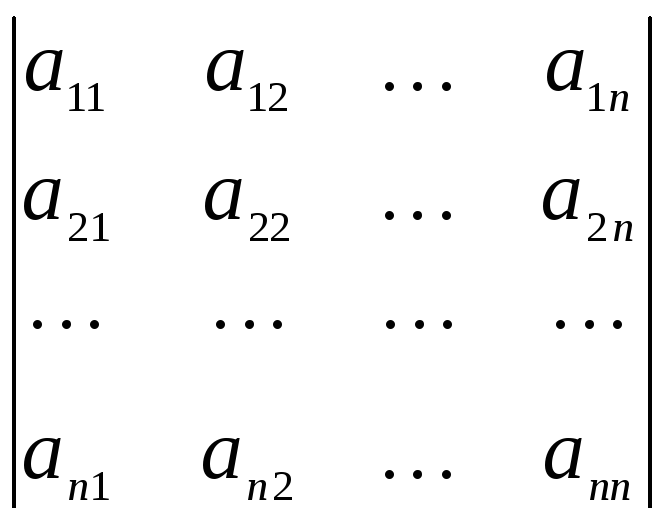Определение 4.1. Определителем матрицы первого порядка А = (а₁₁) называется число а₁₁.

Пример 4.1. Например: если дана матрица первого порядка А = (3), то определитель этой матрицы |A| = 3.

Определение 4.2. Определителем матрицы второго порядка А = 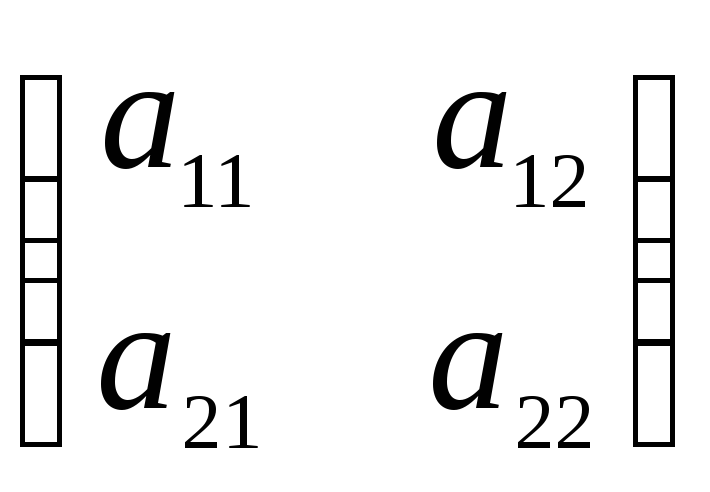называется число, которой находится по формуле: |A| = = а₁₁а₂₂ – а₁₂а₂₁.

Пример 4.2. Если дана матрица второго порядка А = , то определитель этой матрицы |A| = = 14 – 23 = 4 – 6 = –2.

Определение 4.3. Определителем матрицы третьего порядка А = 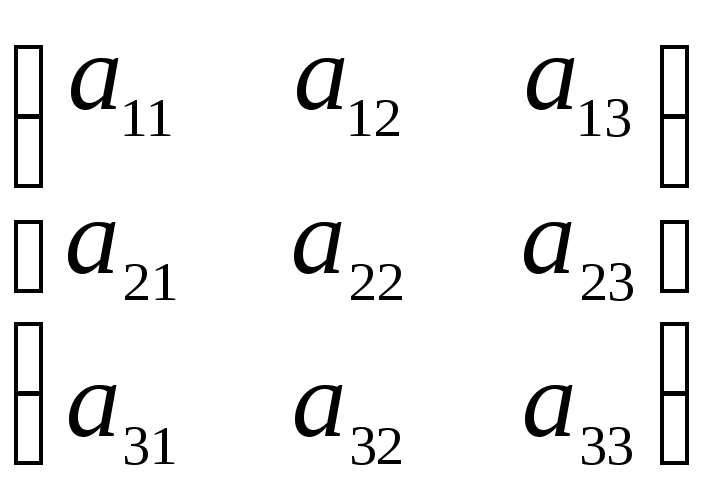называется число, которой находится по формуле: |A| = а₁₁а₂₂а₃₃ + а₁₂а₃₁а₂₃ + а₂₁а₁₃а₃₂ – а₁₃а₂₂а₃₁ – а₁₁а₃₂а₂₃ – а₃₃а₂₁а₁₂.

Это число состоит из шести слагаемых, в каждое слагаемое в качестве множителей входит по одному элементу из каждой строки и каждого столбца. Для запоминания формулы можно воспользоваться наглядным правилом знаков для выписывания произведений, входящих в разложение определителя третьего порядка. Схема на рис. 4.1 называется правилом треугольника или правилом Саррюса^¹⁰.