Файл: Линейная Алгебра от 2 октября 2013.doc

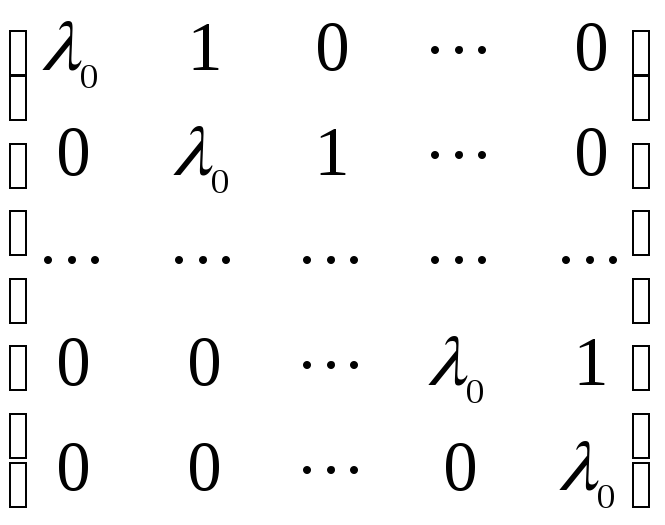на ее главной диагонали стоит одно и то же число ₀, а на параллельной ей сверху диагонали стоят единицы, все же остальные элементы равны нулю. Например: (₀), , 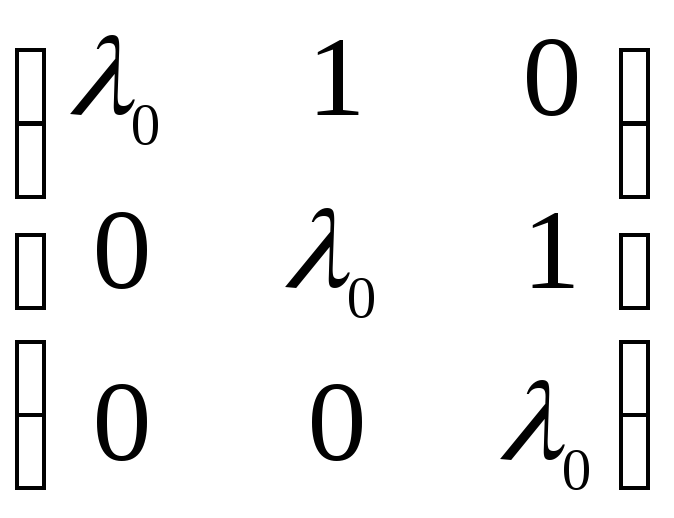– жордановы клетки первого, второго и третьего порядков соответственно.

Определение 10.6. Жордановой матрицей порядка n называется матрица порядка n, имеющая вид: J = . В ней вдоль главной диагонали идут жордановы клетки J₁, J₂, …, J_s некоторых порядков, не обязательно различных, и относящиеся к некоторым числам, тоже не обязательно различным. Все места вне этих клеток заняты нулями. При этом s ≥ 1, то есть одна жорданова клетка порядка n так же считается жордановой матрицей и s ≤ n.

Замечание. Говорят, что матрица J имеет нормальную жорданову форму. Диагональная матрица является частным случаем жордановой матрицы, у нее все клетки имеют порядок 1.

10.3.Приведение матрицы к жордановой (нормальной) форме

Теорема 10.3. Жорданова нормальная форма определяется для матрицы однозначно с точностью до порядка расположения жордановых клеток на главной диагонали.

Приведем матрицу A(λ) = A – λE к каноническому виду с помощью элементарных преобразований.

A – λE = .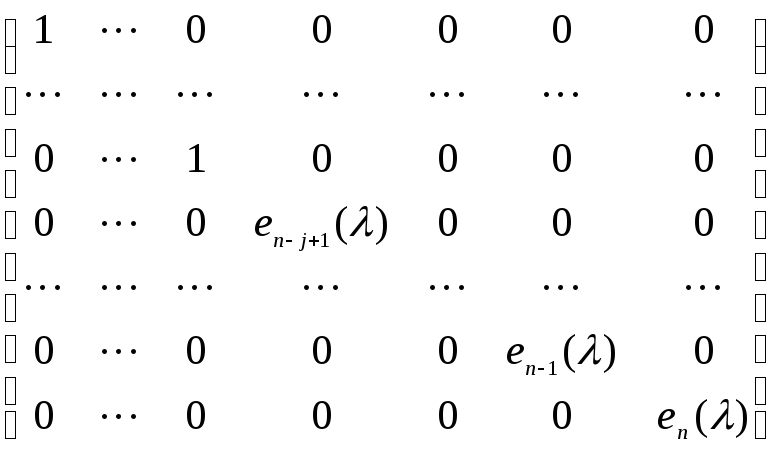

Отличные от единицы многочлены e_n_–_j₊₁(λ), …, e_n_–1(λ), e_n(λ) называют инвариантными множителями матрицы A(λ). Среди них нет многочленов равных нулю, сумма степеней всех этих многочленов равна n, и все они раскладываются на линейные множители над множеством комплексных чисел. Пусть e_n_–_j₊₁(λ) раскладывается в произведение следующих множителей: , , …, . Назовем эти множители элементарными делителями многочлена e_n_–_j₊₁(λ).

Определение 10.7. Элементарными делителями матрицы A(λ) называются элементарные делители всех многочленов e_n_–_j₊₁(λ), …, e_n_–1(λ), e_n(λ).

Выпишем жорданову матрицу J порядка n, составленную из жордановых клеток определяемых следующим образом: каждому элементарному делителю матрицы A(λ) ставим в соответствие жорданову клетку порядка k_ij, относящуюся к числу _i.

Пусть для некоторой матрицы порядка 9 характеристическая матрица A – λE приведена к каноническому виду.

A – λE = .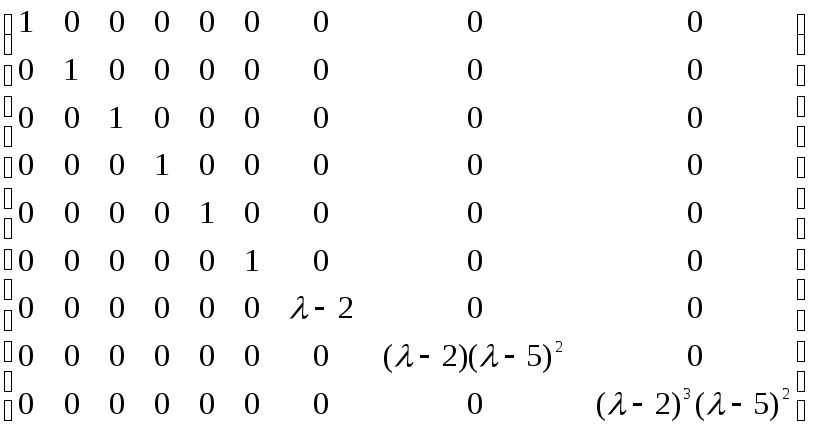

e₁ = e₂ = e₃ = e₄ = e₅ = e₆ = 1, e₇ =  – 2, e₈ = ( – 2)( – 5)², e₉ = ( – 2)³( – 5)² – инвариантные множители матрицы A – λE, ( – 2), ( – 2), ( – 5)², ( – 2)³, ( – 5)² – элементарные делители матрицы A – λE.

Получаем: две клетки порядка 1, относящиеся к числу 2, две клетки порядка 2, относящиеся к числу 5 , одну клетку порядка 3, относящуюся к числу 2, Выпишем жорданову форму матрицы A

Алгоритм приведения матрицы a к жордановой форме

Составить характеристическую матрицу A – λE.
Привести эту матрицу к канонической форме с помощью элементарных преобразований.
Разложить диагональные многочлены на линейные множители.
Найти элементарные делители и по ним выписать жорданову форму матрицы A.

Для того чтобы заданная матрица была подобна диагональной матрице, необходимо и достаточно, чтобы все элементарные делители ее характеристической матрицы были первой степени.

Пример 10.4. Привести к жордановой форме матрицу A = .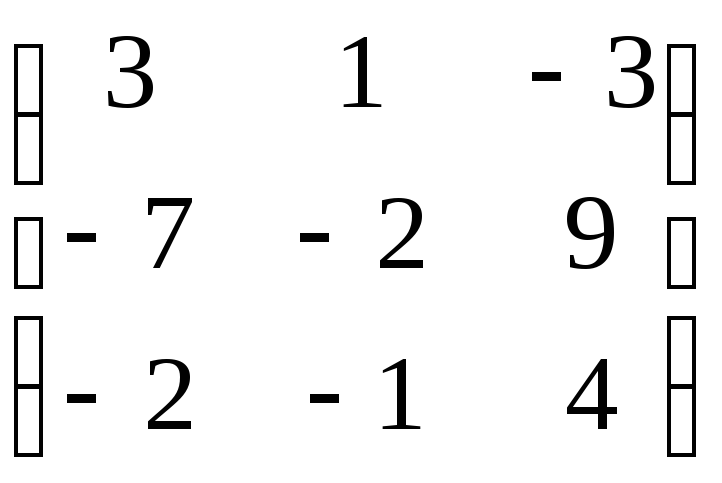

Решение. с помощью элементарных преобразований приводим матрицу A –λE к следующему виду: A –λE = 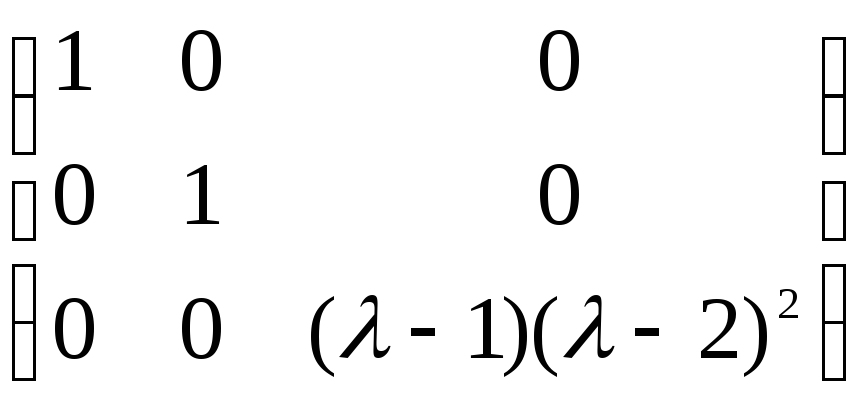  …  . Инвариантные множители этой матрицы: e₁ = 1, e₂ = 1, e₃ = ( – 1)( – 2)²; элементарные делители будут ( – 1), ( – 2)².

По найденным элементарным делителям выписываем жорданову форму исходной матрицы .

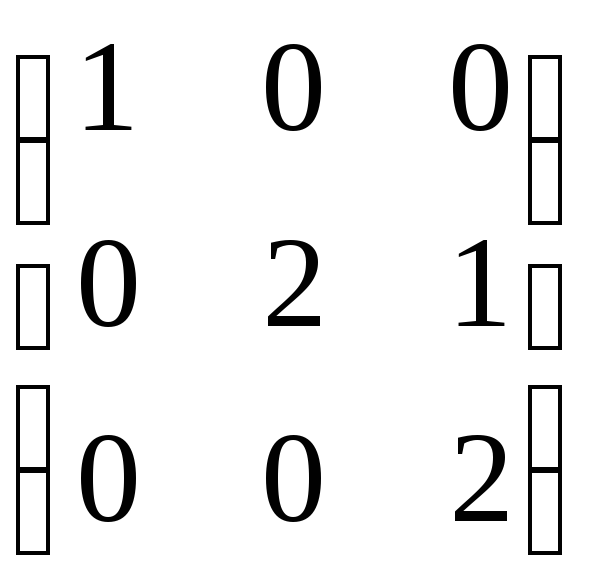11. Билинейные и квадратичные формы

11.1. Билинейные формы

Определение 11.1. Билинейной формой называется функция (отображение) f: V  V  R (или C), где V – произвольное векторное пространство, и для любых векторов x, y  V и любого числа λ  R (или C) выполняются соотношения

f(x + y, z) = f(x, y) + f(z, y),

f(x, y + z) = f(x, y) + f(x, z),

f(λx, y) = λf(x, y),

f(x, λy) = λf(x, y).

Обозначим число, получаемое в результате отображения пары векторов x и y, как A(x, y) .

Определение 11.2. Билинейная форма A(x, y) называется симметрической, если для любых x, y  V выполняется: A(x, y) = A(y, x).

Определение 11.3. Билинейная форма A(x, y) называется кососимметрической, если для любых x, y  V выполняется: A(x, y) = –A(y, x).

Свойства билинейных форм

Любую билинейную форму можно представить в виде суммы симметричной кососимметричной форм.

При выбранном базисе e₁, e₂, …, e_n в векторном пространстве V любая билинейная форма A однозначно определяется матрицей

A(е) = ,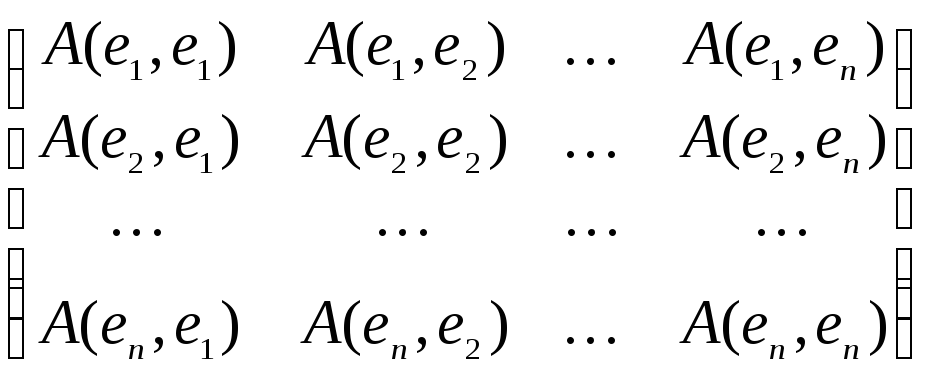

так, что для любых x = x₁e₁ + x₂e₂ + … + x_ne_n, y = y₁e₁ + y₂e₂ + … + y_ne_n;

A(x, y) = (x₁ x₂ … x_n)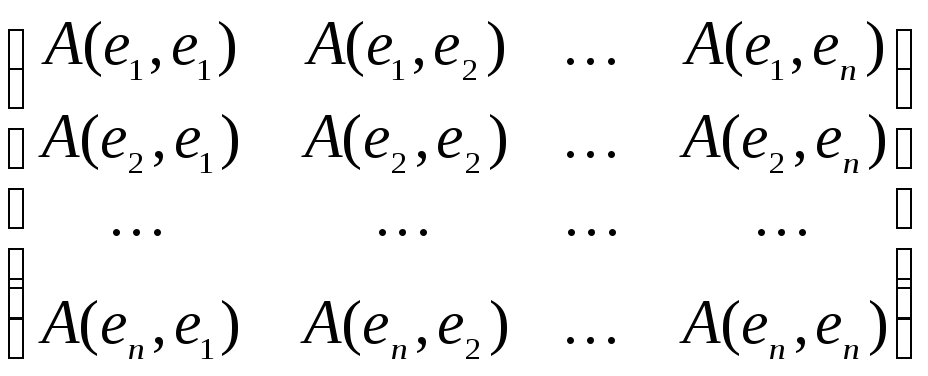, то есть

A(x, y) = ,где А_ij = A(e_i, e_j). (1)

Вид (1) назовем общим видом билинейной формы в n-мерном векторном пространстве.

Замечание. Если билинейная форма A(x, y) симметрическая, то и матрица (A_ij) будет симметрической, то есть A_ij = A_ji для i, j = 1, 2, …, n. Если билинейная форма A(x, y) кососимметрическая, то и матрица (A_ij) будет кососимметрической, то есть A_ij = –A_ji для i, j = 1, 2, …, n.

Преобразование матрицы билинейной формы при переходе к новому базису. Ранг билинейной формы

Пусть в векторном пространстве V заданы два базиса e = {e₁, e₂, …, e_n} и f = {f₁, f₂, …, f_n}. Пусть A(e) = (а_ij) и A(f) = (b_ij) – матрицы билинейной формы A в указанных базисах.

Теорема 11.1. Матрицы A(e) и A(f) билинейной формы A(x, y) в базисах {e} и {f} связаны соотношением

A(f) = C^tA(e)C, (),

где C – матрица перехода от базиса {e} к базису {f}, а C^t –транспонированная матрица C.

Следствие. Ранг матрицы A(f) равен рангу матрицы A(e).

Это утверждение следует из равенства (): так как С – матрица перехода от одного базиса к другому, то матрица С и матрица C^t– невырожденные, поэтому умножение на них матрицы A(e) не меняет ее ранга.

Определение 11.4. Рангом билинейной формы, заданной в конечномерном векторном пространстве V , называется ранг матрицы этой формы в произвольном базисе пространства V.

Определение 11.5. Билинейная форма называется невырожденной, если ее ранг равен размерности пространства V и вырожденной, если ее ранг меньше размерности пространства V.

11.2. Квадратичные формы

Пусть A(x, y) – симметрическая билинейная форма, заданная на векторном пространстве V.

Определение 11.6. Квадратичной формой называется числовая функция одного векторного аргумента x, которая получается из билинейной формы A(x, y) при x = y.

Определение 11.7. Симметрическая билинейная форма A(x, y) называется полярной квадратичной форме A(x, x).

Пусть дана билинейная форма A(x, y) = , положим в ней x_i = y_j, тогда мы получим представление квадратичной формы A(x, x) в конечномерном векторном пространстве V с заданным базисом {e}: