Файл: Линейная Алгебра от 2 октября 2013.doc

Доказательство. Пусть а₁, а₂, …, а_n – произвольный базис евклидова пространства Е. Доказательство заключатся в описании алгоритма построения ортогонального базиса по данному базису. Этот алгоритм называется процессом ортогонализации. Пусть b₁ = a₁, b₁ ≠ 0 (т. к. а₁ ≠ 0). Положим b₂ = a₂ + ₁b₁. Подберем коэффициент ₁ так, чтобы b₂ ≠ 0 стал ортогонален b₁;

(b₁, b₂) = 0  (b₁, a₂ + ₁b₁) = 0  (a₂ + ₁b₁, b₁) = 0  (a₂, b₁) + ₁(b₁, b₁) = 0, т. к. b₁ ≠ 0, то (b₁, b₁) ≠ 0  ₁ = .Вектор b₂ не равен нулю, поскольку он является ненулевой линейной комбинацией линейно независимых векторов a₁ и a₂.

Положим, далее b₃ = a₃ + ₁b₁ + ₂b₂. Подберем ₁ и ₂ так, чтобы b₃ ≠ 0 оказался ортогонален b₁ и b₂, для чего должны выполняться условия (b₁, b₃) = 0, (b₂, b₃) = 0. Выполняя преобразования, получим, что ₁ = , ₂ = . Вектор b₃ не равен нулю, поскольку он является ненулевой линейной комбинацией векторов а₁, а₂, а₃.

Продолжая этот процесс, получим систему векторов b₁, b₂, …, b_n, и так как эти векторы ненулевые и попарно ортогональны, то по теореме 8.11 они линейно независимы, а значит образуют ортогональный базис.

Нормируя ортогональный базис b₁, b₂, …, b_n, получим ортонормированный базис n-мерного евклидова пространства:

e₁ = b₁, e₂ = b₂, …, e_n = b_n.

Пример 8.12. Применить процесс ортогонализации к векторам а₁ = (2, –2, –2, 2), а₂ = (3, –1, –1, 3), а₃ = (2, –2, 0, 4).

Решение. Это задание можно сформулировать так: по данному базису подпространства построить ортогональный базис.

b₁ = а₁, b₁ = (2, –2, –2, 2);

b₂ = a₂ + ₁b₁, ₁ = === –1.Тогда b₂ = a₂ – b₁ = (1, 1, 1, 1).

b₃ = a₃ + ₁b₁ + ₂b₂, ₁ = == –1,₂ = == –1.Тогда b₃ = a₃ – b₁ – b₂ = (–1, –1, 1, 1).

Скалярное произведение в ортонормированном базисе

Дан ортонормированный базис e₁, e₂, …, e_n евклидова пространства V. Поскольку (e_i, e_j) = 0 при i ≠ j и (e_i, e_i) = 1, то

(x, y) = (e_i, e_j) = x₁y₁ + x₂y₂ + … + x_ny_n.

Вывод: скалярное произведение векторов в ортонормированном базисе равно сумме произведений соответствующих координат.

Ортогональное дополнение подпространства

V – евклидово векторное пространство, L – его подпространство.

Определение 8.23. Говорят, что вектор а ортогонален подпространству L , если вектор а ортогонален любому вектору из подпространства L, т. е.

а  L  а  х,  х  L.

Определение 8.24. Ортогональным дополнением подпространства L называется множество L^* всех векторов, ортогональных подпространству L, то есть L^* = {x | x  L}.

Теорема 8.13. Ортогональное дополнение подпространства является подпространством.

Теорема 8.14. Прямая сумма подпространства L и его ортогонального дополнения L^* равна пространству V, т. е. L  L^* = V.

Пример 8.13. Найти ортогональное дополнение подпространства L, натянутого на векторы а₁ = (1, 1, 1, 1), а₂ = (–1, 1, –1, 1), а₃ = (2, 0, 2, 0).

Решение. Для того чтобы вектор x был ортогонален подпространству, необходимо и достаточно, чтобы он был ортогонален векторам системы образующих этого подпространства. Пусть х = (х₁, х₂, х₃, х₄), запишем условие ортогональности этого вектора векторам а₁, а₂, а₃: (х, а₁) = 0, (х, а₂) = 0, (х, а₃) = 0. В координатной форме эти условия представляют собою однородную систему линейных уравнений: 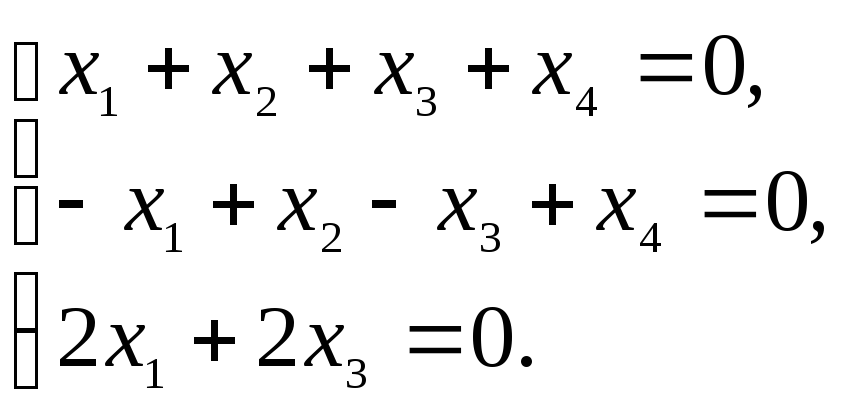Множество решений этой системы представляет собою подпространство L^*, ортогональное подпространству L.

Решая систему, получим фундаментальный набор решений: с₁ = (–1, 0, 1, 0), с₂ = (0, –1, 0, 1). Эти векторы образуют базис множества решений системы, то есть базис L^*, т. о. L^* = L(с₁,с₂), dim L^* = 2.

9. Линейные операторы

9.1. Основные понятия и способы задания линейных операторов

Дано V – векторное пространство над полем P, dim V = n.

Определение 9.1. Говорят, что задано отображение  множества V в себя, если каждому элементу x из V поставлен в соответствие единственный элемент y, тоже принадлежащий V. При этом приняты следующие обозначения и термины: : V  V, : х  y, (х) = y; элемент x – прообраз элемента y, y – образ x.

Определение 9.2. Линейным оператором пространства V называется отображение : V  V такое, что  a, b  V,    Р

(a + b) = (a) + (b),
(a) = (a).

Вместо «линейный оператор» говорят также «линейное отображение» или «отображение, сохраняющее операции сложения и умножения на элемент поля»

Пример 9.1. 1) В произвольном векторном пространстве V зададим отображение следующей формулой: (х) = kх. Это отображение является линейным оператором и называется оператором гомотетии.

Если k = 1, то отображение примет вид: (х) = 1. Его называют тождественным оператором и обозначают буквой : (х) = х.

Если k = 0, то получают нулевой оператор : (х) = o.

2) В пространстве V = R²^² оператор транспонирования задают формулой (А) = А^t, где А^t – матрица, транспонированная для матрицы А.

3) В пространстве V = R[x]₍__n₎ (многочленов степени, не превосходящей n) можно задать отображение , ставящее в соответствие произвольному многочлену его производную, т. е. : f(x)  f '(x), (f ) = f '. Покажем, что это отображение линейно:

(f + g) = (f + g)' = f ' + g ' = (f ) + (g),

(f ) = (f )' = (f )' = (f ).

Способы задания линейных операторов

Приведенные примеры не показывают, сколько в каждом векторном пространстве существует линейных операторов, каким способом их можно задавать. Ответом на эти вопросы является следующая теорема.

Теорема 9.1. Для того чтобы задать линейный оператор, достаточно задать образы базисных векторов.

Доказательство. Другими словами, если e₁, e₂, …, e_n– некоторый базис векторного пространства V над полем P, а b₁, b₂, …, b_n – произвольные векторы этого же пространства, то существует единственный линейный оператор, такой, что (e₁) = b₁, (e₂) = b₂, …, (e_n) = b_n.

Покажем, как найти образ произвольного вектора x. Разложим вектор x по базисным векторам и найдем его образ, используя свойства линейного отображения:

x = x₁e₁ + x₂e₂ + … + x_ne_n, где x_i  Р  (х) = (x₁e₁ + x₂e₂ + … + x_ne_n) = = (x₁e₁) + (x₂e₂) + … + (x_ne_n) = x₁(e₁) + x₂(e₂) + … + x_n(e_n) = = x₁b₁ + x₂b₂ + … + x_nb_n. Теорема доказана.

Пусть в векторном пространстве V задан линейный оператор , т. е. указаны образы базисных векторов (e₁), (e₂), …, (e_n). Разложим эти векторы по векторам базиса:

(e₁) = ₁₁e₁ + ₂₁e₂ + … + _n₁e_n,

(e₂) = ₁₂e₁ + ₂₂e₂ + … + _n₂e_n,

…………………………………..…..

(e_n) = ₁_ne₁ + ₂_ne₂ + … + _nne_n.

Используем координаты образов базисных векторов.

Определение 9.3. Матрицей линейного оператора в данном базисе называется матрица, составленная из координат образов базисных векторов, записанных в столбцы.

M(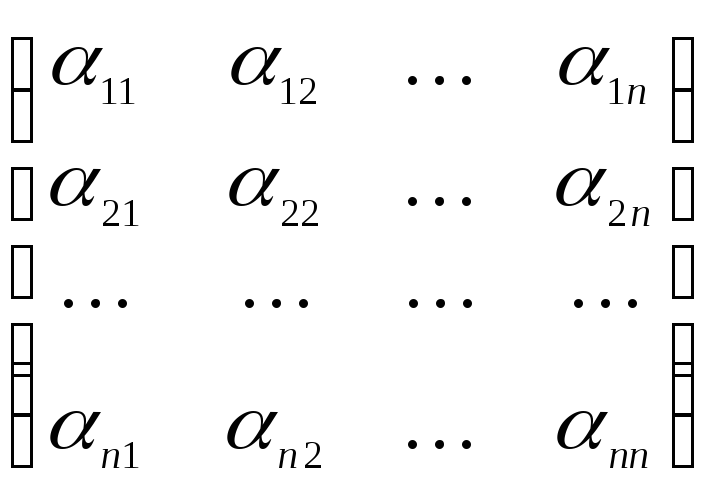) = , M()  Рⁿ^ⁿ.

Если зафиксировать базис пространства V, то каждому линейному оператору  ставится в соответствие единственная квадратная матрица порядка:   M().

Верно и обратное: по произвольной квадратной матрице A единственным образом можно задать линейный оператор , взяв за координаты образов базисных векторов столбцы матрицы A.