ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 11.08.2024
Просмотров: 581
Скачиваний: 0
СОДЕРЖАНИЕ
Т. Н. Матыцина е. К. Коржевина линейная алгебра
1.1. Множества и их элементы. Способы задания множеств
1.2. Подмножества. Диаграммы Эйлера – Венна
1.3. Операции над множествами и их свойства
2. Пересечение (или произведение).
4. Декартовое произведение (или прямое произведение).
Свойства операций над множествами
1.4. Метод математической индукции
Операции над комплексными числами
Геометрическая интерпретация комплексных чисел
Тригонометрическая форма комплексного числа
Действия над комплексными числами в тригонометрической форме
4. Извлечение корня n-ой степени.
Показательная форма комплексного числа
Способы задания бинарных отношений
Операции над бинарными отношениями
2.2. Свойства бинарных отношений
2.3. Отношение эквивалентности
3. Матрицы и действия над ними
3.2. Основные операции над матрицами и их свойства
3.2.1. Сложение однотипных матриц
3.2.2. Умножение матрицы на число
4. Определители квадратных матриц
4.1. Определители матриц второго и третьего порядка
4.2. Определитель матрицы n-го порядка
4.4. Практическое вычисление определителей
5. Ранг матрицы. Обратная матрица
5.2. Нахождение ранга матрицы методом окаймления миноров
5.3. Нахождение ранга матрицы с помощью элементарных преобразований
5.4. Понятие обратной матрицы и способы ее нахождения
Алгоритм нахождения обратной матрицы
Нахождение обратной матрицы с помощью элементарных преобразований
6.1. Основные понятия и определения
6.2. Методы решения систем линейных уравнений
6.3. Исследование системы линейных уравнений
6.4. Однородные системы линейных уравнений
Свойства решений однородной системы линейных уравнений
Фундаментальный набор решений однородной системы линейных уравнений
7. Арифметическое n-мерное векторное пространство
7.2. Линейная зависимость и независимость системы векторов
Свойства линейной зависимости системы векторов
Две теоремы о линейной зависимости
7.3. Базис и ранг системы векторов
8. Векторные (линейные) пространства
8.1. Определение векторного пространства над произвольным полем.
Простейшие свойства векторных пространств
Линейная зависимость и независимость системы векторов
8.2. Подпространства. Линейные многообразия
Пересечение и сумма подпространств
8.3. Базис и размерность векторного пространства
8.3.1. Конечномерные векторные пространства
Базис конечномерного векторного пространства
8.3.2. Базисы и размерности подпространств
8.3.3. Координаты вектора относительно данного базиса
8.3.4. Координаты вектора в различных базисах
8.4 Евклидовы векторные пространства
Скалярное произведение в координатах
Скалярное произведение в ортонормированном базисе
Ортогональное дополнение подпространства
9.1. Основные понятия и способы задания линейных операторов
Способы задания линейных операторов
9.2. Матрица линейного оператора Связь между координатами вектора и координатами его образа
Матрицы линейного оператора в различных базисах
Свойства отношения подобия матриц
9.4. Действия над линейными операторами
1. Сложение линейных операторов.
Свойства сложения линейных операторов
9.5. Ядро и образ линейного оператора
9.6. Обратимые линейные операторы
9.7. Собственные векторы линейного оператора
9.7.1. Свойства собственных векторов
9.7.2. Характеристический многочлен матрицы
9.7.3. Нахождение собственных векторов линейного оператора
9.7.4. Алгоритм нахождения собственных векторов линейного оператора
9.7.5.Условия, при которых матрица подобна диагональной матрице
10. Жорданова нормальная форма матрицы линейного оператора
10.2. Жорданова нормальная форма
10.3.Приведение матрицы к жордановой (нормальной) форме
Алгоритм приведения матрицы a к жордановой форме
11. Билинейные и квадратичные формы
Преобразование матрицы билинейной формы при переходе к новому базису. Ранг билинейной формы
Приведение квадратичной формы к каноническому виду
Закон инерции квадратичных форм
Классификация квадратичных форм
Необходимое и достаточное условие знакоопределенности квадратичной формы
Необходимое и достаточное условие знакопеременности квадратичной формы
Необходимое и достаточное условие квазизнакопеременности квадратичной формы
Операции над бинарными отношениями
Бинарные отношения – это множества упорядоченных пар. Следовательно, над ними можно выполнять любые теоретико-множественные операции, в частности, операции объединения и пересечения. Определим еще две операции над отношениями.
Определение 2.7. Обратным к отношению P A B (или инверсией) называется множество P–1, подмножество прямого произведения B A такое, что P–1 = {(y, x) | (x, y) P}.
Пример 2.6. Пусть P = {(a, 1), (b, 2), (c, 3), (d, 4), (e, 5)}. Тогда P–1 = {(1, a), (2, b), (3, c), (4, d), (5, e)}.
Определение 2.8.
Композицией
(или
суперпозицией)
отношений
P A B
и Q B C
называется множество P![]() Q = {(x,
y)
| x A,
y C,
( z B)
: (x,
z) P,
(z,
y) Q},
рис. 2.4.
Q = {(x,
y)
| x A,
y C,
( z B)
: (x,
z) P,
(z,
y) Q},
рис. 2.4.
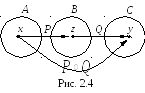
Пример 2.7.
Если
P = {(a,
b),
(b,
c),
(b,
d),
(a,
d),
(c,
a)},
Q = {(b,
d),
(c, a),
(d,
c)},
то
P![]() Q = {(a,
d),
(b,
a),
(b,
c),
(a,
c)}
и
Q
Q = {(a,
d),
(b,
a),
(b,
c),
(a,
c)}
и
Q![]() P = {(c,
b),
(c,
d),
(d, a)}.
P = {(c,
b),
(c,
d),
(d, a)}.
Утверждение 2.1. Для любых бинарных отношений P, Q и R выполняются следующие свойства:
(P–1)–1 = Р;
(P
 Q)–1 = Q–1
Q)–1 = Q–1 P–1;
P–1;(P
 Q)
Q) R = P
R = P (Q
(Q R).
R).
2.2. Свойства бинарных отношений
Пусть бинарное отношение Р задано на непустом множестве А, т. е. Р А2.
Определение 2.9. Бинарное отношение P на множестве А называется рефлексивным, если для любого элемента х из множества А пара (х, х) Р.
Другими словами, отношение P рефлексивно тогда и только тогда, когда каждая вершина графа имеет петлю.
Примерами рефлексивных отношений являются отношение делимости на множестве целых чисел; отношение включения на булеане непустого множества; отношение быть одинаково направленными на множестве всех направленных лучей.
Пример 2.8. Выяснить обладает ли отношение R = {(m, n), (m, k), (m, m), (n, n), (k, n)}, заданный на множестве А = {m, n, k}, свойством рефлексивности.
Решение. Данное бинарное отношение R А2, не будет рефлескивным так как для k A пара (k, k) R.
Определение 2.10. Бинарное отношение P на множестве А называется антирефлексивным, если х А : (х, х) Р.
Отношение антирефлексивно тогда и только тогда, когда ни одна вершина графа не имеет петли.
Например, отношение неравенства на некотором числовом множестве, отношение перпендикулярности на множестве всех прямых евклидовой плоскости являются антирефлексивными.
Пример 2.9. Выяснить обладает ли отношение R = {(x, y) | x, y R : x + y = 2}, свойствами рефлексивности и антирефлексивности.
Решение. Имеем пара (1, 1) R и (2, 2) R, следовательно данное бинарное отношение R, не является рефлескивным и не является антирефлексивным.
Определение 2.11. Бинарное отношение P на множестве А называется симметричным, если х, y А из того что пара (х, y) Р следует (y, x) Р.
Отношение симметрично тогда и только тогда, когда всякий раз вместе с ребром (х, y) граф содержит ребро (y, x).
Примерами симметричных отношений являются отношение равенства на некотором числовом множестве, отношение параллельности на множестве всех прямых евклидовой плоскости, отношение перпендикулярности на множестве всех прямых евклидовой плоскости.
Пример 2.10. Выяснить обладает ли отношение R = {(1, 2), (1, 3), (1, 1), (2, 3), (3, 1)}, заданное на множестве А = {1, 2, 3}, свойством симметричности.
Решение. Данное бинарное отношение R А2, не будет симметричным так как для пары (2, 3) R пара (3, 2) R.
Определение 2.12. Бинарное отношение P на множестве А называется антисимметричным, если х, y А из того, что пара (х, y) Р и (y, x) Р следует что x = y.
Отношение антисимметрично тогда и только тогда, когда вместе с каждым ребром (х, y) граф не содержит ребро (y, x). Граф антисимметричного отношения может содержать петли.
Примерами антисимметричных отношений являются отношение меньше (<) на множестве действительных чисел, отношение включения на булеане непустого множества.
Замечание 2.1. Если отношение не является симметричным, то это не означает, что оно антисимметрично. Например, отношение R = {(a, b), (b, a), (a, c)} на множестве A = {a, b, c} не симметрично, поскольку (a, c) R, а (c, a) R, и не антисимметрично, так как (a, b) R и (b, a) R, но a b. Диагональ непустого множества А (idA) является примером симметричного и антисимметричного отношения. Вообще, любое подмножество idA обладает одновременно свойствами симметричности и антисимметричности.
Определение 2.13. Бинарное отношение P на множестве А называется асимметричным, если х, y А если пара (х, y) Р, то (y, х) Р.
Отношение асимметрично тогда и только тогда, когда если граф содержит ребро (х, y), то он не содержит ребра (y, x).
Примерами асимметричных отношений являются отношение быть меньше (<) на числовом множестве. Отношение параллельности (||) на множестве прямых плоскости не является асимметричным, так как если а || b, то b || a и оно является симметричным.
Определение 2.14. Бинарное отношение P на множестве А называется транзитивным, если х, y, z А из того, что пара (х, y) Р и (y, z) Р следует что (х, z) Р.
Отношение транзитивно тогда и только тогда, когда вместе с каждой парой ребер (х, y) и (y, z) граф содержит ребро (х, z).
Например, отношение параллельности на множестве всех прямых евклидовой плоскости, отношение включения на булеане непустого множества являются транзитивными.
Утверждение 2.2. Пусть A ≠ и P A2. Тогда справедливы следующие соотношения:
P – рефлексивно idA P;
P – антирефлексивно P idA = ;
P – симметрично P = P–1;
P – антисимметрично P P–1 idA;
P – транзитивно P
 P P.
P P.
2.3. Отношение эквивалентности
Определение 2.15. Бинарное отношение на множестве А называется отношением эквивалентности, если оно рефлексивно, симметрично и транзитивно.
Отношение эквивалентности обычно обозначают символами или .
Примерами отношения эквивалентности являются отношение равенства на множестве действительных чисел, отношение параллельности на множестве прямых евклидовой плоскости, подобие треугольников на плоскости.
Определение 2.16. Пусть R – отношение эквивалентности на множестве А и а А. Классом эквивалентности, порожденным элементом а, называется множество a/R = [a]R = {х А | (х, а) R}.
Совокупность всех классов эквивалентности отношения R на множестве А обозначается через А/R.
Определение 2.17. Представителем класса эквивалентности называется любой элемент этого класса.
Определение 2.18. Пусть А – непустое множество. Фактор- множеством множества А по отношению эквивалентности R называется множество A/R всех классов эквивалентности.
Определение 2.19. Разбиением непустого множества А называется совокупность его непустых подмножеств, таких что объединение всех подмножеств есть множество А, а пересечение любых двух различных подмножеств есть пустое множество.
Теорема 2.1. Пусть R – отношение эквивалентности на непустом множестве А. Тогда фактор-множество A/R является разбиением множества А.
Доказательство.
Так как отношение R
рефлексивно, то для любого a A
имеем (а,
а) R.
Это значит, что каждый элемент a
множества
А
принадлежит классу эквивалентности
a/R.
Итак, имеем семейство непустых классов
a/R
(a/R
содержит по крайней мере один элемент
a)
и
![]() = A.
Осталось доказать, что пересечение
любых двух различных классов пусто. Для
этого достаточно показать, что классы
эквивалентности, имеющие хотя бы один
общий элемент, совпадают. Пусть a/R
и b/R
– классы эквивалентности, имеющие общий
элемент c.
Тогда (с, а) R
и (c,
b) R.
В силу симметричности отношения R
из
(c, a) R
следует (a,
c) R.
Пусть х
– любой элемент из a/R
, тогда (х, a) R.
Имеем, (х, a) R
и
(а, с) R.
Следовательно, в силу транзитивности
отношения R
(х, с) R.
Имеем, (х, с) R
и
(с, b) R.
Тогда (х, b) R,
так как отношение R
транзитивно. Следовательно, x b/R.
Таким образом, a/R b/R.
Аналогично доказывается, что b/R a/R.
Следовательно, a/R = b/R.
= A.
Осталось доказать, что пересечение
любых двух различных классов пусто. Для
этого достаточно показать, что классы
эквивалентности, имеющие хотя бы один
общий элемент, совпадают. Пусть a/R
и b/R
– классы эквивалентности, имеющие общий
элемент c.
Тогда (с, а) R
и (c,
b) R.
В силу симметричности отношения R
из
(c, a) R
следует (a,
c) R.
Пусть х
– любой элемент из a/R
, тогда (х, a) R.
Имеем, (х, a) R
и
(а, с) R.
Следовательно, в силу транзитивности
отношения R
(х, с) R.
Имеем, (х, с) R
и
(с, b) R.
Тогда (х, b) R,
так как отношение R
транзитивно. Следовательно, x b/R.
Таким образом, a/R b/R.
Аналогично доказывается, что b/R a/R.
Следовательно, a/R = b/R.