ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 11.08.2024
Просмотров: 592
Скачиваний: 0
СОДЕРЖАНИЕ
Т. Н. Матыцина е. К. Коржевина линейная алгебра
1.1. Множества и их элементы. Способы задания множеств
1.2. Подмножества. Диаграммы Эйлера – Венна
1.3. Операции над множествами и их свойства
2. Пересечение (или произведение).
4. Декартовое произведение (или прямое произведение).
Свойства операций над множествами
1.4. Метод математической индукции
Операции над комплексными числами
Геометрическая интерпретация комплексных чисел
Тригонометрическая форма комплексного числа
Действия над комплексными числами в тригонометрической форме
4. Извлечение корня n-ой степени.
Показательная форма комплексного числа
Способы задания бинарных отношений
Операции над бинарными отношениями
2.2. Свойства бинарных отношений
2.3. Отношение эквивалентности
3. Матрицы и действия над ними
3.2. Основные операции над матрицами и их свойства
3.2.1. Сложение однотипных матриц
3.2.2. Умножение матрицы на число
4. Определители квадратных матриц
4.1. Определители матриц второго и третьего порядка
4.2. Определитель матрицы n-го порядка
4.4. Практическое вычисление определителей
5. Ранг матрицы. Обратная матрица
5.2. Нахождение ранга матрицы методом окаймления миноров
5.3. Нахождение ранга матрицы с помощью элементарных преобразований
5.4. Понятие обратной матрицы и способы ее нахождения
Алгоритм нахождения обратной матрицы
Нахождение обратной матрицы с помощью элементарных преобразований
6.1. Основные понятия и определения
6.2. Методы решения систем линейных уравнений
6.3. Исследование системы линейных уравнений
6.4. Однородные системы линейных уравнений
Свойства решений однородной системы линейных уравнений
Фундаментальный набор решений однородной системы линейных уравнений
7. Арифметическое n-мерное векторное пространство
7.2. Линейная зависимость и независимость системы векторов
Свойства линейной зависимости системы векторов
Две теоремы о линейной зависимости
7.3. Базис и ранг системы векторов
8. Векторные (линейные) пространства
8.1. Определение векторного пространства над произвольным полем.
Простейшие свойства векторных пространств
Линейная зависимость и независимость системы векторов
8.2. Подпространства. Линейные многообразия
Пересечение и сумма подпространств
8.3. Базис и размерность векторного пространства
8.3.1. Конечномерные векторные пространства
Базис конечномерного векторного пространства
8.3.2. Базисы и размерности подпространств
8.3.3. Координаты вектора относительно данного базиса
8.3.4. Координаты вектора в различных базисах
8.4 Евклидовы векторные пространства
Скалярное произведение в координатах
Скалярное произведение в ортонормированном базисе
Ортогональное дополнение подпространства
9.1. Основные понятия и способы задания линейных операторов
Способы задания линейных операторов
9.2. Матрица линейного оператора Связь между координатами вектора и координатами его образа
Матрицы линейного оператора в различных базисах
Свойства отношения подобия матриц
9.4. Действия над линейными операторами
1. Сложение линейных операторов.
Свойства сложения линейных операторов
9.5. Ядро и образ линейного оператора
9.6. Обратимые линейные операторы
9.7. Собственные векторы линейного оператора
9.7.1. Свойства собственных векторов
9.7.2. Характеристический многочлен матрицы
9.7.3. Нахождение собственных векторов линейного оператора
9.7.4. Алгоритм нахождения собственных векторов линейного оператора
9.7.5.Условия, при которых матрица подобна диагональной матрице
10. Жорданова нормальная форма матрицы линейного оператора
10.2. Жорданова нормальная форма
10.3.Приведение матрицы к жордановой (нормальной) форме
Алгоритм приведения матрицы a к жордановой форме
11. Билинейные и квадратичные формы
Преобразование матрицы билинейной формы при переходе к новому базису. Ранг билинейной формы
Приведение квадратичной формы к каноническому виду
Закон инерции квадратичных форм
Классификация квадратичных форм
Необходимое и достаточное условие знакоопределенности квадратичной формы
Необходимое и достаточное условие знакопеременности квадратичной формы
Необходимое и достаточное условие квазизнакопеременности квадратичной формы
Обратным
ходом надо выразить главные неизвестные
через свободные. Для этого в столбцах,
содержащих ведущие элементы строк,
следует получить нули. Здесь это элемент
а13.
Прибавим к первому уравнению, умноженному
на 2, второе и выпишем получившуюся
матрицу коэффициентов:
![]() ,
а затем и сами уравнения:
,
а затем и сами уравнения:
 Из
этих уравнений получаем общее решение:
Из
этих уравнений получаем общее решение:

Найдем
какое-нибудь частное решение; пусть
х2 = 3,
х4 = 1,
тогда из общего решения получим значения
х1 = ![]() ,
и х1 = –2.
Таким образом, частное решение – вектор
а = (
,
и х1 = –2.
Таким образом, частное решение – вектор
а = (![]() ,
3, –2, 1).
,
3, –2, 1).
Ответ:
общее решение {(![]() ,
х2,
,
х2,
![]() ,
х4)},
где х2,
х4 R;
,
х4)},
где х2,
х4 R;
частное
решение, если х2 = 3,
х4 = 1,
то (![]() ,
3, –2, 1).
,
3, –2, 1).
6.3. Исследование системы линейных уравнений
Исследовать систему линейных уравнений – это значит, не решая систему, ответить на вопрос: совместна система или нет, а если совместна, то, сколько у нее решений. Ответить на этот вопрос позволяет следующая теорема.
Теорема 6.3 (Кронекера12–Капелли13). Система линейных уравнений совместна тогда и только тогда, когда ранг основной матрицы системы равен рангу ее расширенной матрицы, то есть r(A) = r(А|B).
Для совместных систем линейных уравнений верны следующие утверждения.
Теорема 6.4. Если ранг матрицы совместной системы равен числу неизвестных, то есть r(A) = r(А|B) = n, то эта система определенная, имеет единственное решение.
Теорема 6.5. Если ранг матрицы совместной системы меньше числа неизвестных, то есть r(A) = r(А|B) < n, то система неопределенная и имеет бесконечно много решений; причем количество свободных неизвестных равно (n – r).
Пример 6.4.
Исследовать систему линейных уравнений
на совместность:
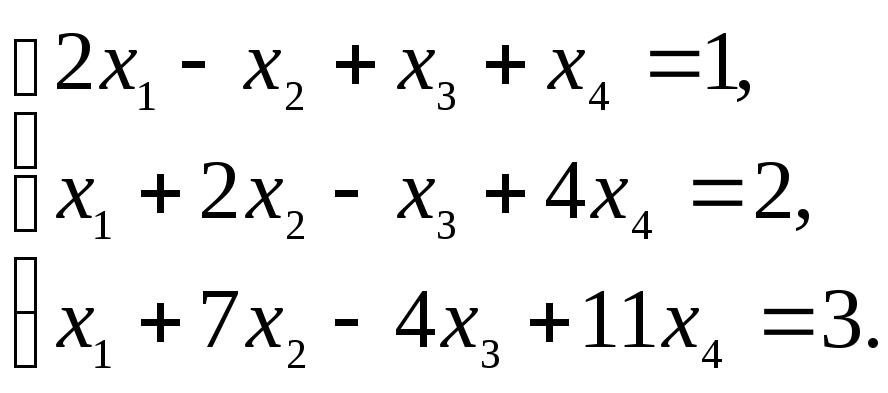
Решение. Так как в системе число уравнений меньше числа неизвестных, то применим только метод Гаусса. Приводим расширенную матрицу этой системы к ступенчатому виду с помощью элементарных преобразований.
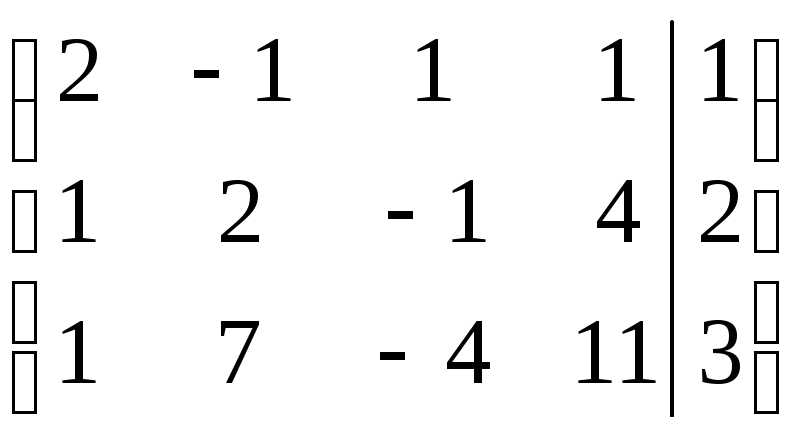
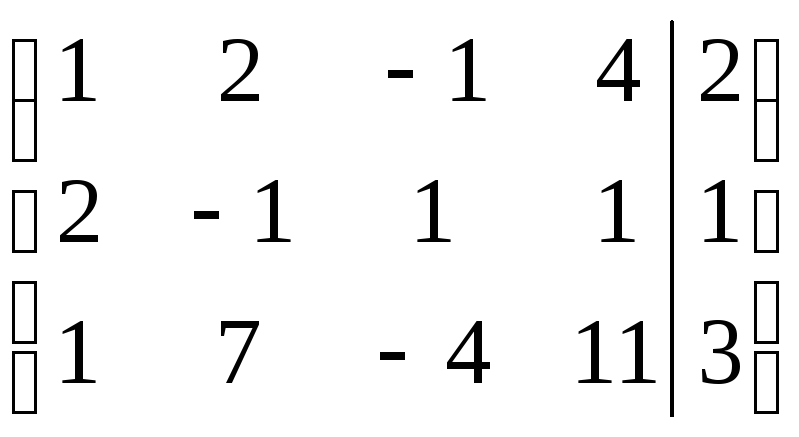

 .
.
Получили, что ранг основной матрицы равен двум, а расширенной матрицы – трем, следовательно, данная система линейных уравнений несовместна.
6.4. Однородные системы линейных уравнений
Определение 6.11. Система линейных уравнений называется однородной, если ее свободные члены равны нулю.
Однородная система m линейных уравнений с n неизвестными имеет вид:
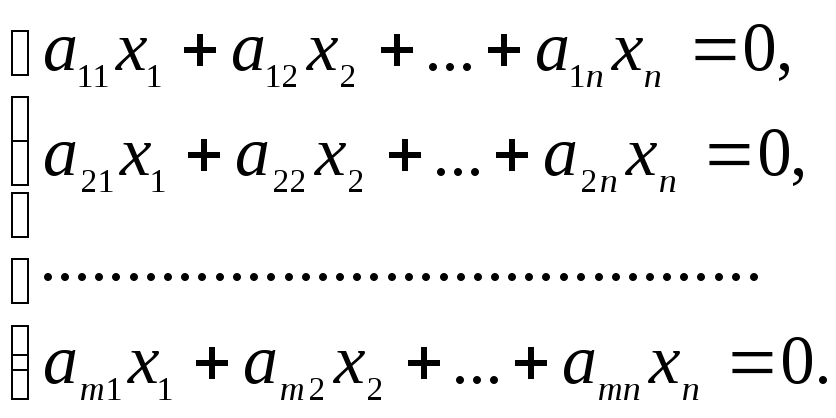 (4)
(4)
Однородная система линейных уравнений всегда совместна, так как нулевой вектор 0 = (0, 0, …, 0) является решением этой системы. Если однородная система линейных уравнений определенная (r(A) = n), то есть имеет единственное решение, то это решение нулевое (не нулевых решений нет). Если же однородная система неопределенная (r(A) < n), то кроме нулевого решения у этой системы есть ненулевые решения.
Свойства решений однородной системы линейных уравнений
Если вектор а = (1, 2, …, n) является решением однородной системы, то вектор kа = (k1, k2, …, kn) также является решением этой системы, где k – любое число.
Если векторы а = (1, 2, …, n) и b = (1, 2, …, n) являются решениями однородной системы, то вектор a + b = (1 + 1, 2 + 2, …, n + n) также является решением этой системы.
Следствие. Если а1, а2, …, аp – решения однородной системы (4), то k1а1 + k2а2 + … + kpаp – тоже решение системы (4), где k1, k2, …, kp – любые числа.
Фундаментальный набор решений однородной системы линейных уравнений
Пусть М0 – множество решений однородной системы (4) линейных уравнений.
Определение 6.12. Векторы с1, с2, …, сp, являющиеся решениями однородной системы линейных уравнений называются фундаментальным набором решений (сокращенно ФНР), если
1) векторы с1, с2, …, сp линейно независимы (т. е. ни один из них нельзя выразить через другие);
2) любое другое решение однородной системы линейных уравнений можно выразить через решения с1, с2, …, сp.
Заметим, что если с1, с2, …, сp – какой-либо ф.н.р., то выражением k1с1 + k2с2 + … + kpсp можно описать все множество М0 решений системы (4), поэтому его называют общим видом решения системы (4).
Теорема 6.6. Любая неопределенная однородная система линейных уравнений обладает фундаментальным набором решений.
Способ нахождения фундаментального набора решений состоит в следующем:
• найти общее решение однородной системы линейных уравнений;
• построить (n – r) частных решений этой системы, при этом значения свободных неизвестных должны образовывать единичную матрицу;
• выписать общий вид решения, входящего в М0.
Пример 6.5.
Найти фундаментальный набор решений
следующей системы:
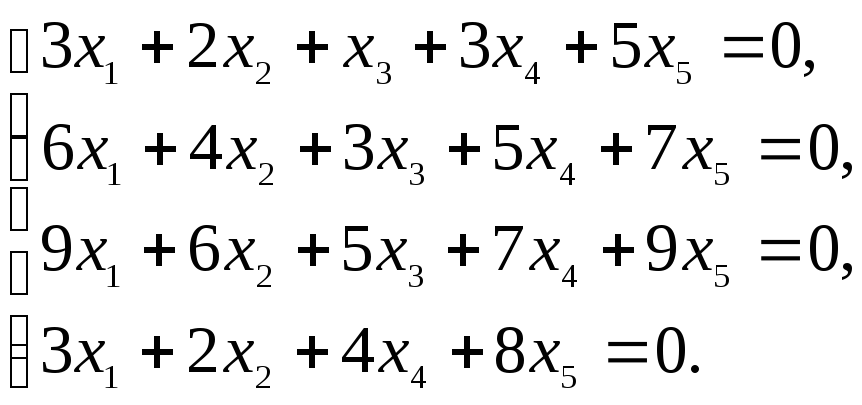
Решение. Найдем общее решение этой системы.



![]()
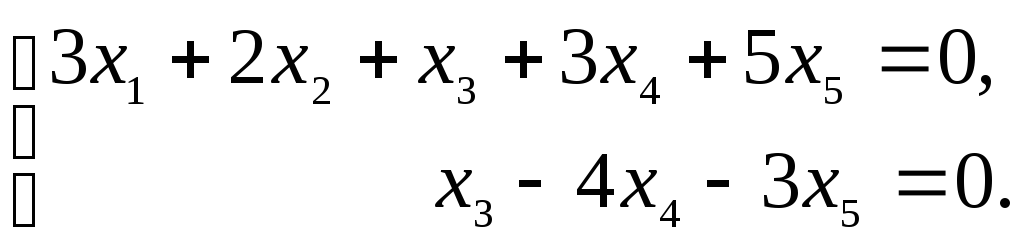
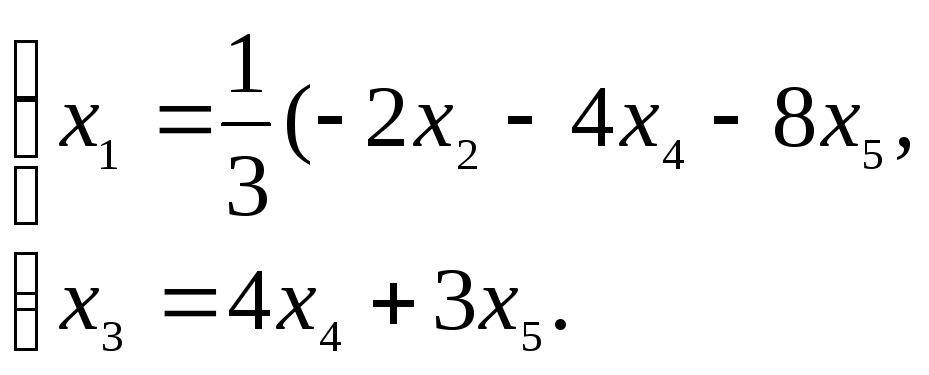 В
этой системе пять неизвестных (n = 5),
из них главных неизвестных два (r = 2),
свободных неизвестных три (n – r),
то есть в фундаментальном наборе решений
содержится три вектора решения. Построим
их.
Имеем x1
и x3
– главные неизвестные, x2,
x4,
x5
– свободные неизвестные
В
этой системе пять неизвестных (n = 5),
из них главных неизвестных два (r = 2),
свободных неизвестных три (n – r),
то есть в фундаментальном наборе решений
содержится три вектора решения. Построим
их.
Имеем x1
и x3
– главные неизвестные, x2,
x4,
x5
– свободные неизвестные
|
|
x1 |
x2 |
x3 |
x4 |
x5 |
|
с1 |
|
1 |
0 |
0 |
0 |
|
с2 |
|
0 |
1 |
1 |
0 |
|
с3 |
|
0 |
3 |
0 |
1 |
Значения свободных неизвестных x2, x4, x5 образуют единичную матрицу E третьего порядка. Получили, что векторы с1, с2, с3 образуют ф.н.р. данной системы. Тогда множество решений данной однородной системы будет М0 = {k1с1 + k2с2 + k3с3, k1, k2, k3 R}.
Выясним теперь условия существования ненулевых решений однородной системы линейных уравнений, другими словами условия существования фундаментального набора решений.
Однородная система линейных уравнений имеет ненулевые решения, то есть является неопределенной, если
ранг основной матрицы системы меньше числа неизвестных;
в однородной системе линейных уравнений число уравнений меньше числа неизвестных;
если в однородной системе линейных уравнений число уравнений равно числу неизвестных, и определитель основной матрицы равен нулю (т. е. |A| = 0).
Пример 6.6.
При каком значении параметра a
однородная система линейных уравнений
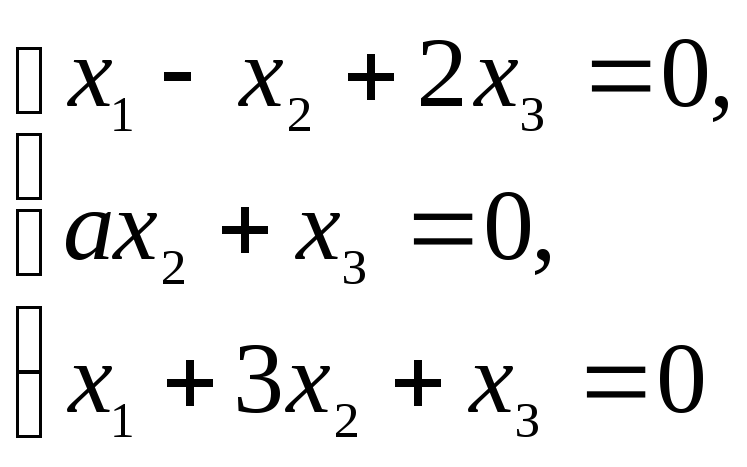 имеет ненулевые решения?
имеет ненулевые решения?
Решение.
Составим основную матрицу этой системы
и найдем ее определитель:
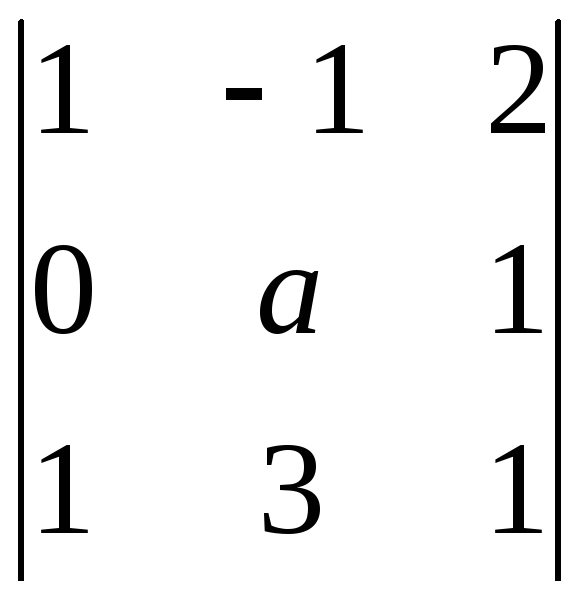 =
= 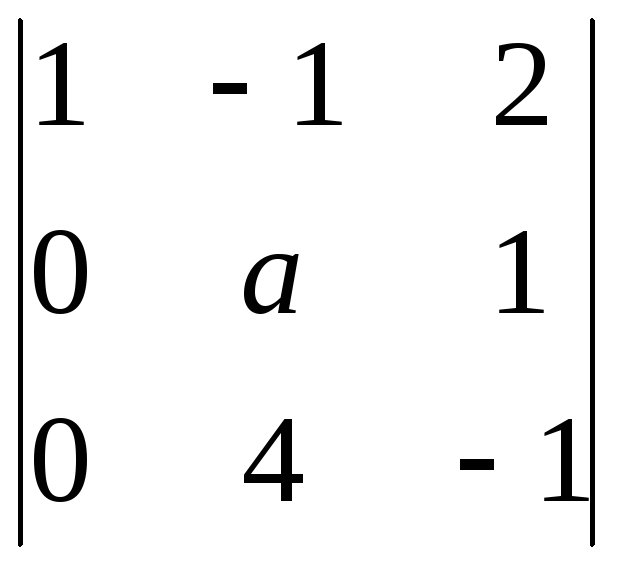 = 1(–1)1+1
= 1(–1)1+1![]() = –а – 4.
Определитель этой матрицы равен нулю
при a = –4.
= –а – 4.
Определитель этой матрицы равен нулю
при a = –4.
Ответ: –4.