ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 11.08.2024
Просмотров: 578
Скачиваний: 0
СОДЕРЖАНИЕ
Т. Н. Матыцина е. К. Коржевина линейная алгебра
1.1. Множества и их элементы. Способы задания множеств
1.2. Подмножества. Диаграммы Эйлера – Венна
1.3. Операции над множествами и их свойства
2. Пересечение (или произведение).
4. Декартовое произведение (или прямое произведение).
Свойства операций над множествами
1.4. Метод математической индукции
Операции над комплексными числами
Геометрическая интерпретация комплексных чисел
Тригонометрическая форма комплексного числа
Действия над комплексными числами в тригонометрической форме
4. Извлечение корня n-ой степени.
Показательная форма комплексного числа
Способы задания бинарных отношений
Операции над бинарными отношениями
2.2. Свойства бинарных отношений
2.3. Отношение эквивалентности
3. Матрицы и действия над ними
3.2. Основные операции над матрицами и их свойства
3.2.1. Сложение однотипных матриц
3.2.2. Умножение матрицы на число
4. Определители квадратных матриц
4.1. Определители матриц второго и третьего порядка
4.2. Определитель матрицы n-го порядка
4.4. Практическое вычисление определителей
5. Ранг матрицы. Обратная матрица
5.2. Нахождение ранга матрицы методом окаймления миноров
5.3. Нахождение ранга матрицы с помощью элементарных преобразований
5.4. Понятие обратной матрицы и способы ее нахождения
Алгоритм нахождения обратной матрицы
Нахождение обратной матрицы с помощью элементарных преобразований
6.1. Основные понятия и определения
6.2. Методы решения систем линейных уравнений
6.3. Исследование системы линейных уравнений
6.4. Однородные системы линейных уравнений
Свойства решений однородной системы линейных уравнений
Фундаментальный набор решений однородной системы линейных уравнений
7. Арифметическое n-мерное векторное пространство
7.2. Линейная зависимость и независимость системы векторов
Свойства линейной зависимости системы векторов
Две теоремы о линейной зависимости
7.3. Базис и ранг системы векторов
8. Векторные (линейные) пространства
8.1. Определение векторного пространства над произвольным полем.
Простейшие свойства векторных пространств
Линейная зависимость и независимость системы векторов
8.2. Подпространства. Линейные многообразия
Пересечение и сумма подпространств
8.3. Базис и размерность векторного пространства
8.3.1. Конечномерные векторные пространства
Базис конечномерного векторного пространства
8.3.2. Базисы и размерности подпространств
8.3.3. Координаты вектора относительно данного базиса
8.3.4. Координаты вектора в различных базисах
8.4 Евклидовы векторные пространства
Скалярное произведение в координатах
Скалярное произведение в ортонормированном базисе
Ортогональное дополнение подпространства
9.1. Основные понятия и способы задания линейных операторов
Способы задания линейных операторов
9.2. Матрица линейного оператора Связь между координатами вектора и координатами его образа
Матрицы линейного оператора в различных базисах
Свойства отношения подобия матриц
9.4. Действия над линейными операторами
1. Сложение линейных операторов.
Свойства сложения линейных операторов
9.5. Ядро и образ линейного оператора
9.6. Обратимые линейные операторы
9.7. Собственные векторы линейного оператора
9.7.1. Свойства собственных векторов
9.7.2. Характеристический многочлен матрицы
9.7.3. Нахождение собственных векторов линейного оператора
9.7.4. Алгоритм нахождения собственных векторов линейного оператора
9.7.5.Условия, при которых матрица подобна диагональной матрице
10. Жорданова нормальная форма матрицы линейного оператора
10.2. Жорданова нормальная форма
10.3.Приведение матрицы к жордановой (нормальной) форме
Алгоритм приведения матрицы a к жордановой форме
11. Билинейные и квадратичные формы
Преобразование матрицы билинейной формы при переходе к новому базису. Ранг билинейной формы
Приведение квадратичной формы к каноническому виду
Закон инерции квадратичных форм
Классификация квадратичных форм
Необходимое и достаточное условие знакоопределенности квадратичной формы
Необходимое и достаточное условие знакопеременности квадратичной формы
Необходимое и достаточное условие квазизнакопеременности квадратичной формы
5. Ранг матрицы. Обратная матрица
5.1. Понятие ранга матрицы
Пусть А – матрица размерности m n. Выберем в этой матрице произвольно k строк и k столбцов, где 1 ≤ k ≤ min(m, n).
Определение 5.1. Минором k-го порядка матрицы А называется определитель матрицы, стоящей на пересечении этих k строк и k столбцов.
Другими словами, если в матрице А размерности m n вычеркнуть (m – k) строк и (n – k) столбцов, а из оставшихся элементов составить матрицу, сохраняя расположение элементов матрицы А , то определитель полученной матрицы есть минор порядка k матрицы А.
Пример 5.1.
Проиллюстрируем определение минором
k-го
порядка матрицы А.
Рассмотрим матрицу А = 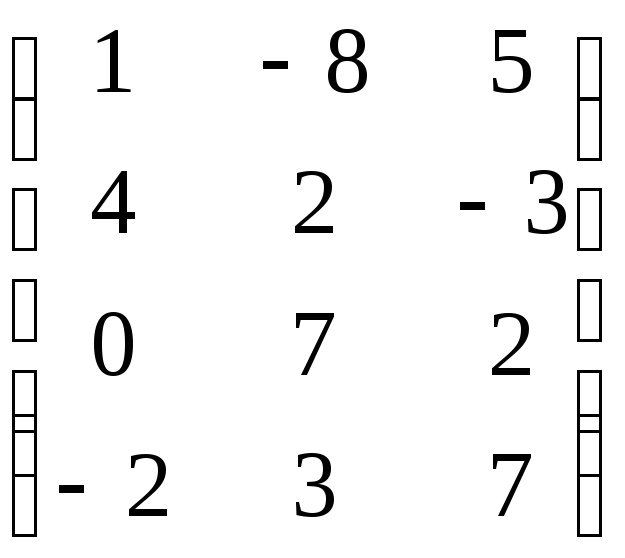 .
Запишем
минор первого порядка этой матрицы.
Например, если выбрать третью строку и
второй столбец матрицы А,
то данному выбору соответствует минор
первого порядка M1 =det(7) = 7 .
Иными словами, для получения этого
минора надо вычеркнуть первую, вторую
и четвертую строки, а также первый и
третий столбцы из матрицы А,
а из оставшегося элемента составить
определитель. Таким образом, минорами
первого порядка матрицы являются сами
элементы матрицы.
.
Запишем
минор первого порядка этой матрицы.
Например, если выбрать третью строку и
второй столбец матрицы А,
то данному выбору соответствует минор
первого порядка M1 =det(7) = 7 .
Иными словами, для получения этого
минора надо вычеркнуть первую, вторую
и четвертую строки, а также первый и
третий столбцы из матрицы А,
а из оставшегося элемента составить
определитель. Таким образом, минорами
первого порядка матрицы являются сами
элементы матрицы.
Приведем
пример минора второго порядка матрицы
А.
Выберем
две строки, например, первую и вторую,
и два столбца, например, первый и третий.
Вычислим определитель, стоящий на их
пересечении M2 = ![]() = –23.
Этот
минор также можно было составить
вычеркиванием из матрицы А
третьей
и четвертой строки, второго столбца.
= –23.
Этот
минор также можно было составить
вычеркиванием из матрицы А
третьей
и четвертой строки, второго столбца.
Аналогично
могут быть найдены миноры третьего
порядка матрицы А.
Так как в матрице А
всего
три столбца, то берем их все. Если к этим
столбцам добавить три строки, например
первую, третью и четвертую, то получим
минор третьего порядка M3 =  = 145.
Данный минор также
может быть построен вычеркиванием
второй строки матрицы А.
Можно получить другой минор третьего
порядка, если вычеркивать третью строку
матрицы А.
= 145.
Данный минор также
может быть построен вычеркиванием
второй строки матрицы А.
Можно получить другой минор третьего
порядка, если вычеркивать третью строку
матрицы А.
Для данной матрицы А миноров порядка выше третьего не существует, так как k ≤ min(m, n) = min(4, 3) = 3.
Замечание 5.1.
Число миноров
порядка k
матрицы A
размерности m n
может быть вычислено по формуле:
![]() ,
где
,
где
![]() и
и![]() – число сочетаний изm
по k
и из n по
k соответственно.
– число сочетаний изm
по k
и из n по
k соответственно.
Определение 5.2. Рангом матрицы называется наибольший из порядков ее миноров, отличных от нуля. Обозначение: rang A, r или r(A).
Из определения следует, что
для матрицы A размерности m n имеем 0 ≤ rang A ≤ min(m, n);
ранг нулевой матрицы равен нулю;
ранг ненулевой матрицы не меньше единицы;
ранг квадратной матрицы порядка n равен n только тогда, когда ее определитель не равен нулю;
ранг матрицы не меняется при транспонировании.
5.2. Нахождение ранга матрицы методом окаймления миноров
Один из методов методом нахождения ранга матрицы является метод перебора миноров. Этот способ основан на определении ранга матрицы. Суть метода в следующем. Если есть хотя бы один элемент матрицы размерности m n, отличный от нуля, то ранг матрицы как минимум равен единице (так как есть минор первого порядка, не равный нулю). Далее перебираем миноры второго порядка. Если все миноры второго порядка равны нулю, то ранг матрицы равен единице. Если существует хотя бы один ненулевой минор второго порядка, то переходим к перебору миноров третьего порядка, а ранг матрицы как минимум равен двум. Аналогично, если все миноры третьего порядка равны нулю, то ранг матрицы равен двум. Если существует хотя бы один минор третьего порядка, отличный от нуля, то ранг матрицы как минимум равен трем, и преступаем к перебору миноров четвертого порядка. И так далее.
Следует учесть, что ранг матрицы не может превышать наименьшего из чисел m и n.
Опишем более рациональный метод нахождения ранга матрицы – это метод окаймляющих миноров.
Определение 5.3. Минор М (k + 1)-ого порядка матрицы А окаймляет минор M порядка k матрицы А, если матрица, соответствующая минору М, «содержит» матрицу, соответствующую минору M.
Другими словами, матрица, соответствующая окаймляемому минору М, получается из матрицы, соответствующей окаймляющему минору M, вычеркиванием элементов одной строки и одного столбца.
Теорема 5.1. Если в матрице А имеется минор М порядка r, отличный от нуля, а все миноры матрицы А, окаймляющие минор М (если они существуют) равны нулю, то ранг матрицы А равен r.
Замечание 5.2. Данную теорему можно переформулировать иначе. Если все миноры, окаймляющие минор k-ого порядка матрицы А размерности m n, равны нулю, то все миноры порядка (k + 1) матрицы А равны нулю.
Таким образом, для нахождения ранга матрицы не обязательно перебирать все миноры, достаточно окаймляющих. Количество миноров, окаймляющих минор k-ого порядка матрицы А размерности m n, находится по формуле (m – k)(n – k). Отметим, что миноров, окаймляющих минор k-ого порядка матрицы А, не больше, чем миноров (k + 1)-ого порядка матрицы А. Поэтому, в большинстве случаев использование метода окаймляющих миноров выгоднее простого перебора всех миноров.
Опишем алгоритм данного метода.
Если матрица А ненулевая, то в качестве минора первого порядка берем любой элемент матрицы А, отличный от нуля. Рассматриваем его окаймляющие миноры. Если все они равны нулю, то ранг матрицы равен единице. Если же есть хотя бы один ненулевой окаймляющий минор (его порядок равен двум), то переходим к рассмотрению его окаймляющих миноров. Если все они равны нулю, то rang A = 2. Если хотя бы один окаймляющий минор отличен от нуля (его порядок равен трем), то рассматриваем его окаймляющие миноры. И так далее. В итоге rang A =k, если все окаймляющие миноры (k + 1)-ого порядка матрицы А равны нулю, либо rang A = min(m, n), если существует ненулевой минор, окаймляющий минор порядка (min(m, n) – 1).
Пример 5.2.
Найти
ранг матрицы A = 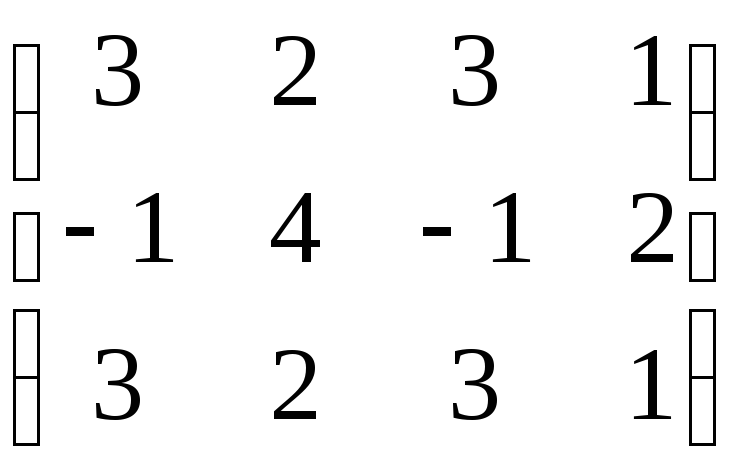 методом
окаймляющих миноров.
методом
окаймляющих миноров.
Решение.
В этой матрице есть ненулевые элементы,
значит ее ранг больше нуля. Так
как элемент а11 = 3
матрицы
А
отличен
от нуля, то возьмем его в качестве минора
первого порядка. Начнем поиск окаймляющего
минора, отличного от нуля:
![]() = 14 ≠ 0.
= 14 ≠ 0.
Находим
миноры третьего порядка, окаймляющие
данный (их
(3 – 2)(4 – 2) = 2
штуки)
 = 0,
= 0,
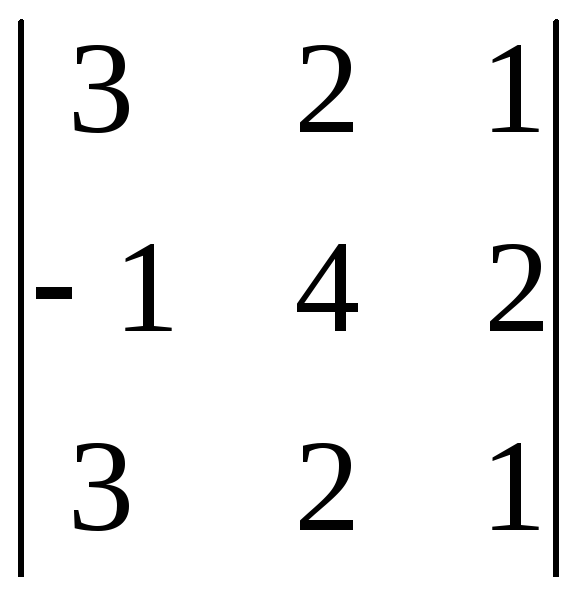 = 0.
Все
они равны нулю, следовательно ранг
матрицы А
равен двум, rang A = 2.
= 0.
Все
они равны нулю, следовательно ранг
матрицы А
равен двум, rang A = 2.
5.3. Нахождение ранга матрицы с помощью элементарных преобразований
Рассмотрим еще один способ нахождения ранга матрицы.
Определение 5.4. Элементарными преобразованиями матрицы называются следующие преобразования:
умножение строки матрицы на число, отличное от нуля;
прибавление к элементам какой-либо строки (столбца) матрицы соответствующих элементов другой строки (столбца), умноженных на произвольное число;
вычеркивание нулевой строки.
Замечание 5.3. С помощью преобразований 1 и 2 можно поменять местами любые две строки (столбца) матрицы.
Определение 5.5.
Матрица А
называется ступенчатой,
если она имеет вид:
 ,
aii
≠ 0,
i = 1,
2, …, r,
r k.
,
aii
≠ 0,
i = 1,
2, …, r,
r k.
Замечание 5.4. Условие r k всегда может быть достигнуто транспонированием матрицы.
Теорема 5.2. Применение к произвольной матрице цепочки элементарных преобразований не меняет ее ранга.
Теорема 5.3. Любую матрицу с помощью элементарных преобразований можно привести к ступенчатому виду.
Теорема 5.4. Ранг ступенчатой матрицы равен количеству ее ненулевых строк.
Определение 5.6. Первый ненулевой элемент строки называется ее ведущим элементом.
Из этих теорем следует практический способ нахождения ранга матрицы: с помощью элементарных преобразований привести матрицу к ступенчатому виду и определить количество ее ненулевых строк.·
Пример 5.3.
Найти ранг матрицы А =  с помощью элементарных преобразований.
с помощью элементарных преобразований.
Решение.
Приводим
матрицу с помощью элементарных
преобразований к ступенчатому виду.
Выберем в 1-ой строке ведущий элемент.
Это (–1). В столбце под этим элементом
следует получить нули. Для этого к 2-ой
строке прибавим 1-ю, умноженную на 2, а к
3-ей строке прибавим 1-ую, умноженную на
3; получим матрицу:
 .
Выбираем
ведущий элемент во второй строке и
получим нули в столбце под ним: к 3-ей
строке прибавим 2-ую, умноженную на (–2),
в результате получим следующую матрицу:
.
Выбираем
ведущий элемент во второй строке и
получим нули в столбце под ним: к 3-ей
строке прибавим 2-ую, умноженную на (–2),
в результате получим следующую матрицу:
 .
Получена
матрица ступенчатого вида, в которой
две ненулевые строки, следовательно,
ранг исходной равен 2, т. е. rang A = 2.
.
Получена
матрица ступенчатого вида, в которой
две ненулевые строки, следовательно,
ранг исходной равен 2, т. е. rang A = 2.