ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 11.08.2024
Просмотров: 590
Скачиваний: 0
СОДЕРЖАНИЕ
Т. Н. Матыцина е. К. Коржевина линейная алгебра
1.1. Множества и их элементы. Способы задания множеств
1.2. Подмножества. Диаграммы Эйлера – Венна
1.3. Операции над множествами и их свойства
2. Пересечение (или произведение).
4. Декартовое произведение (или прямое произведение).
Свойства операций над множествами
1.4. Метод математической индукции
Операции над комплексными числами
Геометрическая интерпретация комплексных чисел
Тригонометрическая форма комплексного числа
Действия над комплексными числами в тригонометрической форме
4. Извлечение корня n-ой степени.
Показательная форма комплексного числа
Способы задания бинарных отношений
Операции над бинарными отношениями
2.2. Свойства бинарных отношений
2.3. Отношение эквивалентности
3. Матрицы и действия над ними
3.2. Основные операции над матрицами и их свойства
3.2.1. Сложение однотипных матриц
3.2.2. Умножение матрицы на число
4. Определители квадратных матриц
4.1. Определители матриц второго и третьего порядка
4.2. Определитель матрицы n-го порядка
4.4. Практическое вычисление определителей
5. Ранг матрицы. Обратная матрица
5.2. Нахождение ранга матрицы методом окаймления миноров
5.3. Нахождение ранга матрицы с помощью элементарных преобразований
5.4. Понятие обратной матрицы и способы ее нахождения
Алгоритм нахождения обратной матрицы
Нахождение обратной матрицы с помощью элементарных преобразований
6.1. Основные понятия и определения
6.2. Методы решения систем линейных уравнений
6.3. Исследование системы линейных уравнений
6.4. Однородные системы линейных уравнений
Свойства решений однородной системы линейных уравнений
Фундаментальный набор решений однородной системы линейных уравнений
7. Арифметическое n-мерное векторное пространство
7.2. Линейная зависимость и независимость системы векторов
Свойства линейной зависимости системы векторов
Две теоремы о линейной зависимости
7.3. Базис и ранг системы векторов
8. Векторные (линейные) пространства
8.1. Определение векторного пространства над произвольным полем.
Простейшие свойства векторных пространств
Линейная зависимость и независимость системы векторов
8.2. Подпространства. Линейные многообразия
Пересечение и сумма подпространств
8.3. Базис и размерность векторного пространства
8.3.1. Конечномерные векторные пространства
Базис конечномерного векторного пространства
8.3.2. Базисы и размерности подпространств
8.3.3. Координаты вектора относительно данного базиса
8.3.4. Координаты вектора в различных базисах
8.4 Евклидовы векторные пространства
Скалярное произведение в координатах
Скалярное произведение в ортонормированном базисе
Ортогональное дополнение подпространства
9.1. Основные понятия и способы задания линейных операторов
Способы задания линейных операторов
9.2. Матрица линейного оператора Связь между координатами вектора и координатами его образа
Матрицы линейного оператора в различных базисах
Свойства отношения подобия матриц
9.4. Действия над линейными операторами
1. Сложение линейных операторов.
Свойства сложения линейных операторов
9.5. Ядро и образ линейного оператора
9.6. Обратимые линейные операторы
9.7. Собственные векторы линейного оператора
9.7.1. Свойства собственных векторов
9.7.2. Характеристический многочлен матрицы
9.7.3. Нахождение собственных векторов линейного оператора
9.7.4. Алгоритм нахождения собственных векторов линейного оператора
9.7.5.Условия, при которых матрица подобна диагональной матрице
10. Жорданова нормальная форма матрицы линейного оператора
10.2. Жорданова нормальная форма
10.3.Приведение матрицы к жордановой (нормальной) форме
Алгоритм приведения матрицы a к жордановой форме
11. Билинейные и квадратичные формы
Преобразование матрицы билинейной формы при переходе к новому базису. Ранг билинейной формы
Приведение квадратичной формы к каноническому виду
Закон инерции квадратичных форм
Классификация квадратичных форм
Необходимое и достаточное условие знакоопределенности квадратичной формы
Необходимое и достаточное условие знакопеременности квадратичной формы
Необходимое и достаточное условие квазизнакопеременности квадратичной формы
5.4. Понятие обратной матрицы и способы ее нахождения
Пусть дана квадратная матрица А.
Определение 5.7. Матрица А–1 называется обратной для матрицы А, если АА–1 = А–1А = Е.
Определение 5.8. Квадратная матрица А называется невырожденной, если ее определитель не равен нулю.
Заметит, что ранг невырожденной матрицы порядка n равен n.
Определение 5.9. Квадратная матрица А называется вырожденной, если ее определитель равен нулю.
Определение 5.10.
Матрицей, присоединенной
к матрице А,
называется матрица А*,
где А* = 
,
Аij
– алгебраическое
дополнение элемента аij
для всех индексов i,
j = 1,
2, …n.
Теорема 5.5. Для вырожденной матрицы не существует обратной матрицы.
Теорема 5.6.
Для невырожденной матрицы А
существует обратная матрица, причем
только одна. Обратная матрица может
быть найдена по формуле: А–1 = 
А*.
Алгоритм нахождения обратной матрицы
Рассмотрим один из способов нахождения обратной матрицы к данной с помощью алгебраических дополнений. Пусть дана квадратная матрица А.
Находим определитель матрицы |A|. Если |A| = 0, то у матрицы А нет обратной (теорема 5.5). Если |A| ≠ 0, то обратная матрица существует, и переходим к пункту 2.
Находим алгебраические дополнения всех элементов матрицы А.
Составляем присоединенную матрицу А*.
Находим А–1 по указанной формуле (теорема 5.6).
Пример 5.4.
Найти матрицу, обратную для матрицы
А = 
.
Решение.
Определитель
матрицы А
равен 1, то есть не равен нулю. Тогда
находим алгебраические дополнения
элементов матрицы. А11 = 3,
А21 = –5,
А12 = –1,
А22 = 2.
Составляем присоединенную матрицу А*,
получаем А* = 
.
С учетом формулы А–1 = 
А*
находим обратную матрицу А–1,
А–1 = 
= 
.
Нахождение обратной матрицы с помощью элементарных преобразований
Рассмотрим еще способ нахождения обратной матицы с помощью элементарных преобразований. Сформулируем необходимые понятия и теоремы.
Определение 5.11. Матрица В называется эквивалентной матрице А, если В получена из А с помощью конечного числа элементарных преобразований. Обозначение В А.
Теорема 5.7. Всякую невырожденную квадратную матрицу с помощью элементарных преобразований можно привести к единичной матрице.
Теорема 5.8. Если к единичной матрице применить те же самые элементарные преобразования, которые матрицу А переводят в единичную, то полученная матрица будет обратной для матрицы А.
Схематично преобразования выглядят так: (А|E) … (Е|А–1).
Замечание 5.5. При нахождении матрицы А–1 нет необходимости проверять невырожденность матрицы А, т. к. сама возможность привести матрицу А к единичной матрице Е будет означать, что А – невырожденная.
Пример 5.5.
Найти матрицу, обратную для матрицы
А = 
с помощью элементарных преобразований.
Решение. Приписываем к матрице А (справа, а можно и слева) единичную матрицу Е. Далее, с помощью элементарных преобразований над всей составной матрицей приводим матрицу А к единичной Е. Тогда на месте первоначально приписанной матрицы Е оказывается матрица А–1.
;
т. о. А–1 = 
.
6. Системы линейных уравнений
6.1. Основные понятия и определения
Определение 6.1. Системой m линейных уравнений с n неизвестными называется система вида:
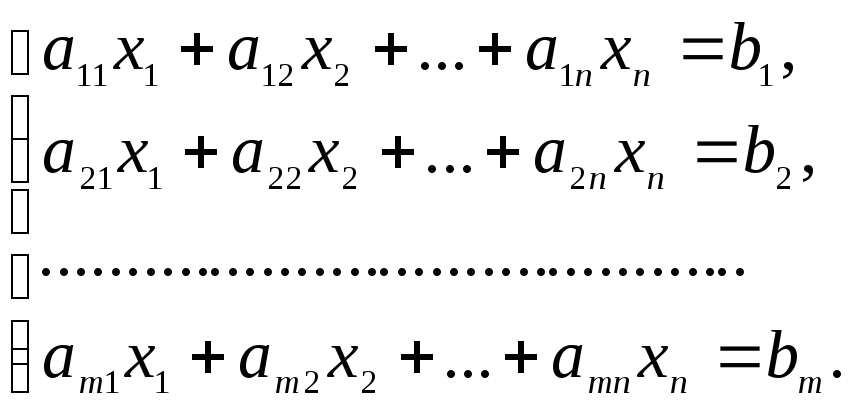(1)
Здесь x1, …, xn – неизвестные (или переменные), числа аij – коэффициенты при неизвестных, i – номер уравнения, j – номер неизвестного, b1, …, bm – свободные члены.
Короче
систему (1) можно записать в виде:
,
где i = 1,
2, …, m.
С каждой системой вида (1) связаны следующие матрицы: А – основная матрица системы, составленная из коэффициентов при неизвестных; В – матрица-столбец свободных членов, Х – матрица-столбец неизвестных; (А|B) – расширенная матрица системы.
Аmn =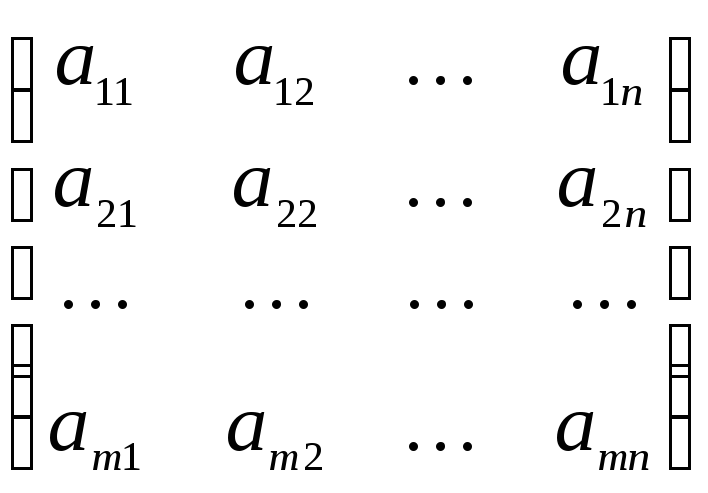 
,
Bm1 = 
,
Xn1 = 
,
(А|B)m(n + 1) =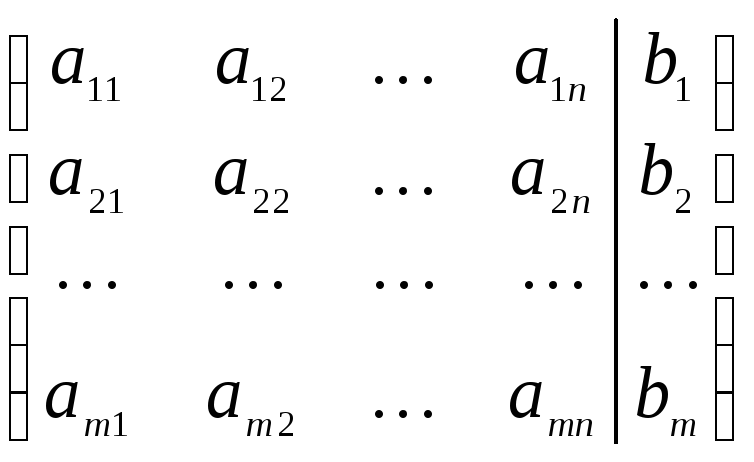 
.
Из определения 6.1 видно, что матрицы А и Х согласованы, следовательно можно найти их произведение:
АХ =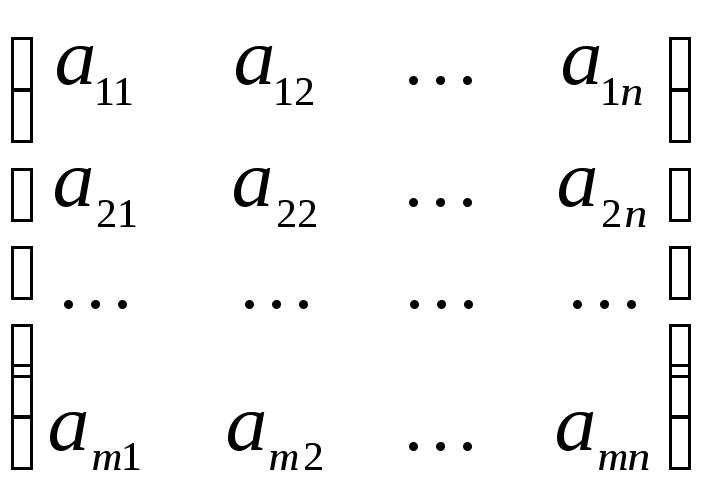 
= 
.
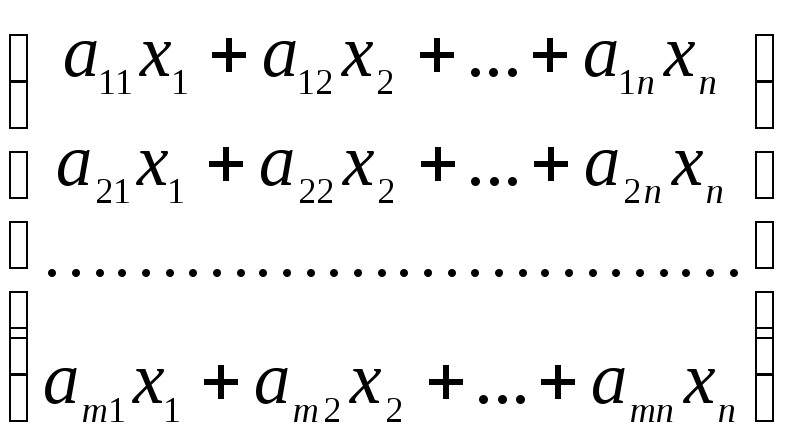Если воспользоваться определением 3.4 равенства матриц, то равенство
АХ = В (2)
записывается в виде системы линейных уравнений (1).
Определение 6.2. Уравнение (2) называют матричной формой записи системы (1).
Определение 6.3. Решением системы линейных уравнений (1) называется любой упорядоченный набор (кортеж, вектор) а = (1, 2, …, n) из чисел, который при подстановке в систему каждое уравнение обращает в верное равенство.
Таким образом, если а = (1, 2, …, n) решение системы, то следующие равенства верны:
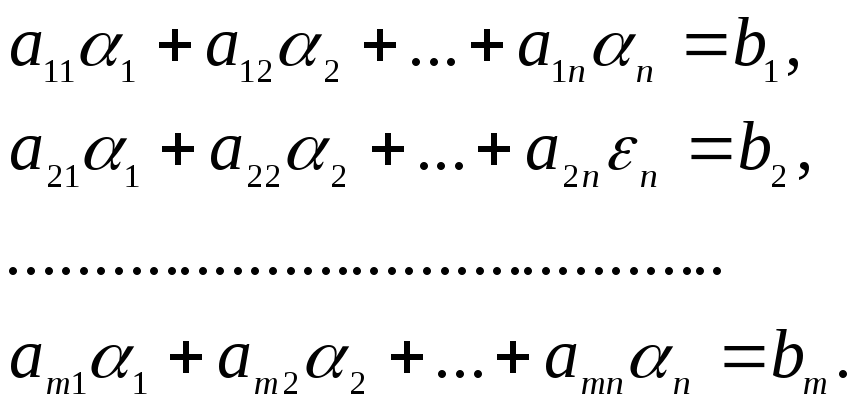
Определение 6.4. Система линейных уравнений называется совместной, если она имеет хотя бы одно решение, и несовместной, если она не имеет ни одного решения.
Определение 6.5. Система линейных уравнений называется определенной, если она имеет единственное решение, и неопределенной, если она имеет более одного решения.
Определение 6.6. Две системы линейных уравнений называются равносильными, если множества их решений совпадают.
То есть, если упорядоченный набор чисел а = (1, 2, …, n) является решением первой системы, то он является решением второй и наоборот, если упорядоченный набор чисел является решением второй системы, то он является решением первой системы.