ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 11.08.2024
Просмотров: 586
Скачиваний: 0
СОДЕРЖАНИЕ
Т. Н. Матыцина е. К. Коржевина линейная алгебра
1.1. Множества и их элементы. Способы задания множеств
1.2. Подмножества. Диаграммы Эйлера – Венна
1.3. Операции над множествами и их свойства
2. Пересечение (или произведение).
4. Декартовое произведение (или прямое произведение).
Свойства операций над множествами
1.4. Метод математической индукции
Операции над комплексными числами
Геометрическая интерпретация комплексных чисел
Тригонометрическая форма комплексного числа
Действия над комплексными числами в тригонометрической форме
4. Извлечение корня n-ой степени.
Показательная форма комплексного числа
Способы задания бинарных отношений
Операции над бинарными отношениями
2.2. Свойства бинарных отношений
2.3. Отношение эквивалентности
3. Матрицы и действия над ними
3.2. Основные операции над матрицами и их свойства
3.2.1. Сложение однотипных матриц
3.2.2. Умножение матрицы на число
4. Определители квадратных матриц
4.1. Определители матриц второго и третьего порядка
4.2. Определитель матрицы n-го порядка
4.4. Практическое вычисление определителей
5. Ранг матрицы. Обратная матрица
5.2. Нахождение ранга матрицы методом окаймления миноров
5.3. Нахождение ранга матрицы с помощью элементарных преобразований
5.4. Понятие обратной матрицы и способы ее нахождения
Алгоритм нахождения обратной матрицы
Нахождение обратной матрицы с помощью элементарных преобразований
6.1. Основные понятия и определения
6.2. Методы решения систем линейных уравнений
6.3. Исследование системы линейных уравнений
6.4. Однородные системы линейных уравнений
Свойства решений однородной системы линейных уравнений
Фундаментальный набор решений однородной системы линейных уравнений
7. Арифметическое n-мерное векторное пространство
7.2. Линейная зависимость и независимость системы векторов
Свойства линейной зависимости системы векторов
Две теоремы о линейной зависимости
7.3. Базис и ранг системы векторов
8. Векторные (линейные) пространства
8.1. Определение векторного пространства над произвольным полем.
Простейшие свойства векторных пространств
Линейная зависимость и независимость системы векторов
8.2. Подпространства. Линейные многообразия
Пересечение и сумма подпространств
8.3. Базис и размерность векторного пространства
8.3.1. Конечномерные векторные пространства
Базис конечномерного векторного пространства
8.3.2. Базисы и размерности подпространств
8.3.3. Координаты вектора относительно данного базиса
8.3.4. Координаты вектора в различных базисах
8.4 Евклидовы векторные пространства
Скалярное произведение в координатах
Скалярное произведение в ортонормированном базисе
Ортогональное дополнение подпространства
9.1. Основные понятия и способы задания линейных операторов
Способы задания линейных операторов
9.2. Матрица линейного оператора Связь между координатами вектора и координатами его образа
Матрицы линейного оператора в различных базисах
Свойства отношения подобия матриц
9.4. Действия над линейными операторами
1. Сложение линейных операторов.
Свойства сложения линейных операторов
9.5. Ядро и образ линейного оператора
9.6. Обратимые линейные операторы
9.7. Собственные векторы линейного оператора
9.7.1. Свойства собственных векторов
9.7.2. Характеристический многочлен матрицы
9.7.3. Нахождение собственных векторов линейного оператора
9.7.4. Алгоритм нахождения собственных векторов линейного оператора
9.7.5.Условия, при которых матрица подобна диагональной матрице
10. Жорданова нормальная форма матрицы линейного оператора
10.2. Жорданова нормальная форма
10.3.Приведение матрицы к жордановой (нормальной) форме
Алгоритм приведения матрицы a к жордановой форме
11. Билинейные и квадратичные формы
Преобразование матрицы билинейной формы при переходе к новому базису. Ранг билинейной формы
Приведение квадратичной формы к каноническому виду
Закон инерции квадратичных форм
Классификация квадратичных форм
Необходимое и достаточное условие знакоопределенности квадратичной формы
Необходимое и достаточное условие знакопеременности квадратичной формы
Необходимое и достаточное условие квазизнакопеременности квадратичной формы
Множество М решений общей системы m линейных уравнений с n неизвестными так же является подмножеством множества Rn и равно сумме множества М0 и вектора а, где а – некоторое частное решение исходной системы, а множество М0 – множество решений однородной системы линейных уравнений, сопутствующей данной системе (она отличается от исходной только свободными членами),
М = а + М0 = {а = m, m М0}.
Это означает, что множество М является линейным многообразием пространства Rn с вектором сдвига а и направлением М0.
Пример 8.6.
Найти базис и размерность подпространства,
заданного однородной системой линейных
уравнений:
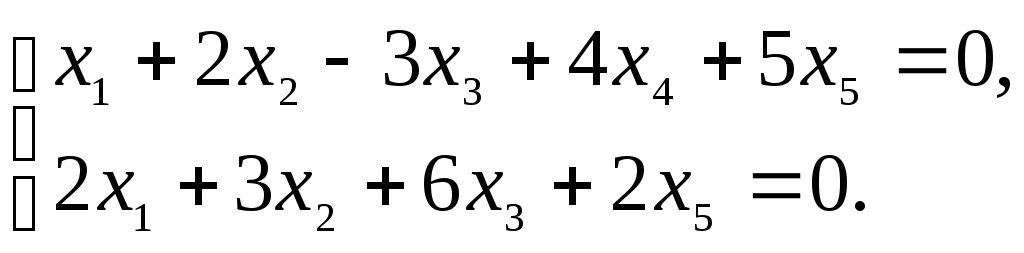
Решение.
Найдем общее решение этой системы и ее
фундаментальный набор решений:
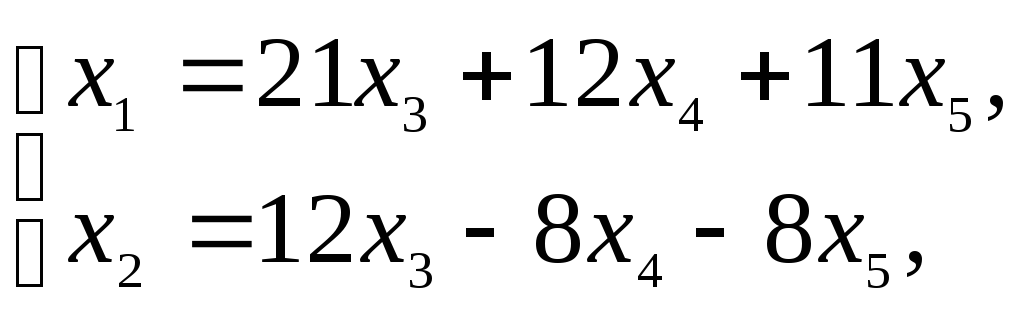с1 = (–21,
12, 1, 0, 0), с2 = (12,
–8, 0, 1, 0), с3 = (11,
–8, 0, 0, 1).
Базис подпространства образуют векторы с1, с2, с3, его размерность равна трем.
8.3.3. Координаты вектора относительно данного базиса
Рассмотрим конечномерное векторное пространство V размерности n, векторы e1, e2, …, en образуют его базис. Пусть a – произвольный вектор пространства V, тогда вектор линейно выражается через векторы базиса, a = 1e1 + 2e2 + … + nen.
Теорема 8.8. Разложение вектора a по векторам базиса производится единственным образом.
Доказательство. Предположим, что вектор a можно разложить по векторам базиса двумя способами:
a = 1e1 + 2e2 + … + nen.
a = '1e1 + '2e2 + … + 'nen.
После вычитания из одного равенства другого, получим
(1 – '1) e1 + (2 – '2)e2 + … + (n – 'n)en = 0,
из чего в силу линейной независимости базисных векторов e1, e2, …, en следует, что 1 – '1 = 0, 2 – '2 = 0, …, n – 'n = 0, а затем что 1 = '1, 2 = '2, …, n = 'n. Таким образом, коэффициенты разложения определяются однозначно. Теорема доказана.
Определение 8.13. Координатами вектора a относительно базиса e1, e2, …, en называются коэффициенты разложения вектора a по базисным векторам.
Координаты
вектора принято записывать или в виде
строки координат (координатной строки)
– (1, 2, …, n),
или в виде координатного столбца:
[a] = 
.
Пример 8.7.
1) В
пространстве R22
вектор A = 
раскладывается
по векторам базиса Е1,
Е2,
Е3,
Е4
следующим образом: А = 2Е1 – Е2 + 4Е3 + 7Е4,
следовательно, координатная строка
этого вектора равна (2, –1, 4, 7).
2) В
пространстве выбран базис
а1 = (1,
3, –1), а2 = (–2,
1, 1),
а3 = (2,
–2, –1). Найти координаты вектора a = (3,
0, –2) относительно базиса а1,
а2,
а3.
Векторное равенство a = x1а1 + x2а2 + x3а3
перепишем в виде системы линейных
уравнений
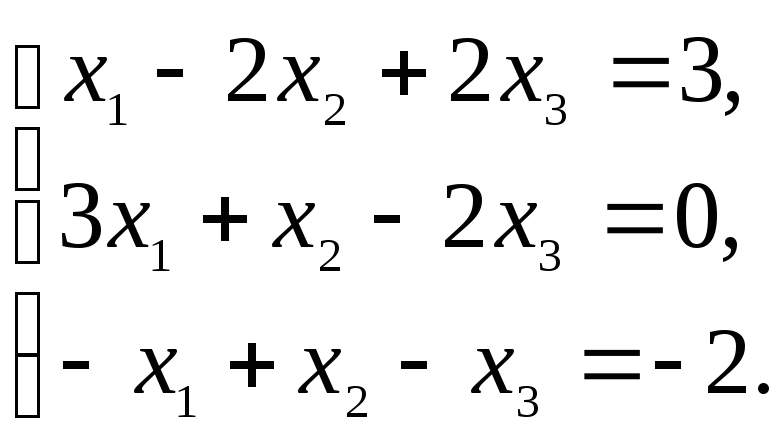Решая
эту систему, получим x1 = 1,
x2 = 1,
x3 = 2,
следовательно, координатная строка
вектора a
равна (1, 1, 2).
Каждому вектору a из произвольного векторного пространства V, в котором задан базис e1, e2, …, en, сопоставляется строка (или столбец) координат (1, 2, …, n), причем единственным образом. Если V пространство размерности n, то строка координат принадлежит пространству Rn, то есть возникает отображение: V Rn. Обратно, по строке координат (1, 2, …, n), (по вектору из Rn) единственным образом можно построить вектор a = 1e1 + 2e2+ … + nen. Для этого отображения верна следующая теорема.
Теорема 8.9. Если векторы а1, а2, …, аm из произвольного пространства V образуют линейно независимую систему векторов, то их строки (или столбцы) координат тоже линейно независимы.
8.3.4. Координаты вектора в различных базисах
Пусть V – n-мерное векторное пространство, в котором заданы два базиса: e1, e2, …, en – старый базис, e'1, e'2, …, e'n – новый базис. У произвольного вектора a есть координаты в каждом из них:
a = 1e1 + 2e2+ … + nen;
a = '1e'1 + '2e'2+ … + 'ne'n.
Для того чтобы установить связь между столбцами координат вектора a в старом и новом базисах, надо разложить векторы нового базиса по векторам старого базиса:
e'1 = 11e1 + 21e2+ … + n1en,
e'2 = 12e1 + 22e2+ … + n2en,
………………………………..
e'n = 1ne1 + 2ne2+ … + nnen.
Определение 8.14. Матрицей перехода от старого базиса к новому базису называется матрица, составленная из координат векторов нового базиса относительно старого базиса, записанных в столбцы, т. е.
T =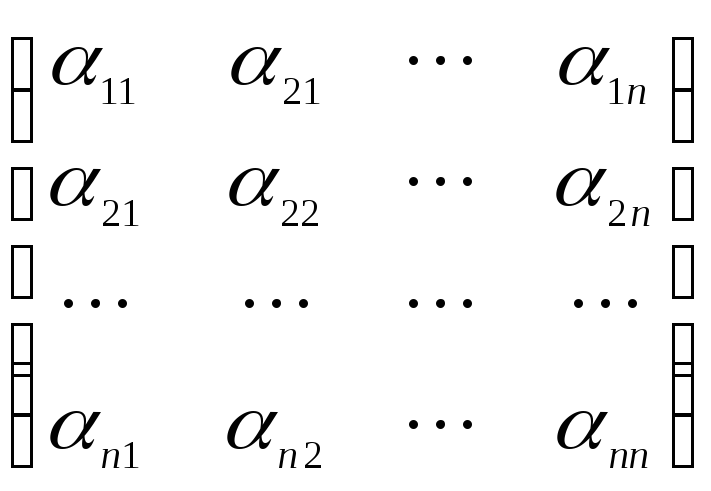 
.
Столбцы матрицы T – это координаты базисных, а значит, линейно независимых, векторов, следовательно, эти столбцы линейно независимы. Матрица с линейно независимыми столбцами является невырожденной, ее определитель не равен нулю и для матрицы T существует обратная матрица T –1.
Обозначим столбцы координат вектора a в старом и новом базисах, соответственно, как [a] и [a]'. С помощью матрицы перехода устанавливается связь между [a] и [a]'.
Теорема 8.10. Столбец координат вектора a в старом базисе равен произведению матрицы перехода на столбец координат вектора a в новом базисе, то есть [a] = T [a]'.
Следствие. Столбец координат вектора a в новом базисе равен произведению матрицы, обратной матрице перехода, на столбец координат вектора a в старом базисе, то есть [a]' = T –1[a].
Пример 8.8. Составить матрицу перехода от базиса e1, e2, к базису e'1, e'2, где e'1 = 3e1 + e2, e'2 = 5e1 + 2e2, и найти координаты вектора a = 2e'1 – 4e'2 в старом базисе.
Решение.
Координатами новых базисных векторов
относительно старого базиса являются
строки (3, 1) и (5, 2), тогда матрица
T
примет вид
.
Так как [a]' = 
,
то [a] = 
= 
.
Пример 8.9. Даны два базиса e1, e2 – старый базис, e'1, e'2 – новый базис, причем e'1 = 3e1 + e2, e'2 = 5e1 + 2e2. Найти координаты вектора a = 2e1 – e2 в новом базисе.
Решение.
1 способ.
По условию даны координаты вектора а
в старом базисе: [a] = 
.
Найдем
матрицу перехода от старого базиса e1,
e2
к новому базису e'1,
e'2.
Получим матрицу Т = 
для нее найдем обратную матрицу T –1 = 
.
Тогда согласно следствию из теоремы 8.10
имеем [a]' = T –1[a] = 
= 
.
2 способ. Так как e'1, e'2 базис, то вектор а раскладывается по базисным векторам следующим образом a = k1e'1 – k2e'2. Найдем числа k1 и k2 – это и будут координаты вектора а в новом базисе.
a = k1e'1 – k2e'2 = k1(3e1 + e2) – k2(5e1 + 2e2) =
= e1(3k1 + 5k2) + e2(k1 + 2k2) = 2e1 – e2.
Так
как координаты одного и того же вектора
в данном базисе определяется однозначно,
то имеем систему:
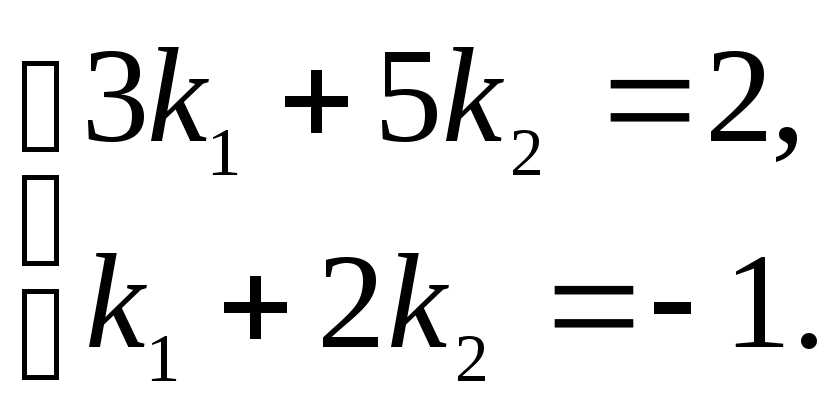Решая данную систему, получим k1 = 9
и k2 = –5,
т. о. [a]' = 
.