ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 23.08.2024
Просмотров: 2257
Скачиваний: 1
СОДЕРЖАНИЕ
Основные понятия и законы химии Атомно - молекулярное учение.
Закон сохранения массы веществ
Составление химических уравнений
Расчеты по химическим уравнениям
Закон Авогадро и молярный объем газа
Основные классы неорганических
2. Разложение некоторых кислородсодержащих веществ (оснований, кислот, солей) при нагревании:
Графическое изображение формул
Химическое равновесие. Константа химического равновесия
Энергия Гиббса направленность химических процессов
Примеры термодинамических расчетов
Химическая кинетика. Скорость химической реакции
Молекулярность элементарных реакций
Смещение химического равновесия
3 Влияние температуры на положение равновесия
Основные характеристики растворов
Растворимость газов в жидкостях
Взаимная растворимость жидкостей
Растворимость твердых веществ в жидкостях
1. Давление насыщенного пара разбавленных растворов
2. Давление пара идеальных и реальных растворов
3. Температура кристаллизации разбавленных растворов
4. Температура кипения разбавленных растворов
5. Осмотическое давление разбавленных растворов
6. Понятие активности растворенного вещества
Слабые электролиты. Константа диссоциации
Количественные характеристики процесса гидролиза соли.
Направленность реакций в растворах электролитов
Протонная теория Брёнстеда-Лоури
Коррозия металлов и методы защиты металлов от коррозии
Волновое уравнение. Квантовомеханическое объяснение строения атома
Электронная структура атомов и периодическая система элементов
Структура периодической системы элементов д.И. Менделеева.
Периодичность свойств химических элементов и их соединений
Ковалентная связь. Метод валентных связей
Способы образования ковалентной связи
Гибридизация атомных орбиталей
Квантовомеханические теории строения комплексных соединений
2. Гибридизация орбиталей и структура комплексов
Строение атома
Большую роль в установлении структуры атома сыграло открытие и изучение радиоактивности. Кроме того, на рубеже XIX–XX вв. были открыты такие явления, как фотоэлектрический эффект, катодные лучи, рентгеновские лучи. Эти открытия свидетельствовали о сложной структуре атома.
Первоначально были предложены две модели атома. Согласно модели Томсона, атом состоит из положительного заряда, равномерно распределенного по всему объему атома, и электронов, колеблющихся внутри этого заряда. Для проверки гипотезы Томсона Резерфорд провел опыты по рассеиванию α -частиц металлическими пластинками. Эти опыты показали, что основная доля α-частиц проходила через пластинки беспрепятственно, т.е. подавляющая часть пространства, занимаемого атомом, является “пустой”, а почти вся его масса занимает очень малую долю объема. Резерфордом в 1911 г. была предложена планетарная модель атома. Согласно этой модели, атом состоит из положительно заряженного ядра, в котором сосредоточена преобладающая часть массы атома, и вращающихся вокруг него электронов.
Эта модель первоначально не могла объяснить устойчивость атома, т.к. вращающийся вокруг ядра электрон должен излучать энергию. Любая заряженная частица, движущаяся с ускорением, излучает электромагнитные волны. Движение электрона вокруг ядра является ускоренным (центростремительное ускорение) и в конце концов “упасть” на ядро. Вторым противоречием этой модели была невозможность объяснить линейчатый характер атомных спектров, т.е. излучение атомом электромагнитных волн только с определенными длинами волн.
Для устранения этих противоречий Бор в 1913 г. дополнил планетарную модель атома на основе следующих предположений (постулаты Бора):
1) Электрон может вращаться вокруг ядра не по любым орбитам, а лишь по некоторым определенным (стационарным) орбитам, на которых он не излучает энергии.
2) Ближайшая к ядру орбита соответствует наиболее устойчивому состоянию атома. При сообщении энергии извне электрон может перейти на одну из более удаленных орбит (возбужденное состояние атома).
3) Поглощение и излучение энергии атомом может происходить только при переходе электрона с одной орбиты на другую. При этом разность энергий начального и конечного состояний воспринимается или отдается в виде кванта лучистой энергии. Этому излучению соответствует частота колебаний ν, выражаемая уравнением Планка:
h = Eн – Eк,
где h – постоянная Планка (h=6,6210–34 Джс); Ен, Ек – соответственно энергии начального и конечного состояний.
Обратимся к экспериментальным фактам. При нагревании в водородной лампе электрон атома водорода в результате "накачки" энергией скачком переходит на на более удаленные от ядра уровни. Но возбужденное состояние атома неустойчиво, поэтому неизбежно происходит обратный процесс - "падение" электрона на более близкие к ядру уровни (рис.1). Каждое такое падение должно сопровождаться выделением определенной порции световой энергии, соответствующей разнице энергий между уровнями. Эти конечные порции энергии называются квантами. Например, переход электрона с одного из высоких уровней на 2-й уровень сопровождается выделением определенной порции световой энергии - кванта синего света. Переход между близко расположенными уровнями дает менее энергичный квант красного цвета. Наиболее энергичные (ультрафиолетовые) кванты выделяются при возврате электрона на ближайший к ядру 1-й уровень. Кванты одного вида сливаются вместе и наблюдаются в спектрометре в виде тонких линий. По числу линий в спектре можно судить о количестве электронных уровней в атоме водорода.
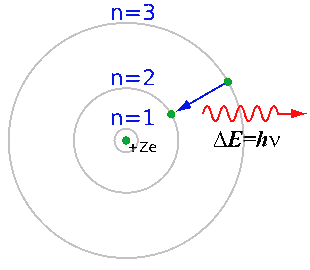
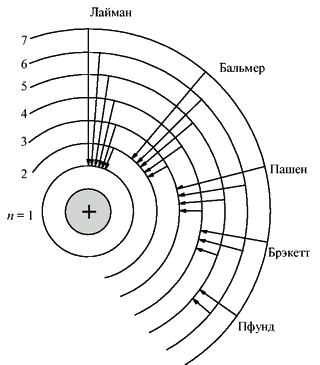
Рис. 1 Электронные подуровни атома, объясняющие происхождение в спектрах "резких" (sharp), "главных" (principle) и "размытых" (diffuse) линий.
Исходя из этих представлений, были вычислены радиусы стационарных орбит. Они относятся друг к другу как квадраты натуральных чисел 12:22:32::n2. Величина n (порядковый номер орбиты, или номер энергетического уровня) была названа главным квантовым числом. Для атома водорода радиус ближайшей к ядру орбиты равен 52,9 10–12 м. Электрон вращается по ней со скоростью 2200 км/ч.
Максимально возможное число электронов на каждом уровне равно удвоенному квадрату главного квантового числа; это число оказалось равным количеству элементов в периодах периодической таблицы. Модель Бора, таким образом, выявила несомненную связь периодичности свойств элементов со строением электронных оболочек атомов.
Для атома водорода расчёты спектров на основе модели Бора дали хорошее согласие с экспериментом, но для других элементов получалось существенное расхождение с опытными данными. В 1916 г. немецкий физик Арнольд Иоганн Вильгельм Зоммерфельд уточнил модель Бора. Зоммерфельд высказал предположение, что кроме круговых, электрон может двигаться и по эллиптическим орбитам. При этом почти одинаковому уровню энергии соответствует число типов орбит, равное главному квантовому числу. Зоммерфельд дополнил модель побочным (орбитальным) квантовым числом (определяющим форму эллипсов) и зависимостью массы электрона от скорости. Основываясь на модели атома Бора-Зоммерфельда, представляющей собой компромисс между классическими и квантовыми представлениями (в классическую картину вводились квантовые ограничения), Нильс Бор в 1921 г. заложил основы формальной теории периодической системы. Причина периодичности свойств элементов, по мнению Бора, заключалась в периодическом повторении строения внешнего электронного уровня атома.
Для
того, чтобы объяснить, почему имеет
место квантование энергетических
уровней (существование стационарных
орбит), в 1924 г. де
Бройлембыла выдвинутагипотеза,
что каждая движущаяся частица одновременно
обладает свойствами волны,
длина
которой ![]() .Эта
гипотеза основывалась на последних
достижениях физики того времени
(например, было уже известно, что свет
имеет двойственную
природу, обладая свойствамиэлектромагнитной
волныи одновременно свойствами
потока частиц –фотонов).
Гипотеза де Бройля экспериментально
подтверждаетсядифракцией
электронов в кристаллахи позволяет
объяснить существование стационарных
орбит. Электрон может без потери энергии
находиться на тех орбитах, в которых
укладывается целое число волн де Бройля.
В этом случае соблюдается условие
существованиястоячей
волны.
.Эта
гипотеза основывалась на последних
достижениях физики того времени
(например, было уже известно, что свет
имеет двойственную
природу, обладая свойствамиэлектромагнитной
волныи одновременно свойствами
потока частиц –фотонов).
Гипотеза де Бройля экспериментально
подтверждаетсядифракцией
электронов в кристаллахи позволяет
объяснить существование стационарных
орбит. Электрон может без потери энергии
находиться на тех орбитах, в которых
укладывается целое число волн де Бройля.
В этом случае соблюдается условие
существованиястоячей
волны.
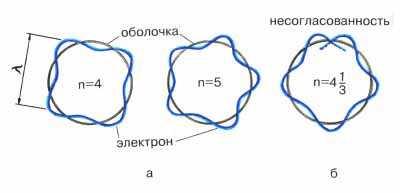
Рис.2. Разрешенные (а) и неразрешенные (б) стоячие волны электрона на боровских орбитах. Стоячие волны на круговой орбите могут существовать только при условии, что длина орбиты равна целому числу длин волн. В случае (б) это условие не соблюдается и волна гасит сама себя. Такая модель наглядно показывает, что квантовое число nможет быть только целым.
Возможность рассматривать каждую частицу одновременно как волну называется корпускулярно-волновым дуализмом. Из него вытекает соотношение неопределенностей Гейзенберга. Согласно классической механике, движение материальной точки однозначно описывается значениями координат и импульсаИмпульсом называется произведение массы объекта на его скорость: p = mv. В случае микрообъектов, когда движение происходит в соответствии с законами квантовой механики, описать координаты и скорость с любой точностью принципиально невозможно.Гейзенбергустановил, что координаты и импульсИмпульсом называется произведение массы объекта на его скорость: p = mv можно определить с ограниченной точностью x+x; p+p, причем x и p – это не ошибки измерения, а принципиально обусловленные неопределенности величин. Соотношение неопределенностейимеет вид неравенстваxph и также позволяет объяснить устойчивость атома. Будем считать, что движение электронав атоме водорода H происходит в области пространства радиусаr. Тогда неопределенность в его положении можно принять равной r. Если попытаться локализовать электрон на ядре (x0), то неопределенность импульса будет неограниченно возрастать (p). Таким образом, “падение” электрона на ядро, допустимое с точки зрения классической механики, в действительности оказывается невозможным. Для примера допустим, что положение электрона определено с точностью 0,001 нм = 0,00110–9 м. Тогда неопределенность в скорости его движения составит огромную величину 58000 км/с.
Волновое уравнение. Квантовомеханическое объяснение строения атома
Неопределенность установления положения и скорости электрона столь велика, что необходимо вообще отказаться от анализа траектории его движения. Однако есть возможность вероятностного описания строения атома.
Согласно квантовой механике, движение электрона в атоме описывается волновым уравнением (уравнение Шредингера):
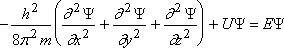 ,
,
где – волновая функция;
m – масса покоя электрона me=9,109.10-31 кг;
U – потенциальная энергия;
E – полная энергия электрона;
x, y, z – координаты.
Решением уравнения Шредингера является волновая функция и соответствующее ей значение энергии электрона E. Вероятность нахождения электрона в пространстве характеризуется квадратом волновой функции, т.е. величиной 2. Для описания строения атома можно рассматривать электрон как бы “размазанным” в пространстве в виде электронного облака. Величина 2, полученная из волнового уравнения, является мерой электронной плотности в данном элементе объема, или мерой вероятности нахождения электрона в данном элементе объема атома.
Таким образом, в квантовомеханической (вероятностной) модели атома исчезает смысл орбиты, на которой находится электрон. Взамен ее мы имеем дело с электронной плотностью, “размазанной” в пространстве атома. Тело, образованное “размазанным” электроном, называют орбиталью. Обычно под орбиталью понимают часть пространства, заключающую 90% электронного облака.
Наличие трех измерений пространства приводит к тому, что в выражении волновой функции , являющейся решением уравнения Шредингера, появляются три величины, которые могут принимать только дискретные целочисленные значения – три квантовых числа. Они обозначаются символами n, l и ml. Эти квантовые числа характеризуют состояние электрона не только в атоме водорода, но и в любом другом атоме.
Характеристика электронов квантовыми числами.
а) Главное квантовое число (n) определяет средний радиус электронного облака, или общую энергию электрона на данном уровне. Оно принимает натуральные значения от 1 до . В реальных атомах n имеет 7 значений, обозначаемых латинскими буквами K, L, M, N, O, P, Q. Значение n=1 отвечает уровню с самой низкой энергией (т.е. наиболее устойчивому состоянию электрона). Теоретически количество уровней не ограничено, но в атоме главным образом бывают заняты электронами уровни с низкой энергией.