ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 23.08.2024
Просмотров: 2221
Скачиваний: 1
СОДЕРЖАНИЕ
Основные понятия и законы химии Атомно - молекулярное учение.
Закон сохранения массы веществ
Составление химических уравнений
Расчеты по химическим уравнениям
Закон Авогадро и молярный объем газа
Основные классы неорганических
2. Разложение некоторых кислородсодержащих веществ (оснований, кислот, солей) при нагревании:
Графическое изображение формул
Химическое равновесие. Константа химического равновесия
Энергия Гиббса направленность химических процессов
Примеры термодинамических расчетов
Химическая кинетика. Скорость химической реакции
Молекулярность элементарных реакций
Смещение химического равновесия
3 Влияние температуры на положение равновесия
Основные характеристики растворов
Растворимость газов в жидкостях
Взаимная растворимость жидкостей
Растворимость твердых веществ в жидкостях
1. Давление насыщенного пара разбавленных растворов
2. Давление пара идеальных и реальных растворов
3. Температура кристаллизации разбавленных растворов
4. Температура кипения разбавленных растворов
5. Осмотическое давление разбавленных растворов
6. Понятие активности растворенного вещества
Слабые электролиты. Константа диссоциации
Количественные характеристики процесса гидролиза соли.
Направленность реакций в растворах электролитов
Протонная теория Брёнстеда-Лоури
Коррозия металлов и методы защиты металлов от коррозии
Волновое уравнение. Квантовомеханическое объяснение строения атома
Электронная структура атомов и периодическая система элементов
Структура периодической системы элементов д.И. Менделеева.
Периодичность свойств химических элементов и их соединений
Ковалентная связь. Метод валентных связей
Способы образования ковалентной связи
Гибридизация атомных орбиталей
Квантовомеханические теории строения комплексных соединений
2. Гибридизация орбиталей и структура комплексов
.
Фазовые равновесия
Вещество при изменении давления и температуры может переходить из одного агрегатного состояния в другое. Эти переходы, совершающиеся при постоянной температуре, называют фазовыми переходами первого рода. Количество теплоты, которое вещество получает из окружающей среды либо отдает окружающей среде при фазовом переходе, есть скрытая теплота фазового перехода. Если рассматривается гетерогенная система, в которой нет химических взаимодействий, а возможны лишь фазовые переходы, то при постоянстве температуры и давления в системе существует т.н. фазовое равновесие. Фазовое равновесие характеризуется некоторым числом фаз, компонентов и числом степеней термодинамической свободы системы.
Компонент – химически однородная составная часть системы, которая может быть выделена из системы и существовать вне её. Число независимых компонентов системы равно числу компонентов минус число возможных химических реакций между ними.
Число степеней свободы – число параметров состояния системы, которые могут быть одновременно произвольно изменены в некоторых пределах без изменения числа и природы фаз в системе.
Число степеней свободы гетерогенной термодинамической системы, находящейся в состоянии фазового равновесия, определяется правилом фаз, сформулированным Дж. Гиббсом:
Число степеней свободы равновесной термодинамической системы С равно числу независимых компонентов системы К минус число фаз Ф плюс число внешних факторов, влияющих на равновесие.
Для системы, на которую из внешних факторов влияют только температура и давление, можно записать:
С = К – Ф + 2
Системы принято классифицировать по числу компонентов (одно-, двухкомпонентные и т.д.), по числу фаз (одно-, двухфазные и т.д.) и числу степеней свободы (инвариантные, моно-, дивариантные и т.д.). Для систем с фазовыми переходами обычно рассматривают графическую зависимость состояния системы от внешних условий – т.н. диаграммы состояния.
Анализ диаграмм состояния позволяет определить число фаз в системе, границы их существования, характер взаимодействия компонентов. В основе анализа диаграмм состояния лежат два принципа: принцип непрерывности и принцип соответствия. Согласно принципу непрерывности, при непрерывном изменении параметров состояния все свойства отдельных фаз изменяются также непрерывно; свойства системы в целом изменяются непрерывно до тех пор, пока не изменится число или природа фаз в системе, что приводит к скачкообразному изменению свойств системы. Согласно принципу соответствия, на диаграмме состояния системы каждой фазе соответствует часть плоскости – поле фазы. Линии пересечения плоскостей отвечают равновесию между двумя фазами. Всякая точка на диаграмме состояния (т. н. фигуративная точка) отвечает некоторому состоянию системы с определенными значениями параметров состояния.
Рассмотрим и проанализируем диаграмму состояния воды . Поскольку вода – единственное присутствующее в системе вещество, число независимых компонентов К = 1. В системе возможны три фазовых равновесия: между жидкостью и газом (линия ОА – зависимость давления насыщенного пара воды от температуры), твердым телом и газом (линия ОВ – зависимость давления насыщенного пара надо льдом от температуры), твердым телом и жидкостью (линия ОС – зависимость температуры плавления льда от давления). Три кривые имеют точку пересечения О, называемую тройной точкой воды; тройная точка отвечает равновесию между тремя фазами.
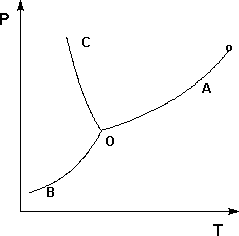
Рис. Диаграмма состояния воды
В тройной точке система трехфазна и число степеней свободы равно нулю; три фазы могут находиться в равновесии лишь при строго определенных значениях температуры и давления (для воды тройная точка отвечает состоянию с Р = 6.1 кПа и Т = 273.16 К).
Кривая ОВ теоретически продолжается до абсолютного нуля, а кривая давления насыщенного пара над жидкостью ОА заканчивается в критической точке воды (Tкр = 607.46 К, Ркр = 19.5 МПа); выше критической температуры газ и жидкость не могут существовать как отдельные фазы. Кривая ОС в верхней части (при высоких давлениях) изменяет свой наклон (появляются новые кристаллические фазы, плотность которых, в отличие от обычного льда, выше, чем у воды).
Внутри каждой из областей диаграммы (АОВ, ВОС, АОС) система однофазна; число степеней свободы системы равно двум (система дивариантна), т.е. можно одновременно изменять и температуру, и давление, не вызывая изменения числа фаз в системе:
С = 1 – 1 + 2 = 2
На каждой из линий число фаз в системе равно двум и, согласно правилу фаз, система моновариантна, т.е. для каждого значения температуры имеется только одно значение давления, при котором система двухфазна:
С = 1 – 2 + 2 = 1.
Кривая равновесия "твердое вещество – жидкость" на диаграммах состояния воды и висмута наклонена влево, а на диаграммах состояния остальных веществ – вправо. Это связано с тем, что плотность воды больше, чем плотность льда (и плотность жидкого висмута больше его плотности в твердом состоянии), т.е. плавление сопровождается уменьшением объема (ΔV < 0).
Основные характеристики растворов
Существование абсолютно чистых веществ невозможно – всякое вещество обязательно содержит примеси, или, иными словами, всякая гомогенная система многокомпонентна. Если имеющиеся в веществе примеси в пределах точности описания системы не оказывают влияния на изучаемые свойства, можно считать систему однокомпонентной; в противном случае гомогенную систему считают раствором.
Раствор – гомогенная система, состоящая из двух или более компонентов, состав которой может непрерывно изменяться в некоторых пределах без скачкообразного изменения её свойств.
Раствор может иметь любое агрегатное состояние; соответственно их разделяют на твердые, жидкие и газообразные (последние обычно называют газовыми смесями). Обычно компоненты раствора разделяют на растворитель и растворенное вещество. Как правило, растворителем считают компонент, присутствующий в растворе в преобладающем количестве либо компонент, кристаллизующийся первым при охлаждении раствора; если одним из компонентов раствора является жидкое в чистом виде вещество, а остальными – твердые вещества либо газы, то растворителем считают жидкость. С термодинамической точки зрения это деление компонентов раствора не имеет смысла и носит поэтому условный характер. Как правило, процессы растворения сопровождаются изменением объема и температуры. Например, при смешении равных объемов этилового спиртаиводыобъем смеси меньше суммы объемов компонентов (это явление называется контракцией).
Одной из важнейших характеристик раствора является его состав, описываемый с помощью понятия концентрация раствора. Ниже дается определение наиболее распространенных способов выражения концентрации и формулы для пересчета одних концентраций в другие: Если для разрушения структуры вещества необходимо больше теплоты, чем ее образуется при гидратации, то растворение - эндотермический процесс. Это происходит, например, при растворении в воде NаNОз, KCl, K2S04, NH4Cl и др.
При работе с растворами необходимо знать их количественный состав. Количественный состав растворов выражается различными способами:
1. Массовая доля ω–число граммов растворенного вещества в 100 граммах раствора.Например, форма записи «раствор NaCl с массовой долейω(NaCl) = 25%» означает, что 25 г NaClсодержится в 100 г раствора. Масса воды в нем равна 75 г
Массовая доля растворенного вещества ω(Х) - безразмерная величина, равная отношению массы вещества m(Х) к массе раствора m(р-ра):
ω(Х)
=
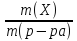 (1)
(1)
m(р-ра) = m(Х) + m(растворителя).
Массовую долю выражают в долях единицы или в процентах.
.
2. Молярная концентрацияС(X)– число молейnрастворенного вещества в одном литре раствора. Молярная концентрация равна отношению химического количества растворенного вещества (п(Х), моль) к объему раствора (V, л):
С(Х)
=
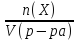 (2)
(2)
Химическое количество вещества выражается соотношением
n(Х)
=
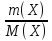 (3)
(3)
где m(Х) - масса вещества Х, г; М(Х) - молярная масса вещества Х, г/моль.
Подставляя формулу (3) в (2), получаем
С(Х)=
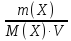 (4)
(4)
(5)
Если известна масса т и плотность ρ раствора, то его объем V
V= ρ m(р-ра) (5)
Молярная концентрация выражается в моль/л или вмоль/дм3 (эта размерность часто обозначается М). Например: 2 М NaOH или C(NaOH) = 2 моль/л. Данная форма записи означает, что 2 моля NaOH содержится в 1 л раствора.
3.
Молярная
концентрация эквивалента (нормальная
концентрация)
С(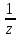 X)
– число молей эквивалентов растворенного
вещества nэкв.
в
одном литре раствора.
X)
– число молей эквивалентов растворенного
вещества nэкв.
в
одном литре раствора.
Молярная
концентрация эквивалента равна отношению
химического количества вещества
эквивалента n(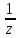 X)
или (nэквX)
к объёму раствора V(л):
X)
или (nэквX)
к объёму раствора V(л):
С(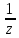 Х)=
Х)=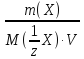 (4)
(4)
Молярная
концентрация эквивалента
выражается
в моль/л или моль/дм3
(часто обозначается н.).
Например: 2 н. Na2SO4
или С(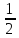 Na2SO4)
=
2
моль/л. Данная форма записи означает,
что 2 моль эквивалента
Na2SO4
содержится в 1 л раствора.
Na2SO4)
=
2
моль/л. Данная форма записи означает,
что 2 моль эквивалента
Na2SO4
содержится в 1 л раствора.
Если взаимодействуют растворы веществ с известными нормальными концентрациями, то в точке эквивалентности справедливы соотношения:
n(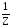 (Х))
=n(
(Х))
=n(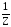 (Y));
(Y));
С(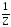 (Х))V(X)
= С(
(Х))V(X)
= С(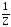 (Y))V(Y).
(Y))V(Y).