ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 23.08.2024
Просмотров: 2243
Скачиваний: 1
СОДЕРЖАНИЕ
Основные понятия и законы химии Атомно - молекулярное учение.
Закон сохранения массы веществ
Составление химических уравнений
Расчеты по химическим уравнениям
Закон Авогадро и молярный объем газа
Основные классы неорганических
2. Разложение некоторых кислородсодержащих веществ (оснований, кислот, солей) при нагревании:
Графическое изображение формул
Химическое равновесие. Константа химического равновесия
Энергия Гиббса направленность химических процессов
Примеры термодинамических расчетов
Химическая кинетика. Скорость химической реакции
Молекулярность элементарных реакций
Смещение химического равновесия
3 Влияние температуры на положение равновесия
Основные характеристики растворов
Растворимость газов в жидкостях
Взаимная растворимость жидкостей
Растворимость твердых веществ в жидкостях
1. Давление насыщенного пара разбавленных растворов
2. Давление пара идеальных и реальных растворов
3. Температура кристаллизации разбавленных растворов
4. Температура кипения разбавленных растворов
5. Осмотическое давление разбавленных растворов
6. Понятие активности растворенного вещества
Слабые электролиты. Константа диссоциации
Количественные характеристики процесса гидролиза соли.
Направленность реакций в растворах электролитов
Протонная теория Брёнстеда-Лоури
Коррозия металлов и методы защиты металлов от коррозии
Волновое уравнение. Квантовомеханическое объяснение строения атома
Электронная структура атомов и периодическая система элементов
Структура периодической системы элементов д.И. Менделеева.
Периодичность свойств химических элементов и их соединений
Ковалентная связь. Метод валентных связей
Способы образования ковалентной связи
Гибридизация атомных орбиталей
Квантовомеханические теории строения комплексных соединений
2. Гибридизация орбиталей и структура комплексов
Положение химического равновесия – это достигнутое при равновесии соотношение концентраций реагирующих веществ, которое неизменно для данного состояния. Количественной характеристикой химического равновесия является константа равновесия, которая может быть выражена через равновесные концентрации С, парциальные давления P.
Состояние химического равновесия описывается законом действующих масс.
При достижении равновесия отношение произведения концентраций (парциальных давлений) продуктов реакции в степенях, соответствующих стехиометрическим коэффициентам, к произведению концентраций исходных веществ также в степенях, соответствующих стехиометрическим коэффициентам, представляет собой константу. Она зависит только от природы реагирующих веществ и температуры. Константа, выраженная через равновесные концентрации Ci обозначается Kс, а выраженная через парциальные давления Pi – Kр.
Для гомогенного процесса
а(А) + b(В) = d(D) + k(K)
Kс
=
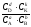 илиKр
=
илиKр
=
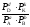 .
.
Для гетерогенного процесса
а(А) + b(В) = с[C] + d(D)
Kс
=
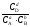 илиKр
=
илиKр
=
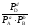 .
.
Концентрация вещества С в процессе взаимодействия не изменяется, поэтому не включается в выражение константы равновесия (С не является действующей массой).
Выражение для Кс и Кр представляет собой математическое выражение закона действующих масс применительно к обратимым процессам.
Используя уравнение Менделеева-Клапейрона РV= (m / M) RT, преобразование которого
РV= nRT
Р= CRT
дает связь между Кс и Кр:
Кр = Кс (RT)n,
n разность между количеством образовавшихся газообразных продуктов и количеством исходных газообразных веществ.
По значению константы химического равновесия можно судить о глубине протекания процесса к моменту достижения равновесия.
В расчетах, связанных с использованием констант равновесия Kс, в предлагаемых задачах используются понятия равновесные и исходные концентрации, изменения концентраций. Равновесными называют концентрации реагирующих веществ в состоянии химического равновесия (С), исходными считают заданные до начала реакции концентрации веществ (С0). Равновесные концентрации реагентов (С) связаны с их исходной концентрацией (С0) уравнением С = С0 – С, где С – количество исходного вещества которое прореагировало до наступления состояния равновесия.
Пример
1.
Равновесие реакции 2(NO)
+ (O2)
= 2(NO2)
установилось при следующих концентрациях
реагирующих веществ: CNO
=
0,02 моль/л; СО = 0,01 моль/л; СNO
= 0,01 моль/л; СNO =
0,01 моль/л. Вычислить константу равновесия
и исходные концентрации NO
и О2.
=
0,01 моль/л. Вычислить константу равновесия
и исходные концентрации NO
и О2.
Решение. Для расчета константы химического равновесия подставим значения равновесных концентраций всех реагирующих веществ в выражение Kс:
Kс
=
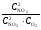 =
=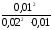 = 0,25.
= 0,25.
Найдем
исходные концентрации NO
и O2
по соотношению С0
= С
+ С.
Для определения исходных концентраций
каждого из веществ нужно
вычислить значения С.
Из уравнения
реакции видим, что из 2 молей NO
в результате реакции образуется 2 моля
NО2,
следовательно, на образование 0,01 моля
NО2
к моменту установления равновесия
расходовалось 0,01 моля NО.
Равновесная концентрация NO
составляет 0,02 моль/л, значит, C0(NO)
= 0,02 + 0,01 = 0,03 моль/л. Рассуждая аналогично,
получим значение СО =
0,005 моль/л, так как по уравнению реакции
1 моль О2
расходуется при образовании 2 молей
NО2.
C0(О
=
0,005 моль/л, так как по уравнению реакции
1 моль О2
расходуется при образовании 2 молей
NО2.
C0(О )
= 0,01 + 0,005 = 0,015 моль/л.
)
= 0,01 + 0,005 = 0,015 моль/л.
Пример 2. Исходные концентрации оксида углерода (IV) и водорода равны соответственно 6 моль/л и 4 моль/л. Константа равновесия процесса (СО2) + (Н2) = (СО) + (Н2О) равна 0,5. Вычислить равновесные концентрации всех веществ.
Решение. Запишем выражение константы равновесия:
Kс
=
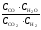 .
.
Обозначим
ССО ,
концентрацию прореагировавшего
СО2
к моменту равновесия за х.
Тогда ССО
,
концентрацию прореагировавшего
СО2
к моменту равновесия за х.
Тогда ССО = 6 – х.
С 1 молем СО2
взаимодействует 1 моль
Н2,
поэтому
количество прореагировавшего водорода
в реакции также будет х, СН
= 6 – х.
С 1 молем СО2
взаимодействует 1 моль
Н2,
поэтому
количество прореагировавшего водорода
в реакции также будет х, СН = 4 – х.
= 4 – х.
Из уравнения реакции следует, что из 1 моля СО2 образуется 1 моль СО, а из 1 моля водорода – 1 моль Н2О, следовательно, концентрации образовавшихся веществ будут равны по х (моль/л).
Подставив значения равновесных концентраций в выражение константы, решим его относительно х:
0,5
=
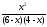 ,
откудах
= 2 моль/л.
,
откудах
= 2 моль/л.
Значит, количество прореагировавших СО2 и Н2 и образовавшихся СО и Н2О составляет 2 моль/л.
Равновесные концентрации СО2 и Н2 соответственно равны:
6 – 2 = 4 моль/л и 4 – 2 = 2 моль/л.
Пример 3. Исходная концентрация вещества А в системе (А) = 2(В) составляет 2 моль/л. Равновесие установилось, когда прореагировало 20% исходного вещества. Вычислить константу равновесия процесса.
Решение. Запишем выражение константы равновесия:
Kс
=
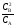 .
.
Вычислим значения равновесных концентраций веществ А и В. Из условия задачи следует, что количество прореагировавшего вещества А составляет 20% от исходного количества, т. е. СА = = 0,2 2 = 0,4 моль/л. Равновесная концентрация вещества А определяется как разность С0(А) – СА = 2 – 0,4 = 1,6 моль/л. Из 1 моля А образуется 2 моля В. Следовательно, если к моменту установления равновесия расходовано 0,4 моль/л вещества А, то образовалось 0,8 моль/л вещества В. Тогда СВ = 0,8 моль/л.
Подставим значения равновесных концентраций в выражение константы равновесия и получим величину константы:
Kс
=
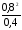 = 1,6.
= 1,6.
Энтропия
Возможность
самопроизвольного протекания химического
процесса определяется двумя факторами:
стремлением системы к понижению
внутренней энергии за счет экзотермической
реакции (-H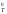 )
и стремлением системы к увеличению
неупорядоченности в расположении частиц
за счет теплового движения. При
низких температурах преобладает
стремление к минимуму энергии. При
высоких температурах за счет усиления
хаотического движения частиц вещества
главную роль начинает играть фактор
повышения неупорядоченности,
мерой которой является функция состояния,
называемая энтропией.
)
и стремлением системы к увеличению
неупорядоченности в расположении частиц
за счет теплового движения. При
низких температурах преобладает
стремление к минимуму энергии. При
высоких температурах за счет усиления
хаотического движения частиц вещества
главную роль начинает играть фактор
повышения неупорядоченности,
мерой которой является функция состояния,
называемая энтропией.
Энтропия (S) - термодинамическая функция, однозначно характеризующая состояние системы независимо от ее предыстории. Она является количественной мерой неупорядоченности системы, мерой хаотического движения и взаимного расположения частиц. Энтропия зависит от природы вещества, его количества (концентрации), давления и температуры. В отличие от внутренней энергии и энтальпии можно определить абсолютное значение энтропии.
В изолированных системах (где обмен с окружающей средой энергией и массой невозможен) процессы самопроизвольно протекают лишь в сторону повышения энтропии (второе начало термодинамики). Т.е. в изолированных системах изменение энтропии может использоваться для определения направления самопроизвольного протекания процесса.
Энтропия вещества в определенном состоянии (при заданных параметрах) в определенном агрегатном состоянии (газ, жидкость, твердое) пропорциональна логарифму термодинамической вероятности нахождения вещества в этом состоянии (уравнение Больцмана):
S = k ln W,
Где k = R / NA , W – термодинамическая вероятность состояния, которая определяется числом микросостояний, с помощью которых может быть реализовано данное макросостояние.
В идеальном кристалле при абсолютном нуле Т=0К, движение прекращается, положение частиц остается неизменным, и вероятность состояния системы может быть только одна. Следовательно, энтропия идеального кристалла при абсолютном нуле S=0.
Третье начало термодинамики гласит, что энтропия беспримесного идеального кристаллического тела при температуре 0 К равна нулю.
Стандартной считается энтропия, отнесенная к 1 молю вещества при стандартных условиях (давление 1 атм (101,32 кПа) и температура 298 К (25 ОС)). Значения стандартных энтропий для большинства химических соединений представлены в справочной литературе. Единицей измерения энтропии, как правило, является Джоуль на моль-кельвин (Дж /( моль К)).
Зависимость энтропии от температуры связана с теплоемкостью изобарного (р = const и Δр = О) процесса (ΔСр ) и определяется (если считать теплоемкость величиной, не зависящей от температуры) следующим уравнением:
![]()
Поскольку
S0
незначительно зависит от температуры,
то S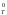
S
S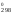 .
.
Оценить знак изменения энтропии в различных процессах можно, даже не проводя расчетов, а основываясь лишь на логических размышлениях.
Так, при подводе тепла неупорядоченность в расположении отдельных структурных единиц системы увеличивается, и энтропия растет. Степень увеличения неупорядоченности системы и рост ее энтропии зависят от количества подведенной теплоты и температуры. В ходе превращения твердого вещества в жидкое, а затем в газообразное, неупорядоченность системы, а следовательно, и энтропия увеличиваются ( ΔS> О ), так как возможности поступательного, колебательного, вращательного движения в системе существенно возрастают. Процессы испарения, плавления, расширения газа, разрыва связей между атомами сопровождаются увеличением энтропии. Процессы, сопровождающиеся увеличением упорядоченности системы: конденсация, кристаллизация, сжатие, упрочнение связей, полимеризация и т. п. приводят к уменьшению энтропии.
Для
различных процессов изменение стандартной
энтропии (S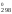 )
рассчитывают по формуле:
)
рассчитывают по формуле:
S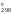 =
=
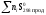 –
–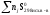 .
.
Обозначения:
S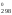 (S
(S )
– изменение стандартной энтропии
реакции.
)
– изменение стандартной энтропии
реакции.
S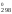 – стандартная энтропия вещества или
иона.
– стандартная энтропия вещества или
иона.
S – стандартная энтропия вещества или
иона при температуре, отличной от 298К.
– стандартная энтропия вещества или
иона при температуре, отличной от 298К.
Размерность
S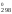 – Дж/(К моль); S
– Дж/(К моль); S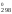 – Дж/К.
– Дж/К.
Так
как энтропия растет с повышением
температуры, то можно считать, что мера
беспорядка определяется произведением
Т
S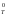 (энтропийный
фактор)
(энтропийный
фактор)