ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 31.03.2024
Просмотров: 1100
Скачиваний: 0
СОДЕРЖАНИЕ
Математическое моделирование элементов сложных экологических систем
Лекция 1. Введение в моделирование. Исторический экскурс.
1. Основы моделирования в экологии 1.1. Общие принципы построения моделей в экологии
2.2. Этапы построения математической модели
1.4. Элементы теории подобия, применяемые в моделировании
3.2.2. Выборочный метод в экологометрике.
Зависимость числа интервалов от объема выборки
Статистический ряд по интервалам
Лекция 4. Статистические оценки параметров распределения случайных величин по выборкам
4.4. Статистические оценки гипотез об экологических моделях
Выборка из генеральной совокупности
Статистическая таблица эксперимента
Пример преобразования членов уравнения регрессии
Вычисление данных для линеаризации уравнения регрессии
Нормальные уравнения мнк для некоторых функций
Статистическое оценивание уравнения регрессии и парной корреляции.
Обработка результатов наблюдений
Рекомендации по выбору вида функции
3.4. Динамические статистические модели
Данные по объему сброса качественных сточных вод
Данные по объему сброса сточных вод за 5-летие
Пример расчета 5-летних средних
Расчетные значения для определения уравнения динамики
Ряд динамики для определения сезонных колебаний
Эксперименталъный материал исследования
8.1. Анализ влияния отдельных факторов в экологической модели.
Лекция 9. Методы оптимизации. Метод Лагранжа
Лекция 10. Метод линейного программирования.
Лекция 11. Функциональные модели.
Лекция 12. Модели процессов содержащие обыкновенные дифференциальные уравнения.
Численные ошибки использованных для вычисления данных
Лекция 13. Статистические модели динамики.
Лекция 16. Информационные технологии в экологии. Экологические информационные системы.
1 6.1. Экологические информационные системы
1. Какова область значения для числовых характеристик?
Лекция 17. Использование информационных технологий для решения задач экологии.
Критические значения коэффициента корреляции rk;α
2.1. Подобие физических явлений и его признаки
2.4. Применение методов подобия в математическом
11.3. Численные методы решения дифференциальных уравнений
11.3.2. Процесс численного решения
11.3.4. Модифицированный метод Эйлера
11.3.6. Метод Рунге – Кутта для систем дифференциальных уравнений
11.3.7. Общая характеристика одношаговых методов
11.3.9. Методы прогноза и коррекции
11.3.10. Краткая характеристика методов прогноза и коррекции.
11.3.11. Выбор шага и погрешность решения.
11.4. Имитационное моделирование систем
11.4.1. Принципы имитационного моделирования
11.4.3. Динамическая модель исследуемого объекта
11.4.4. Построение имитационных моделей динамических систем
11.4.5. Преобразование передаточных функций звеньев в дифференциальные уравнения в форме Коши
11.4.6. Синтез имитационной модели на основе структурной схемы
11.5. Теоретические основы построения математических моделей систем
11.5.1. Компонентные и топологические уравнения
11.5.2. Компонентные и топологические уравнения механической системы
11.5.3. Компонентные и топологические уравнения электрической системы
11.5.4. Компонентные и топологические уравнения гидравлической системы
11.5.5. Компонентные и топологические уравнения тепловой системы
11.6.1. Сущность метода электроаналогий.
11.6.2. Электромеханические аналогии
11.6.3. Построение имитационных моделей методом электроаналогий
11.6.4. Плоское прямолинейное движение звеньев
11.6.5. Электрогидравлические аналогии
F = f (m,l,t),
где F - сила; m - масса; l - расстояние; t - время.
Размерности параметров в классе MLT (масса, длина, время) выражаются следующими соотношениями:
[F] = LMT -2 , [m] = M, [l] = L, [t] = T.
Легко видеть, что определяющие параметры m, l и t имеют независимые размерности, размерность же параметра F выражается через размерности первых трех
[F] = [m] [l] [t-2].
Таким образом, n = k = 3 и анализ размерности дает выражение для критерия подобия
![]() ,
,
что совпадает с результатом, который был получен для этой задачи в примере 2.1.
Пример 2.4
Определим с помощью П -теоремы критерий подобия для электрической цепи, которая была рассмотрена в примере 2.3. Цепь содержит активное сопротивление R и индуктивность L. При включении цепи на постоянное напряжение U в ней протекает процесс, который можно записать в виде функциональной зависимости
U = f (t,i,R,L).
Допустим, что определяющие параметры t,i,R имеют независимые размерности
[t] = T, [i] = I , [R] = L2MT-3I-2.
Тогда параметры U и L будут размерно-зависимыми.
[U] = L2MT-3I-1, [L] = L2MT-2 I-2 .
В данном случае k = 3, n - k =1. Анализируя размерности параметров, находим критерии подобия.

Заметим, что в примерах 2.3 и 2.4 критерии подобия найдены на основе общих функциональных зависимостей между определяющими и определяемыми параметрами. Точные уравнения физических зависимостей нами не рассматривались. Независимость физической закономерности (2.14) от выбора
единиц измерения означает, что эту зависимость можно представить
в виде уравнения
![]()
Уменьшение числа аргументов упрощает исследование. Пусть в уравнении (2.14) для выяснения зависимости величины a от некоторого определяющего параметра ai надо измерить эту величину при десяти значениях данного аргумента. Тогда для экспериментального нахождения величины a - как функции n определяющих параметров a1,…, an - следует произвести 10n экспериментов.
Согласно П - теореме, если все величины a1,a2 ,…,an выражаются через k независимых размерностей, задача сводится к определению функции n - k безразмерных аргументов П1, …, Пn-k, для нахождения которых достаточно 10n-k опытов, т.е. в 10k раз меньше. Трудоемкость установления искомой функции сокращается на столько порядков, сколько среди определяющих параметров величин с независимыми размерностями.
В примере 2.4 исходное уравнение можно заменить зависимостью
П = Ф (П1).
Следовательно, в координатах П, П1 все опытные точки должны располагаться на единой кривой. Таким образом, заранее проведенный анализ размерностей сокращает объем экспериментальной работы во много раз.
Пример 2.5
Пусть известно, что период T колебаний маятника не зависит от его начального отклонения и скорости, а определяется лишь его длиной l, массой m и ускорением свободного падения g . Функциональная связь
T = f (l,m, g )
содержит четыре размерных величины. Допустим, что определяющие параметры l, m и g имеют независимые размерности.
[l] = L, [m] = M, [g] = LT -2.
Тогда параметр T следует принять размерно-зависимым.
[T ] = T.
Анализируя размерности, находим критерий подобия
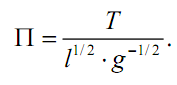
Здесь, k = n = 3. Следовательно, выражение f (l,m, g ) = const и
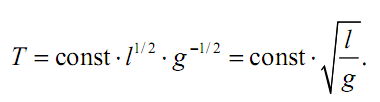
С точностью до безразмерного множителя данная формула дает решение колебаний маятника. Причем выясняется, что их период не зависит от m. Таким образом, анализ размерностей дает возможность получить ценную предварительную информацию о процессе, не находя полностью решения задачи.
Пример 2.6
При атомном взрыве в его центре мгновенно выделяется значительная энергия E . От центра взрыва распространяется мощная ударная волна. Радиус фронта ударной волны r через промежуток времени τ после взрыва зависит от E, τ и плотности воздуха ρ [11].
r = f (E,τ,ρ).
Таким образом, n = 3, а размерности определяющих параметров в классе MLT есть:
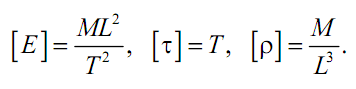
В данном случае k = n = 3, так что функция f (E,τ,ρ) = const. Критерий подобия
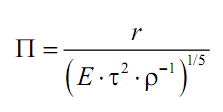
и
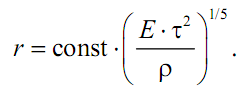
Эта формула показывает, что если измерить тем или иным способом радиус ударной волны в разные моменты времени, то в логарифмических координатах (5/2)lg(r), lg(τ) экспериментальные точки должны располагаться на прямой
![]()
имеющей наклон, равный единице. Более детальный анализ показывает, что эта const =1. В 1950 г. английский физик Джеффри Ингрем Тейлор обработал
кинофильм о распространении огненного шара, снятый во время американских испытаний ядерного взрыва в Нью-Мехико в 1945 г., и определил, что энергия взрыва равнялась примерно 1017Дж.
Публикация Тейлором этой величины вызвала в свое время смущение в американских официальных кругах. В различных уравнениях математической физики (задачах гидродинамики, переноса тепла, диффузии, химической кинетики) появляются своеобразные частные решения, которые при изменении времени преобразуются одно из другого по правилу подобия. Такие решения называются автомодельными. Наиболее важное свойство автомодельного решения состоит в том, что зависимость от аргументов входит через единственный комплекс. Благодаря этому уравнение в частных производных можно привести к обыкновенному дифференциальному уравнению. Его интегрирование существенно проще, чем нахождение решения начально-граничной задачи. В сложных нелинейных задачах получение автомодельного решения зачастую остается единственно возможным средством найти аналитическую зависимость и понять качественные особенности явления. Более подробные сведения об автомодельных решениях можно найти в литературе [2], [9].
назад
11.3. Численные методы решения дифференциальных уравнений
11.3.1. Постановка задачи
Дифференциальными называются уравнения, содержащие одну или несколько производных. Инженеру очень часто приходится сталкиваться с ними при разработке новых изделий или технологических процессов, так как большая часть законов физики формулируется именно в виде дифференциальных равнений. Любая задача проектирования, связанная с расчетом потоков энергии или движением тел, в конечном счете, сводится к решению дифференциальных уравнений. Лишь очень немногие из них удается решить без помощи вычислительных машин. Поэтому численные методы решения дифференциальных уравнений играют такую важную роль в практике инженерных расчетов и в моделировании.
Так при реализации цифровых систем управления инженеру-системотех-нику приходится решать дифференциальные уравнения в реальном масштабе времени, т.е. непосредственно в процессе управления объектом. Примером могут служить цифровые регуляторы в системах управления электроприводами металлорежущих станков и промышленных роботов, а также цифровые системы управления автомобильными и авиационными двигателями, летательными аппаратами, морскими судами и т.д.
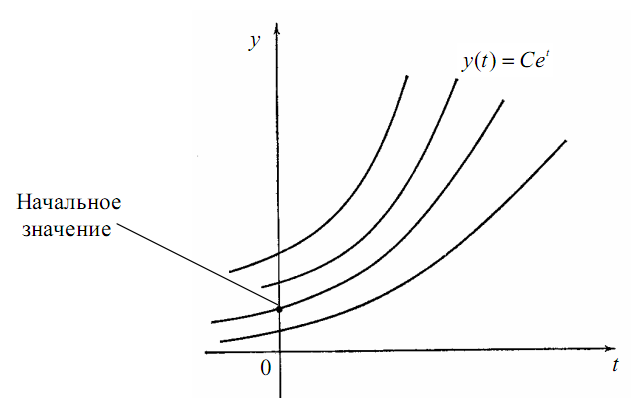
Рис. 11.3.1. Решения дифференциального уравнения
Известные математические программы – MathCAD, Matlab, Mathematica и др. непригодны для решения таких задач. Эти программы занимают в ЭВМ много памяти и, кроме того, они не могут работать в реальном масштабе времени. Поэтому для построения компактных, работающих в реальном времени цифровых моделей и систем инженеру приходится самостоятельно разрабатывать алгоритмы и программы для решения дифференциальных уравнений тем или иным численным методом.
В зависимости от числа независимых переменных и, следовательно, типа входящих в них производных дифференциальные уравнения делятся на две различные категории:
обыкновенные, содержащие одну независимую переменную и производные по ней, и уравнения в частных производных, содержащие несколько независимых переменных и производные по ним, которые называют частными.
Рассмотрим методы решения обыкновенных дифференциальных уравнений (ОДУ). Дифференциальное уравнение первого порядка можно записать в виде
y' = f(y,t).
Это уравнение имеет семейство решений y(t) . Например, если f(y,t) = y , то для произвольной константы С функция y(t) = Cet является решением (рис.3.1). Выбор начального значения, скажем y(0) , служит для выделения одной кривой из семейства кривых. Зачастую имеется более чем одна зависимая переменная, и тогда задача заключается в решении системы уравнений первого порядка, например,
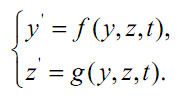
Решение этой системы содержит две постоянные интегрирования, и, следовательно, нужны два начальных условия, чтобы определить эти константы.
Если значения y и z указаны при одном и том же значении независимой переменной t0, то система будет иметь единственное решение. Задача определения y и z для будущих значений t > t0 называется задачей с начальными условиями или задачей Коши. Если же условия задаются при двух или более значениях независимой переменной, то задача называется краевой. В задаче Коши дополнительные условия называют начальными, а в краевой задаче – граничными.
Любое обыкновенное дифференциальное уравнение порядка n, которое можно записать так, что его левая часть есть производная наивысшего порядка, а в правой части эта производная не встречается, может быть записана из n уравнений первого порядка путем введения n-1 новых переменных.
Например, уравнение
u'' = g(u,u' t)
можно записать как систему
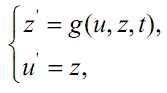
где z'(t) = u''(t).
При обсуждении методов для задачи Коши удобно представлять
себе единственное уравнение
y '= f(y,t)
с начальным условием y(t0 ) = y0. Однако методы с равным успехом применимы и к системам уравнений. Часто в задаче Коши в роли независимой переменной выступает время.
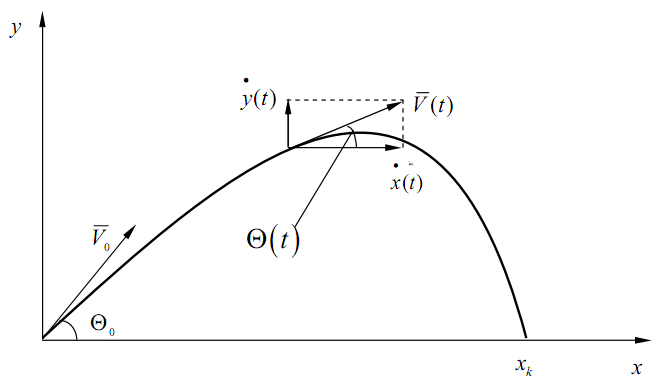
Рис 3.2. К задаче о траектории
Пример 3.1
Примером может служить задача о траектории. Предположим, что снаряд выпускается с начальной скоростью V0 под заданным углом наклона Q0 к поверхности.
Как видно из рис.
3.2 функции x(t)
и y(t)
обозначают координаты x
и у
снаряда в
момент времени t,
а функции
![]() и
и
![]() определяют его скоростьV
(t
) .
определяют его скоростьV
(t
) .