Файл: Математическое моделирование в экологии.doc

Составим уравнение равновесия сил:

(6.13)

где

Составим уравнение равновесия моментов:

M_T1+ M_T2 - M_T3 - M_u = 0, (6.14)

где M_Т1 = T₁ × l; M_Т2 = T₂ × l/2; M_Т3 = T₃ × l.

На основании данных уравнений составляем эквивалентную электрическую схему (рис. 6.30).

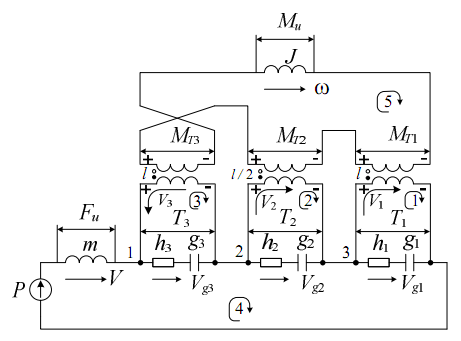
Рис. 6.30

Электрическая схема содержит 5 контуров, 3 узла и 3 трансформатора. Уравнения Кирхгофа для контуров 1-5 совпадают с уравнениями равновесия сил и с уравнениями равновесия моментов (6.13-6.14). Записываем уравнения Кирхгофа для узлов 1, 2 и 3.

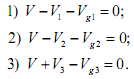
Записываем уравнения трансформаторов.

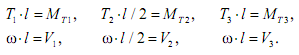
В данной математической модели соотношения для скоростей изменений токов, протекающих через обмотки трансформаторов, не используются. Поэтому в уравнениях трансформаторов этих соотношений нет.

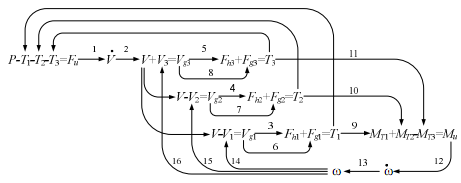
Рис. 6.31

Рассматриваемое твердое тело имеет две степени свободы, так как оно может совершать прямолинейное и одновременно вращательное движения. Поэтому чтобы построить сеть связей динамической системы, необходимо в двух уравнениях Кирхгофа для контуров вынести вправо инерционные составляющие. Такими уравнениями являются уравнения (6.13) и (6.14). Используя дополнительно уравнения Кирхгофа для узлов 1–3, а также уравнения трансформаторов, строим сеть связей динамической системы (рис.6.31).

Таблица 6.9

Передаточные функции элементарных звеньев

Теперь можно построить структурную схему динамической системы. С этой целью каждую ветвь сети связей заменяем элементарным звеном. Передаточные функции элементарных звеньев приведены в табл. 6.9, а структурная схема на рис. 6.32.

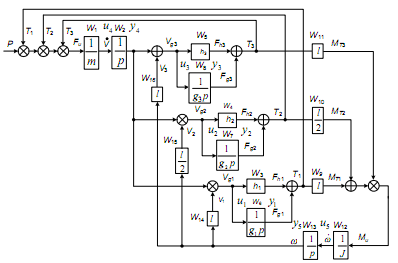
Рис. 6.32

В соответствии со структурной схемой записываем уравнения связей и дифференциальные уравнения элементарных звеньев.

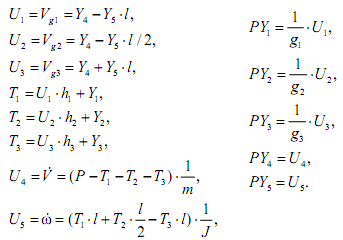
На рис.6.33 представлена программа моделирования рассмотренного механического объекта в математической среде MathCAD.

Вал на трех опорах

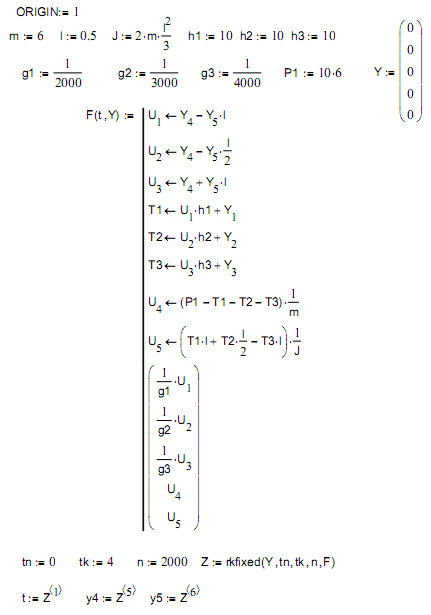
Рис. 6.33. Код программы моделирования в системе MathCAD

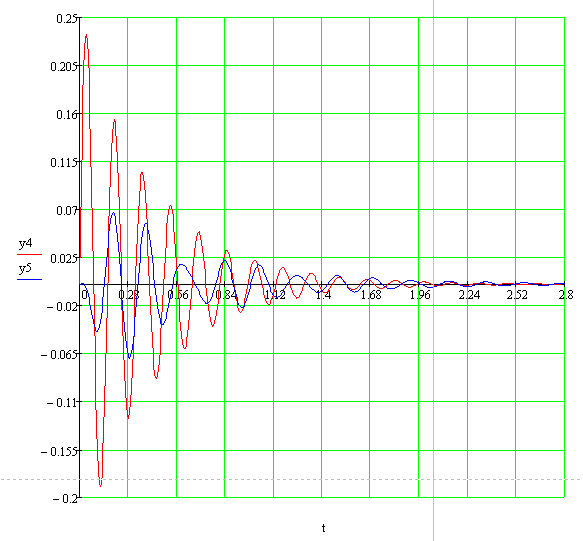
Рис. 6.33 а. График процесса при h1=h2=h3=10.

Результаты моделирования представлены в виде графиков линейных (рис. 6.34, а)

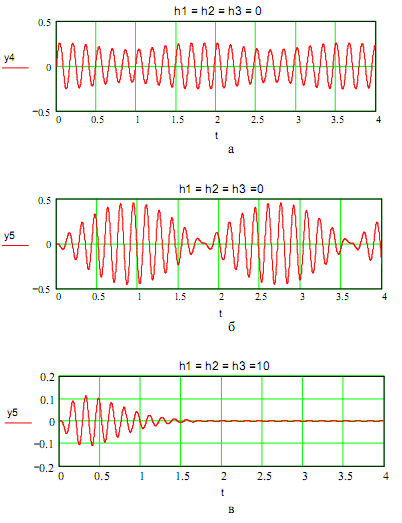
Рис.6.34

и угловых (рис. 6.34, б) скоростей движений объекта при отсутствии демпфирования. На рис. 6.34, в показано движение объекта, когда коэффициенты демпфирования не равны нулю.

11.6.5. Электрогидравлические аналогии

Требуется построить имитационную модель гидростатической опоры. Конструктивная схема незамкнутой гидростатической опоры представлена на рис. 6.35.

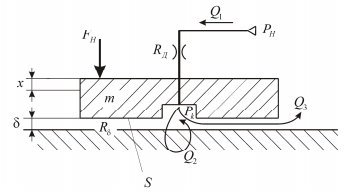
Рис. 6.35. Конструктивная схема гидростатической опоры

Гидростатические опоры используются в качестве гидростатических направляющих в тяжелых и средних металлорежущих станках. Их широкое применение обусловлено малыми силами трения при перемещении механизма, высоко нагрузочной способностью, надежностью и долговечностью, так как исключается контакт между подвижной и неподвижной частями опоры. Принцип действия незамкнутых гидростатических направляющих заключается в следующем. Масло от насоса под постоянным давлением P_H подается через дроссель с постоянным

сопротивлением R_δ в карман-камеру. Из кармана масло под давлением вытесняется через зазор δ , гидравлическое сопротивление которого

В состоянии покоя равнодействующая от давления масла в кармане и в зазоре уравновешивает внешнюю нагрузку F_H. При увеличении нагрузки зазор уменьшается на величину х. При этом расход масла через карман снижается и соответственно возрастает давление в кармане. Этот процесс продолжается до тех пор, пока равнодействующая от давления масла не уравновесит возросшую нагрузку при новой (уменьшенной) величине зазора в направляющих. При уменьшении нагрузки на направляющую зазор увеличивается, и давление в кармане уменьшается до тех пор, пока не наступит положение равновесия при возросшей величине зазора.

При оптимальных соотношениях параметров гидростатических направляющих изменение толщины масляного слоя при изменяющейся нагрузке оказывается достаточно малым, что позволяет применять эти направляющие в высокоточных станках. Расход масла через дроссель – Q₁. Через щель вытесняется количество масла Q₃. При постоянном давлении насоса и сопротивлении дросселя расход Q₁ постоянен, но при движении платформы вверх-вниз расход масла через щель изменяется. Это связано с изменением объема под платформой. При уменьшении

объема излишек масла вытесняется из-под платформы, а при его увеличении под платформой создается вакуум и масло «втягивается» в карман. Это приводит к появлению мнимого расхода масла Q₂, который, складываясь с расходом Q₁, дает расход масла на выходе Q₃. Наличие этого мнимого расхода обусловливает уникальное свойство гидравлических систем – демпфирование колебаний. Распределение давления в зазоре показано на рис. 6.36.

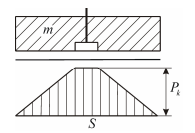
Рис. 6.36. Распределение давления в зазоре

В соответствии с эпюрой результирующая гидростатическая сила в зазоре равна:

где S_ЭФ - эффективная площадь.

Используя метод электроаналогии, перейдем от конструктивной схемы к эквивалентной электрической схеме, сохраняя при этом обозначения физических величин конструктивной схемы (рис.6.37).

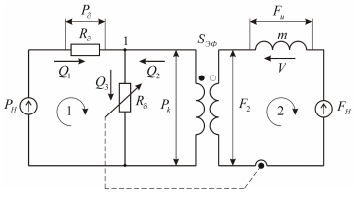
Рис. 6.37. Эквивалентная электрическая схема

Запишем уравнения Кирхгофа для контуров 1 и 2, а также для узла 1:

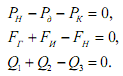
Уравнения трансформатора:

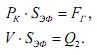
На основе составленных уравнений строим сеть связей физических величин (рис. 6.38).

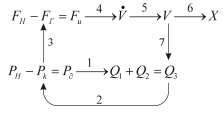
Рис. 6.38. Сеть связей

Таблица 6.10

Передаточные функции элементарных звеньев

Передаточные функции элементарных звеньев (табл.6.10). Заменяя в сети связи соединительные стрелки выражениями для передаточных функций, получаем структурную схему математической модели (рис. 6.37).

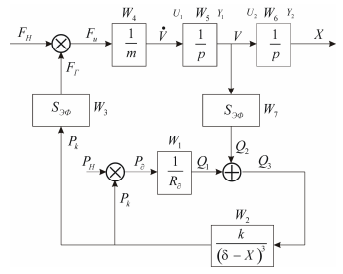
Рис. 6.39. Структурная схема

Запишем дифференциальные уравнения интегрирующих звеньев.

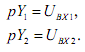
Далее формируем уравнения связи. С этой целью сначала определим давление в кармане P_K:

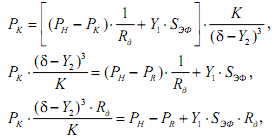
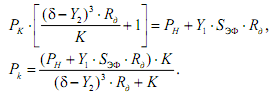
Откуда:

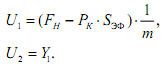
Расчёт исходных параметров модели.

Дано:

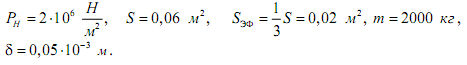
Примем для установившегося режима

Тогда

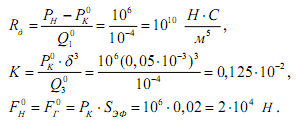
Результаты моделирования гидростатических направляющих представлены в виде графиков, которые показывают реакцию системы на внешнее усилие F_H= 3×10⁴H (рис. 6.40)

Рис. 6.40