Файл: Математическое моделирование в экологии.doc

Рассмотрим второй случай — метод наименьших квадратов для нелинейных форм. Пусть Y — целевая функция; у₁, у₂, ..., у_n — набор ее наблюдений; х₁, х₂, ..., х_n — переменные факторы. Наблюдения представляют из себя вектор

X_i = (x_1i, x_2i, ..., x_mi).

Необходимо целевую функцию Y выразить через вектор Х посредством функции f, вид которой известен, однако неизвестны некоторые её параметры d₁, d₂, ..., d_k. Тогда для Y_i можно записать

Y_i = f_i(d₁, d₂, ..., d_k; x₁, x₂, ..., x_mi) + F_i ,

где F_i — отклонение (ошибка).

Если исключить параметры d₁, d₂, ..., d_k то функция запишется в виде

Y_i = f_i(х„.,х„,,х„„.) + F_i,

куда входят параметры, которые необходимо найти МНК.

Минимизируя

и используя метод Маркварда, введем векторы

; ; ; ,

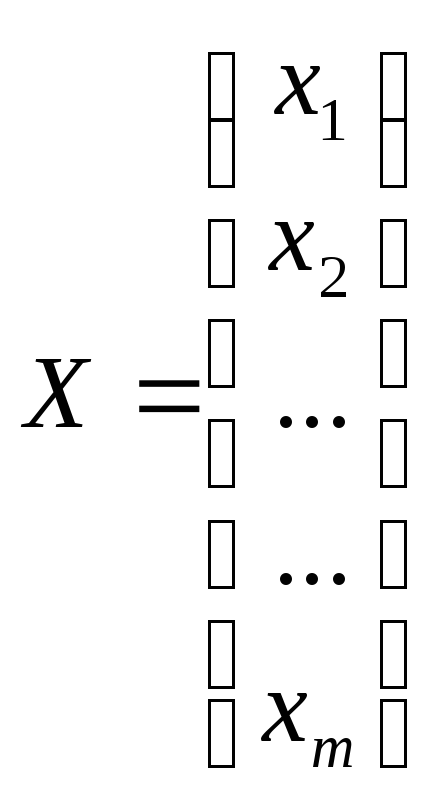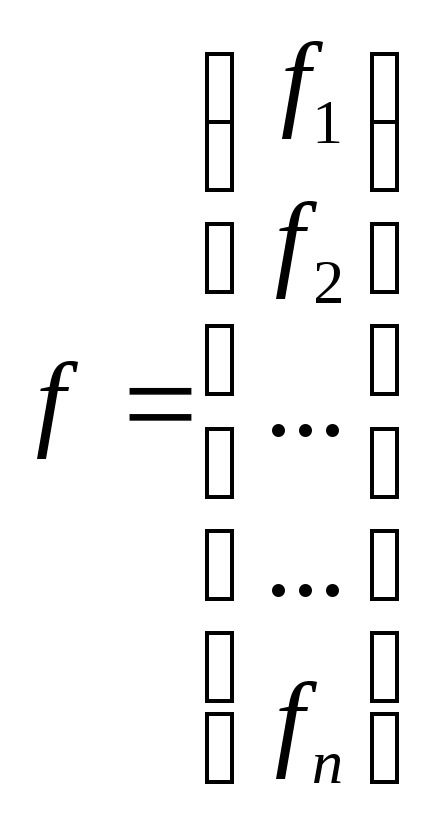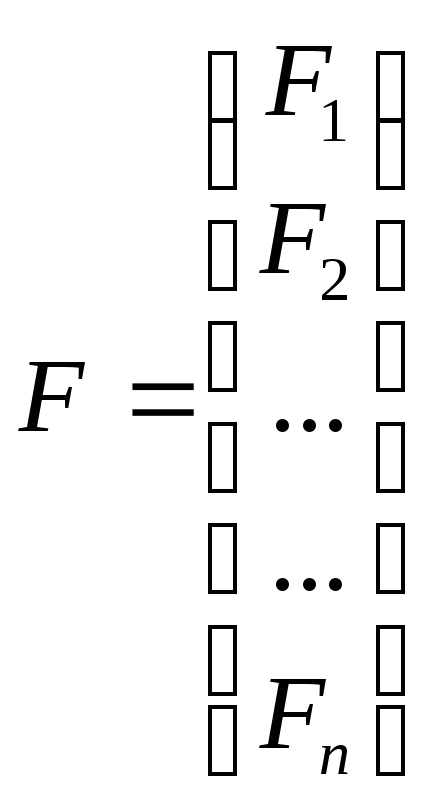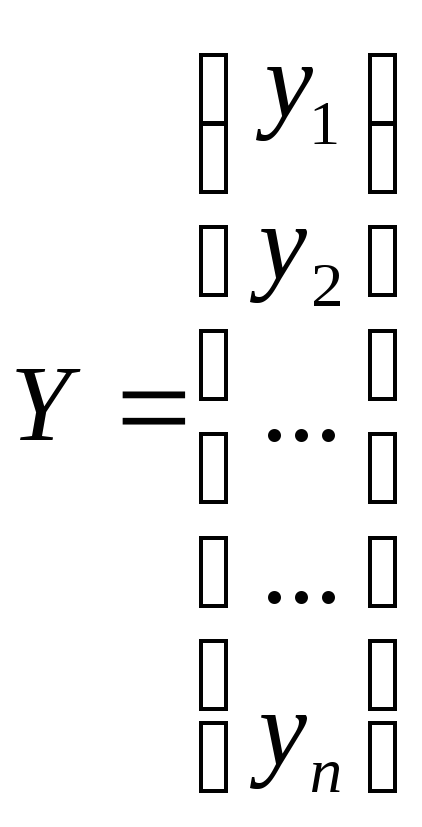сформируем задачу в виде: найти такое Х*, что при F = Y — f целевая функция (сумма квадратов остатков) S = F^TF минимизируется.

Приближенное значение Х_i, получаемое на t-том шаге итеративного процесса, и последующее приближенное значение Х_t+1 связаны между собой вектором поправки ∆Х, т.е.

Формула вектора поправки ∆Х согласно условию минимизации, выводится из решения системы линейных уравнений

откуда = -(А^TА)^-1 A^тF,

где А — первая частная производная от F, определяемая как матрица Якоби 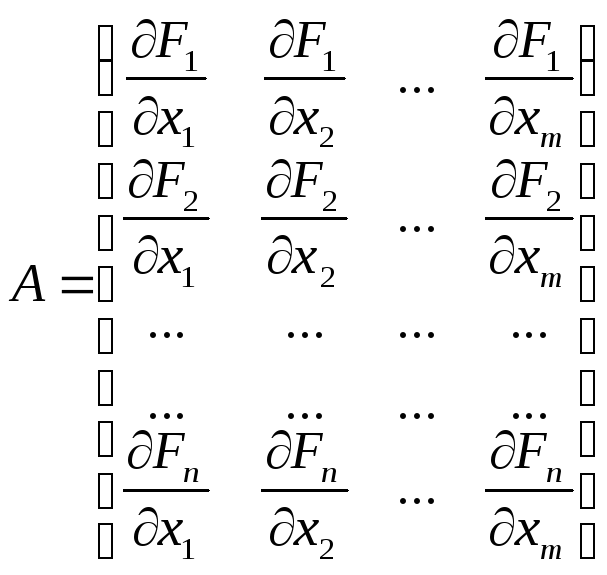приx=x_t

Это формулы итерации по методу Ньютона — Гаусса. При их использовании, если степень нелинейности f(х) высока, а стартовое значение х далеко отстоит от минимизирующего значения, то велика вероятность «раскачки» и расходимости итеративного процесса.

Левенберг и Марквардт в процедуре Ньютона — Гаусса предложили искать корректирующий вектор ∆Х из уравнения

(A^тA +v²I) ∆Х = - А^тF;

где I — единичная матрица, а v— некоторая величина, называемая числом Марквардта. Тогда

∆Х = -( A^тА + v²I)^-1 А^тF.

При v = 0 приходим к формуле ∆Х= -( A^тА + v²I)^-1 А^тF. При вычислениях рекомендуется за начальное значение принимать v =0,001, затем на каждом шаге увеличивать v в десять раз, до тех пор, пока S не начнет уменьшаться.

Статистическое оценивание уравнения регрессии и парной корреляции.

После построения уравнения регрессии по МНК проводят оценивание значимости коэффициентов уравнения регрессии и коэффициента корреляции, а также значимость уравнения в целом. Рас- смотрим оценивание на примере полученного уравнения у = 0,71+1,07x по результатам эксперимента, зафиксированного в табл. 3.2.

1. Для статистического оценивания коэффициентов уравнения регрессии проверяют нулевую гипотезу Н: В = 0, т.е. отличается ли статистически значимо оценка коэффициента регрессии от нуля. Границу значимости устанавливают по критерию Стьюдента:

где b — выборочная оценка коэффициента уравнения регрессии;

В — значение коэффициента уравнения регрессии в генеральной совокупности;

S(b) — среднее квадратическое отклонение коэффициента b;

—значение критерия Стьюдента при числе степеней свободы n - 2 и уровне значимости α (см. приложение 2).

Если условие выполняется, то гипотезу Н₀: В = 0 отклоняют, т.е. коэффициент уравнения регрессии значимо отличается от нуля.

Пример. По данным примера в табл. 3.2 произвести статистическую оценку коэффициентов уравнения регрессии

= 0,71+ 1,07х.

Р е ш е н и е. Вычисляем статистику для коэффициентов b₀ и b₁.

где средние квадратические отклонения вычисляем по формулам:

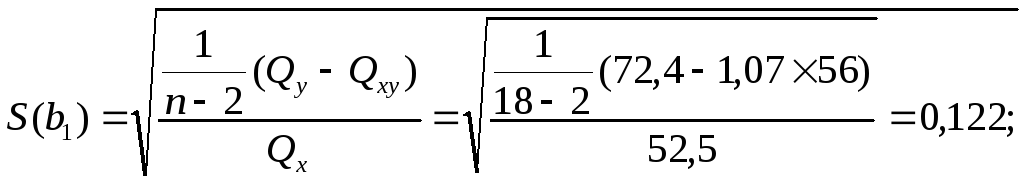
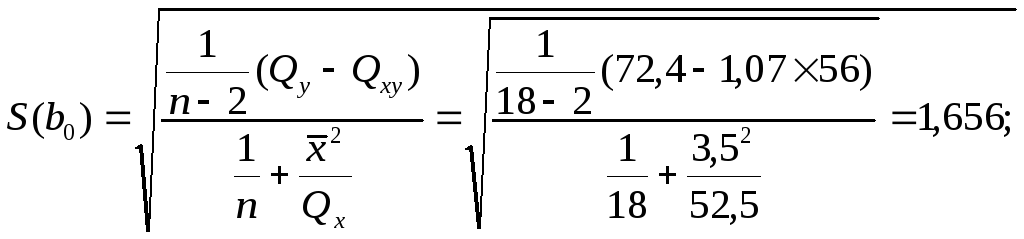
При числе степеней свободы k = n — 2 = 18 — 2 = 16 и уровне значимости,

α = 0,1 по таблице (см. приложение 2) определяем значение критерия Стьюдента

Сравниваем:

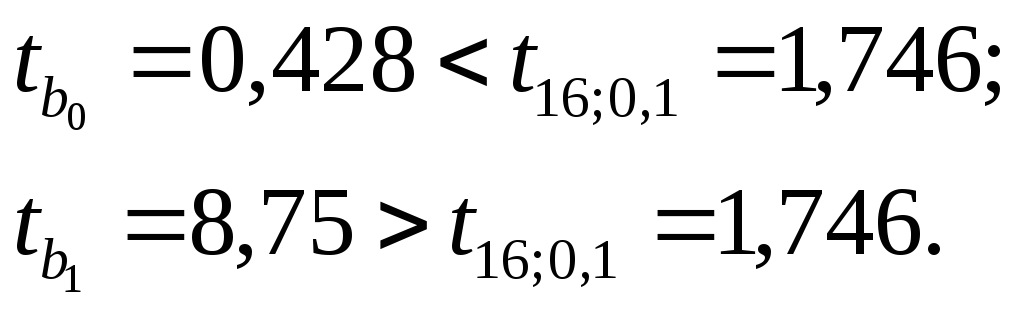
Отсюда делаем заключение, что коэффициент b₀ незначим, т.е. принимается гипотеза Н₀: В = О, а коэффициент b₁ значим, т.е. гипотеза Н₀: В = 0 отклоняется. Тогда уравнение регрессии из вида должно быть преобразовано в уравнение с доверительной вероятностью (надежностью) Р = 0,9.

2. Для статистического оценивания коэффициента корреляции проверяют нулевую гипотезу Н₀: R = 0, где R — коэффициент корреляции в генеральной совокупности. Границу значимости устанавливают по критерию Стьюдента

Если это условие выполняется, то гипотезу Н₀: R = 0 отклоня- ют, т.е. коэффициент r принимается значимым.

Пример. По данным примера в табл. 3.2 следует определить значимость коэффициента корреляции r= 0,987.

Р е ш е н и е. Вычисляем статистику t для коэффициента корреляции

При уровне значимости α = 0,1 и числе степеней свободы n - 2 = 18 - 2 = 16 по таблице (см. приложение 2) выбираем значение

При условии t_r = 24,56 > t_16;0,1 = 1,746 гипотеза H₀: R = 0 отклоняется, т.е. полученный коэффициент корреляции является значимым.

3. Для проверки значимости полученного уравнения регрессии, т.е. его адекватности результатам эксперимента, используют критерий Фишера

где — дисперсия случайной величины Y,

—остаточная дисперсия,

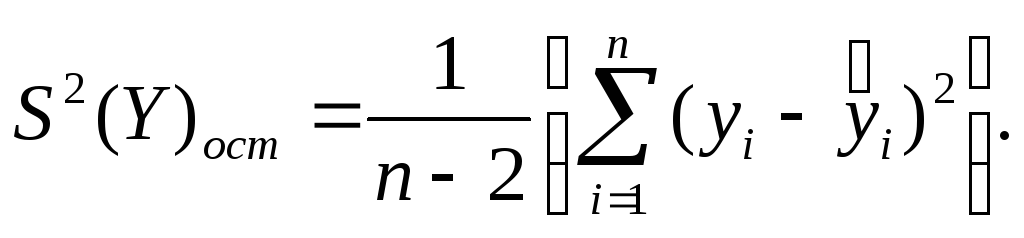
Величина у вычисляется для каждого из n по формуле = b₀ + b₁х_i, а затем находится разность экспериментального и теоретического у_i значения по всем n экспериментам. Остаточная дисперсия имеет важное значение в статистических исследованиях, так как она представляет собой показатель ошибки предсказания уравнением регрессии результатов опыта.

Критерий находится по таблице (см. приложение 6) по заданному уровню значимости а, числу степеней свободы k₁ для S²(Y) и k₂ для S²(Y)_ост принимают для n испытаний: k₁ = n — 1; k₂ = n — 2. Если условие F_b > F_k1;k2;a выполняется, то уравнение регрессии адекватно описывает статистические данные, т.е. оно статистически значимо для полученных в результате эксперимента данных.

Пример. Проверить значимость уравнения регрессии y=1,067х по данным, вычисленным по табл. 3.2 при b₀ = 0 и b₁ = 1,067.

Р е ш е н и е. Вычисляем F_b статистику