ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 31.03.2024
Просмотров: 1109
Скачиваний: 0
СОДЕРЖАНИЕ
Математическое моделирование элементов сложных экологических систем
Лекция 1. Введение в моделирование. Исторический экскурс.
1. Основы моделирования в экологии 1.1. Общие принципы построения моделей в экологии
2.2. Этапы построения математической модели
1.4. Элементы теории подобия, применяемые в моделировании
3.2.2. Выборочный метод в экологометрике.
Зависимость числа интервалов от объема выборки
Статистический ряд по интервалам
Лекция 4. Статистические оценки параметров распределения случайных величин по выборкам
4.4. Статистические оценки гипотез об экологических моделях
Выборка из генеральной совокупности
Статистическая таблица эксперимента
Пример преобразования членов уравнения регрессии
Вычисление данных для линеаризации уравнения регрессии
Нормальные уравнения мнк для некоторых функций
Статистическое оценивание уравнения регрессии и парной корреляции.
Обработка результатов наблюдений
Рекомендации по выбору вида функции
3.4. Динамические статистические модели
Данные по объему сброса качественных сточных вод
Данные по объему сброса сточных вод за 5-летие
Пример расчета 5-летних средних
Расчетные значения для определения уравнения динамики
Ряд динамики для определения сезонных колебаний
Эксперименталъный материал исследования
8.1. Анализ влияния отдельных факторов в экологической модели.
Лекция 9. Методы оптимизации. Метод Лагранжа
Лекция 10. Метод линейного программирования.
Лекция 11. Функциональные модели.
Лекция 12. Модели процессов содержащие обыкновенные дифференциальные уравнения.
Численные ошибки использованных для вычисления данных
Лекция 13. Статистические модели динамики.
Лекция 16. Информационные технологии в экологии. Экологические информационные системы.
1 6.1. Экологические информационные системы
1. Какова область значения для числовых характеристик?
Лекция 17. Использование информационных технологий для решения задач экологии.
Критические значения коэффициента корреляции rk;α
2.1. Подобие физических явлений и его признаки
2.4. Применение методов подобия в математическом
11.3. Численные методы решения дифференциальных уравнений
11.3.2. Процесс численного решения
11.3.4. Модифицированный метод Эйлера
11.3.6. Метод Рунге – Кутта для систем дифференциальных уравнений
11.3.7. Общая характеристика одношаговых методов
11.3.9. Методы прогноза и коррекции
11.3.10. Краткая характеристика методов прогноза и коррекции.
11.3.11. Выбор шага и погрешность решения.
11.4. Имитационное моделирование систем
11.4.1. Принципы имитационного моделирования
11.4.3. Динамическая модель исследуемого объекта
11.4.4. Построение имитационных моделей динамических систем
11.4.5. Преобразование передаточных функций звеньев в дифференциальные уравнения в форме Коши
11.4.6. Синтез имитационной модели на основе структурной схемы
11.5. Теоретические основы построения математических моделей систем
11.5.1. Компонентные и топологические уравнения
11.5.2. Компонентные и топологические уравнения механической системы
11.5.3. Компонентные и топологические уравнения электрической системы
11.5.4. Компонентные и топологические уравнения гидравлической системы
11.5.5. Компонентные и топологические уравнения тепловой системы
11.6.1. Сущность метода электроаналогий.
11.6.2. Электромеханические аналогии
11.6.3. Построение имитационных моделей методом электроаналогий
11.6.4. Плоское прямолинейное движение звеньев
11.6.5. Электрогидравлические аналогии
Значение критерия
|
Объем выборки |
Уровень значимости, α |
Объем выборки |
Уровень значимости, α |
||||||||
|
n1 |
n2 |
0,005 |
0,010 |
0,025 |
0,050 |
n1 |
n2 |
0,005 |
0,010 |
0,025 |
0,050 |
|
6 |
6 |
23 |
24 |
26 |
28 |
14 |
14 |
147 |
152 |
160 |
166 |
|
6 |
7 |
24 |
25 |
27 |
30 |
14 |
15 |
151 |
156 |
164 |
171 |
|
6 |
8 |
25 |
27 |
29 |
31 |
15 |
15 |
171 |
176 |
184 |
192 |
|
6 |
9 |
26 |
28 |
31 |
33 |
15 |
16 |
175 |
181 |
190 |
197 |
|
6 |
10 |
27 |
29 |
32 |
35 |
15 |
17 |
180 |
186 |
195 |
203 |
|
7 |
7 |
32 |
34 |
36 |
39 |
16 |
16 |
196 |
202 |
211 |
219 |
|
7 |
8 |
34 |
35 |
38 |
41 |
16 |
17 |
201 |
207 |
217 |
225 |
|
7 |
9 |
35 |
37 |
40 |
43 |
16 |
18 |
208 |
212 |
222 |
231 |
|
7 |
10 |
37 |
39 |
42 |
45 |
17 |
17 |
223 |
230 |
240 |
249 |
|
8 |
8 |
43 |
45 |
49 |
51 |
17 |
18 |
228 |
235 |
246 |
255 |
|
8 |
9 |
45 |
47 |
51 |
54 |
17 |
19 |
234 |
241 |
252 |
262 |
|
8 |
10 |
47 |
49 |
53 |
56 |
18 |
18 |
252 |
259 |
270 |
280 |
|
9 |
9 |
56 |
59 |
62 |
66 |
18 |
19 |
258 |
265 |
277 |
287 |
|
9 |
10 |
58 |
61 |
65 |
69 |
18 |
20 |
263 |
271 |
283 |
294 |
|
9 |
11 |
61 |
63 |
68 |
72 |
19 |
19 |
283 |
291 |
303 |
313 |
|
10 |
10 |
71 |
74 |
78 |
82 |
19 |
20 |
289 |
297 |
309 |
320 |
|
10 |
11 |
73 |
77 |
81 |
86 |
20 |
20 |
315 |
324 |
337 |
348 |
|
10 |
12 |
76 |
79 |
84 |
89 |
20 |
21 |
322 |
331 |
344 |
356 |
|
11 |
11 |
87 |
91 |
96 |
100 |
21 |
21 |
349 |
359 |
373 |
385 |
|
11 |
12 |
90 |
94 |
99 |
104 |
21 |
22 |
356 |
366 |
381 |
393 |
|
11 |
13 |
93 |
97 |
103 |
108 |
22 |
22 |
386 |
396 |
411 |
424 |
|
12 |
12 |
105 |
109 |
115 |
120 |
22 |
23 |
393 |
403 |
419 |
432 |
|
12 |
13 |
109 |
113 |
119 |
125 |
23 |
23 |
424 |
434 |
451 |
465 |
|
12 |
14 |
112 |
116 |
123 |
129 |
23 |
24 |
431 |
443 |
459 |
474 |
|
13 |
13 |
125 |
130 |
136 |
142 |
24 |
24 |
464 |
475 |
492 |
507 |
|
13 |
14 |
129 |
134 |
141 |
147 |
24 |
25 |
472 |
484 |
501 |
517 |
|
13 |
15 |
133 |
138 |
148 |
152 |
25 |
25 |
505 |
517 |
536 |
552 |
Приложение 9
Значение функции
![]()
|
X |
x+0 |
x+0,05 |
x+0,1 |
x+0,15 |
|
0,0 |
0,3989 |
0,3984 |
0,3970 |
0,3945 |
|
0,2 |
0,3910 |
0,3867 |
0,3814 |
0,3752 |
|
0,4 |
0,3910 |
0,3867 |
0,3814 |
0,3752 |
|
0,6 |
0,3332 |
0,3230 |
0,3123 |
0,3011 |
|
0,8 |
0,2897 |
0,2780 |
0,2661 |
0,2541 |
|
1,0 |
0,2420 |
0,2299 |
0,2179 |
0,2059 |
|
1,2 |
0,1942 |
0,1826 |
0,1714 |
0,1604 |
|
1,4 |
0,1497 |
0,1394 |
0,1295 |
0,1200 |
|
1,6 |
0,1109 |
0,1023 |
0,0940 |
0,0863 |
|
1,8 |
0,0790 |
0,0721 |
0,0656 |
0,0596 |
|
2,0 |
0,0540 |
0,0488 |
0,0440 |
0,0396 |
|
2,2 |
0,0355 |
0,0317 |
0,0283 |
0,0252 |
|
2,4 |
0,0224 |
0,0198 |
0,0175 |
0,0154 |
|
2,6 |
0,0136 |
0,0119 |
0,0104 |
0.0091 |
|
2,8 |
0,0079 |
0.0069 |
0,0060 |
0,0051 |
|
3,0 |
0,004 |
0,0038 |
0,0033 |
0,0028 |
|
3,2 |
0,0024 |
0,0020 |
0,0017 |
0,0015 |
|
3,4 |
0,0012 |
0,0010 |
0,0009 |
0,0007 |
|
3,6 |
0,0006 |
0,0005 |
0,0004 |
0,0001 |
|
3,8 |
0,0003 |
0,0002 |
0,0002 |
0,0001 |
|
4,0 |
0.00013 |
0,00010 |
0,000089 |
0,000 007 |
|
4,2 |
0,000056 |
0,000047 |
0,000038 |
0,000 034 |
|
4,4 |
0,000025 |
0,000020 |
0,000016 |
0,000 013 |
|
4,6 |
0,000010 |
0,000008 |
0,000006 |
0,000 005 |
|
4,8 |
0,000004 |
0,000003 |
0,0000024 |
0,000 019 |
|
5,0 |
0,0000015 |
|
|
|
Приложение 10
Критические значения коэффициента корреляции rk;α
|
Число степеней свободы |
Значение г при а = 0,05 |
Значение г при а = 0,01 |
|
1 |
0,9877 |
0,9995 |
|
2 |
0,9000 |
0,9800 |
|
4 |
0,729 |
0,882 |
|
6 |
0,621 |
0,789 |
|
8 |
0,549 |
0,715 |
|
10 |
0,497 |
0,658 |
|
14 |
0,426 |
0,574 |
|
18 |
0,378 |
0,516 |
|
22 |
0,344 |
0,472 |
|
26 |
0,317 |
0,437 |
|
30 |
0,296 |
0,409 |
|
35 |
0,275 |
0,381 |
|
40 |
0,257 |
0,358 |
|
50 |
0,231 |
0,322 |
|
60 |
0,211 |
0,295 |
|
70 |
0,195 |
0,274 |
|
80 |
0,183 |
0,257 |
|
90 |
0,173 |
0,242 |
|
100 |
0,164 |
0,230 |
|
200 |
0,116 |
0,164 |
назад
Приложение 11
2. Основы теории подобия
2.1. Подобие физических явлений и его признаки
Теория подобия рассматривает аналогии в моделировании и определяет методику применения этих аналогий в научном и практическом исследовании. Изучение свойств подобных явлений и методы установления подобия составляют содержание теории подобия физических явлений. Каждому изменению состояния системы, происходящему во времени и пространстве, отвечает ряд процессов или один процесс. При протекании процесса меняются значения переменных, характеризующих состояние системы. Система, в которой происходят процессы, состоит из элементов. Их физические характеристики определяют параметры системы. Для описания процессов необходимо ввести систему координат, в которой записывается математическое уравнение, связывающее между собой переменные и параметры системы. Явления будут подобны друг другу, если существует полное соответствие всех геометрических размеров рассматриваемых систем и всех изменяющихся во времени и пространстве переменных.
Геометрическое соответствие материальных систем означает, что все пространственные координаты одной системы пропорциональны пространственным координатам второй системы. Математически это условие в декартовых координатах записывается следующим образом:
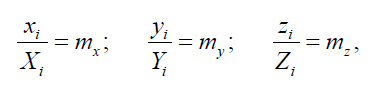
Index.html
где xi, yi, zi, Xi, Yi, Zi - координаты сходственных точек рассматриваемых систем; mx my mz - коэффициенты подобия или масштабы.
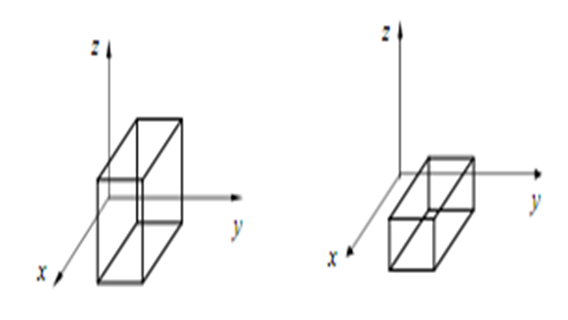
Рис 2.1. Пример Аффинного подобия.
Index2.html
При неравенстве масштабов по координатным осям, т.е. если , mx ≠ my ≠ mz осуществляется так называемое аффинное подобие. Пример аффинного подобия приведен на рис. 2.1. Частным случаем аффинного подобия является геометрическое подобие, при котором масштабы по осям равны. Пример геометрического подобия приведен на рис. 2.2.
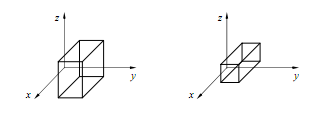
Рис 2.2. Пример геометрического подобия.