ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 31.03.2024
Просмотров: 1079
Скачиваний: 0
СОДЕРЖАНИЕ
Математическое моделирование элементов сложных экологических систем
Лекция 1. Введение в моделирование. Исторический экскурс.
1. Основы моделирования в экологии 1.1. Общие принципы построения моделей в экологии
2.2. Этапы построения математической модели
1.4. Элементы теории подобия, применяемые в моделировании
3.2.2. Выборочный метод в экологометрике.
Зависимость числа интервалов от объема выборки
Статистический ряд по интервалам
Лекция 4. Статистические оценки параметров распределения случайных величин по выборкам
4.4. Статистические оценки гипотез об экологических моделях
Выборка из генеральной совокупности
Статистическая таблица эксперимента
Пример преобразования членов уравнения регрессии
Вычисление данных для линеаризации уравнения регрессии
Нормальные уравнения мнк для некоторых функций
Статистическое оценивание уравнения регрессии и парной корреляции.
Обработка результатов наблюдений
Рекомендации по выбору вида функции
3.4. Динамические статистические модели
Данные по объему сброса качественных сточных вод
Данные по объему сброса сточных вод за 5-летие
Пример расчета 5-летних средних
Расчетные значения для определения уравнения динамики
Ряд динамики для определения сезонных колебаний
Эксперименталъный материал исследования
8.1. Анализ влияния отдельных факторов в экологической модели.
Лекция 9. Методы оптимизации. Метод Лагранжа
Лекция 10. Метод линейного программирования.
Лекция 11. Функциональные модели.
Лекция 12. Модели процессов содержащие обыкновенные дифференциальные уравнения.
Численные ошибки использованных для вычисления данных
Лекция 13. Статистические модели динамики.
Лекция 16. Информационные технологии в экологии. Экологические информационные системы.
1 6.1. Экологические информационные системы
1. Какова область значения для числовых характеристик?
Лекция 17. Использование информационных технологий для решения задач экологии.
Критические значения коэффициента корреляции rk;α
2.1. Подобие физических явлений и его признаки
2.4. Применение методов подобия в математическом
11.3. Численные методы решения дифференциальных уравнений
11.3.2. Процесс численного решения
11.3.4. Модифицированный метод Эйлера
11.3.6. Метод Рунге – Кутта для систем дифференциальных уравнений
11.3.7. Общая характеристика одношаговых методов
11.3.9. Методы прогноза и коррекции
11.3.10. Краткая характеристика методов прогноза и коррекции.
11.3.11. Выбор шага и погрешность решения.
11.4. Имитационное моделирование систем
11.4.1. Принципы имитационного моделирования
11.4.3. Динамическая модель исследуемого объекта
11.4.4. Построение имитационных моделей динамических систем
11.4.5. Преобразование передаточных функций звеньев в дифференциальные уравнения в форме Коши
11.4.6. Синтез имитационной модели на основе структурной схемы
11.5. Теоретические основы построения математических моделей систем
11.5.1. Компонентные и топологические уравнения
11.5.2. Компонентные и топологические уравнения механической системы
11.5.3. Компонентные и топологические уравнения электрической системы
11.5.4. Компонентные и топологические уравнения гидравлической системы
11.5.5. Компонентные и топологические уравнения тепловой системы
11.6.1. Сущность метода электроаналогий.
11.6.2. Электромеханические аналогии
11.6.3. Построение имитационных моделей методом электроаналогий
11.6.4. Плоское прямолинейное движение звеньев
11.6.5. Электрогидравлические аналогии
Поскольку
Qi = Ni qi
то имеют место равенства
-
Q1 = N1 q1
Q2 = N2 q2
Q3 = N3 q3
………..
Qn = Nn qn
(2.7)
Теперь подставим равенства (2.7) в уравнение (2.3а)
![]()
В соответствии с уравнением Фурье
N1 = N2 =…..= Nn
т.е.
![]()
В результате от уравнения (2.3а) приходим к уравнению (2.4а).
Следовательно, уравнения (2.3а) и (2.4а) оказываются тождественными. Это означает, что между соответствующими членами уравнений (2.3а) и (2.4а) существуют соотношения:
![]() ;
;
![]() ;
…….
;
…….
![]()
Обобщая полученные результаты на S подобных процессов, получаем
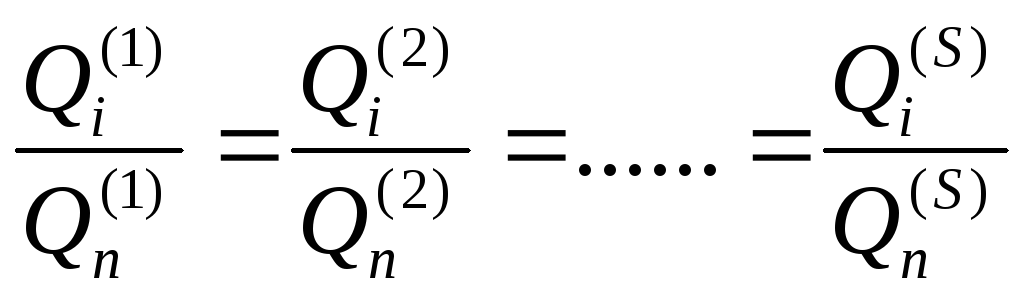
где 1,2, …, S – номер процесса.
Индексы, характеризующие номер процесса, можно опустить и
записать (2.9) в общем виде
![]() ,
,
где idem - означает "соответственно одинаково для всех рассматриваемых процессов". Таким образом, у подобных процессов некоторые соотношения
параметров, называемые критериями подобия, оказались численно
одинаковыми. В сложных явлениях может одновременно протекать несколько различных процессов. Подобие каждого из этих процессов в отдельности обеспечивает подобие всего явления.
Обозначая критерий подобия буквой П (пи), можно дать краткую формулировку первой теоремы: для всех подобных явлений
П = idem.
Следует заметить, что справедливо и обратное положение: если критерии подобия численно одинаковы, то явления подобны. Нужно обратить внимание на практически важное свойство критериев подобия: критерии подобия любого явления могут преобразовываться в критерии другой формы, получаемые за счет операции умножения или деления ранее найденных критериев друг на друга или на какой-либо из них, т.е. если какие-либо критерии
Пk = idem и Пk+j = idem
то очевидно
Пk
Пk+j
= idem;
![]() ;
;
![]() ;
kПkj
= idem.
;
kПkj
= idem.
где k - любая постоянная величина.
Заметим, что уравнение (2.3а) могло иметь совершенно иную физическую природу, чем уравнение (2.4а) при одинаковой их математической записи.
Пример 2.1
Пусть имеются два тела массой М1 и М2 , движения которых подобны и описываются следующими однородными уравнениями:
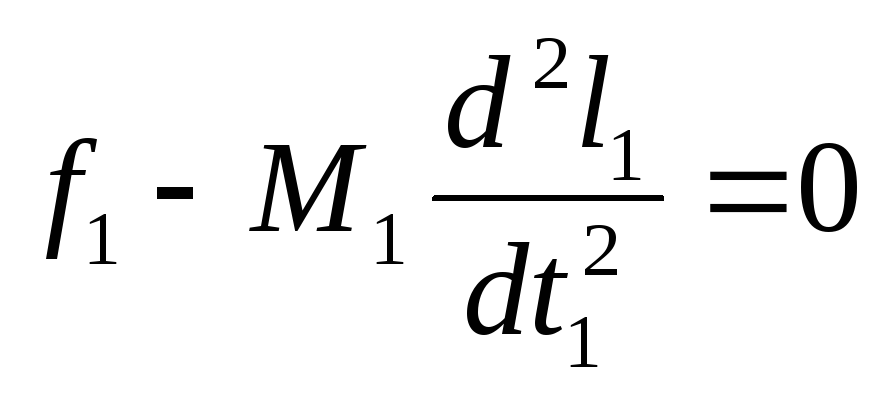
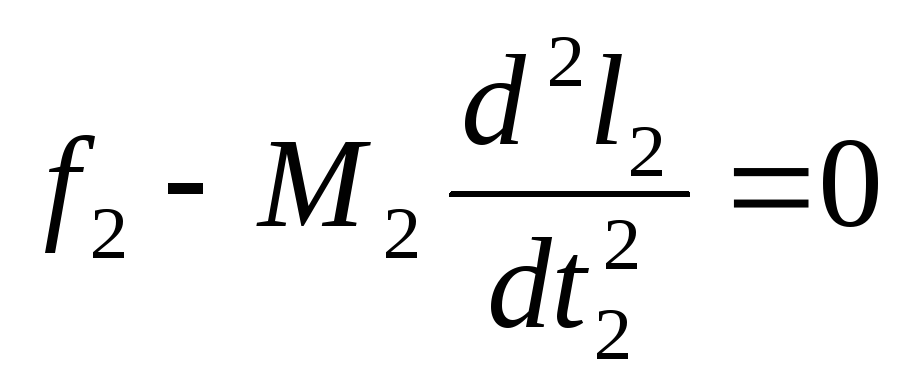
Разделив первое уравнение движения на f1, а второе - соответственно на f2, получим
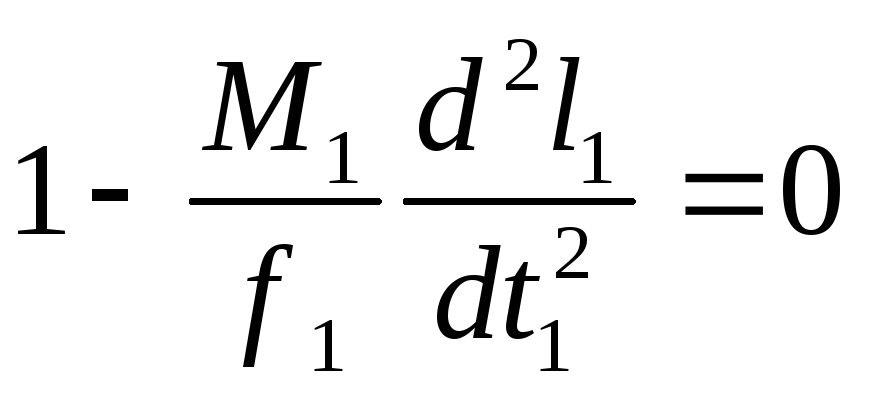
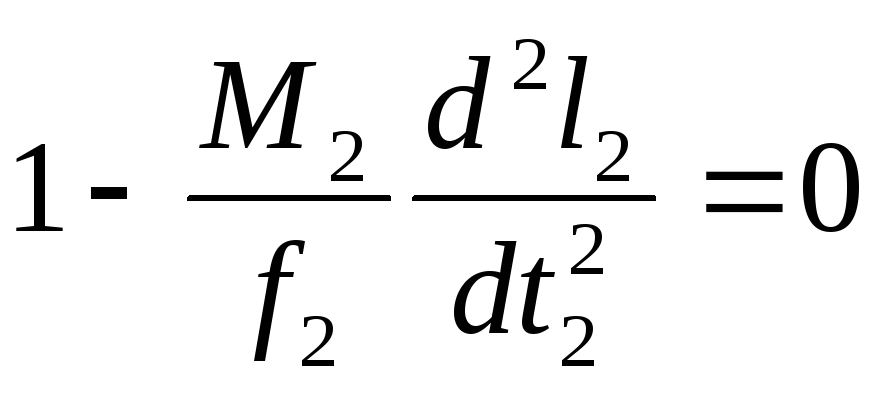 (2.8)
(2.8)
Поскольку явления подобны, то их параметры связаны соотношениями:
M1=mMM2
f1=mff2
l1=mll2
t1=mtt2
Подставив эти соотношения в уравнение (2.8), получим
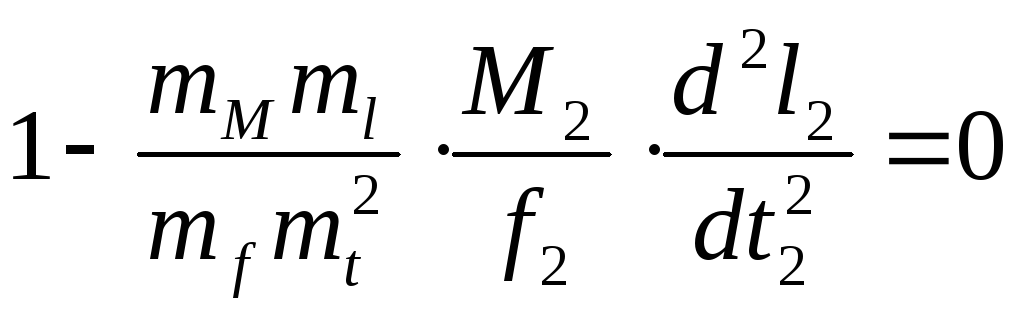
Поскольку уравнение движения первого тела однородное, то
![]() (2.9)
(2.9)
Подставив в (2.9) вместо масштабов отношения сходственных параметров, получим:
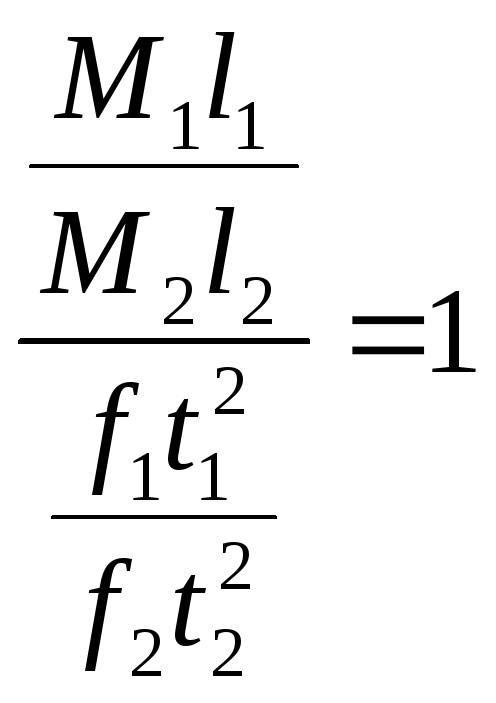 или
или
![]() .
.
Обобщив полученный результат на S подобных систем, получим
![]()
Соотношение
![]() одинаковое для всех подобных систем,
является основным критерием механического
подобия:
одинаковое для всех подобных систем,
является основным критерием механического
подобия:
![]() 1
1
Пример 2.2
Пусть в цепи (рис. 2.3), обладающей сопротивлением R, и индуктивностью L1 при включении ее на постоянное напряжение U1 протекает процесс, описываемый уравнением
![]() (2.10)
(2.10)
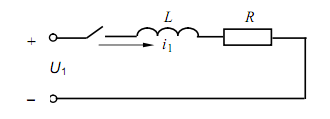
Рис 2.3. Электрическая схема
Во второй цепи с параметрами R2, L2 протекает подобный первому процесс, уравнение которого
![]() (2.11)
(2.11)
Определим критерии подобия и покажем, что они численно одинаковы для обоих процессов.
Разделив (2.10) и
(2.11) соответственно на
![]() и
и![]() ,
получим
,
получим
![]() (2.12)
(2.12)
![]()
Так как процессы подобны, то
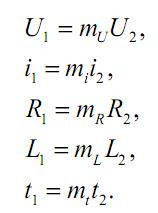 (2.13)
(2.13)
Подставив выражения (2.13) в уравнение (2.12), получим
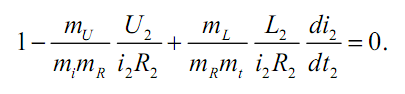
Поскольку уравнение (2.12) однородное, то
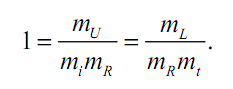
Заменяя в последнем уравнении масштабы отношениями сходственных параметров, получаем
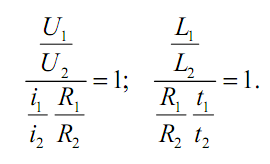
Или в критериальной записи
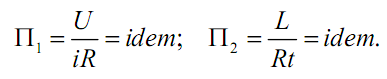
2.4. Применение методов подобия в математическом
моделировании
Теория размерностей и подобия применяется для анализа и упрощения математических моделей. Упрощение состоит в понижении порядка системы уравнений, образующих модель, в уменьшении числа переменных или числа параметров, определяющих процесс. Системы единиц измерений можно выбирать по-разному, причем связи между величинами, определяющими модель, не должны изменяться при изменении единиц измерения.
Инвариантность явлений и процессов к изменению единиц измерения
определяется P -теоремой [11].
Пусть имеется функциональная связь
![]() (2.14)
(2.14)
между n +1 размерными величинами a, a1, …, an , где величины a1, …,ak имеют независимую размерность, и пусть эта связь не зависит от выбора системы единиц измерения (величина a определяемая, а остальные определяющие). Тогда связь (2.14) может быть записана как соотношение
![]() (2.15)
(2.15)
между n +1- k критериями подобия П, П1,…, Пn-k представляющими собой безразмерные комбинации из n +1 размерных величин а, а1, …, аn .
При этом критерии подобия П, П1,…, Пn-k связаны с переменными а, а1, …, аn соотношениями:
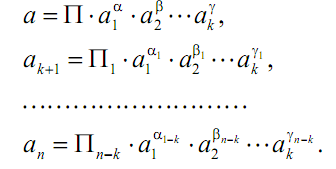 (2.16)
(2.16)
Здесь показатели степеней α, β, …, γ; α1, β1, …, γ1; αn-k , βn-k, …, γn-k те
же, что и в
соответствующих формулах размерностей
для размерно-зависи-мых величин a,
aK+ 1,
an
например в формуле
![]() .
.
Доказательство П - теоремы основано на инвариантности связи (2.14) относительно единиц измерения.
Представим любую размерно-независимую величину ai i = 1, …,k в виде
ai = {ai}[ai],
где {ai} - числовое значение величины ai (безразмерный коэффициент); [ai] - некоторая произвольно выбранная единица измерения.
Числовые значения безразмерных коэффициентов для размерно-зависимых величин a, ak+ 1, an вычисляются с использованием выбранных единиц измерений ai i = 1, …, k по правилу
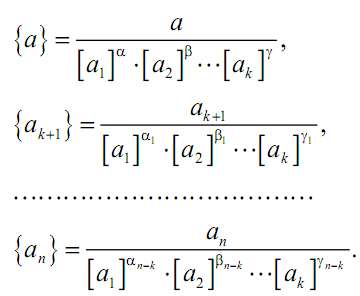
Соотношения (2.14) можно трактовать также и как связь между числовыми значениями величин a, a1, …, an (т.е. связь между безразмерными величинами {a}, {a1}, …., {an}, не зависящую, по предположению, от единиц измерения). Таким образом, для любых единиц измерений [ai] справедливо равенство
![]()
или
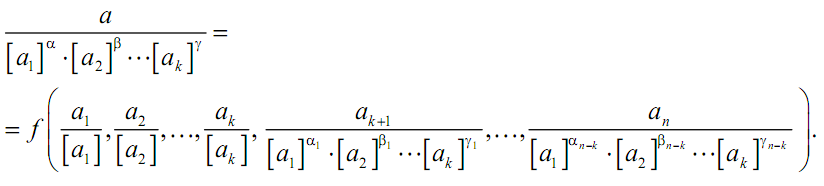
Положим теперь [a1] = a1, [a2] = a2, …, [ak] = ak. Другими словами, выберем единицы измерений так, чтобы в полученной системе единиц измерений величины {a1}, {a2}, …., {ak} тождественно равнялись единице. Тогда из последнего соотношения немедленно вытекают формулы (2.15) и (2.16).
Заметим, что поскольку единицы измерений [a1], [a2], …, [ak] выбраны равными самим величинам a1,a2, …,ak, то эти единицы измерений не остаются постоянными. Каждым новым значениям величин a1,a2, …,ak отвечают новые значения единиц измерений. Однако такой подход к выбору единиц измерений не противоречит законам теории размерностей и подобия.
Применение П -теоремы уменьшает число величин в описании объекта и позволяет явно выразить определяемую величину a , а также величины ak+1,…,an через П, П1, …., Пn-k и a1,a2, …,ak.
В частности, если n = k , то, как следует из уравнения (2.15), П= const и
![]()
т.е. решение задачи получается в виде простого выражения через определяющие параметры. Чтобы знать точное значение a , остается определить константу.
Пример 2.3
Определим с помощью П-теоремы критерий подобия для 2-го закона Ньютона. Этот закон можно записать как функциональную зависимость