ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 31.03.2024
Просмотров: 1113
Скачиваний: 0
СОДЕРЖАНИЕ
Математическое моделирование элементов сложных экологических систем
Лекция 1. Введение в моделирование. Исторический экскурс.
1. Основы моделирования в экологии 1.1. Общие принципы построения моделей в экологии
2.2. Этапы построения математической модели
1.4. Элементы теории подобия, применяемые в моделировании
3.2.2. Выборочный метод в экологометрике.
Зависимость числа интервалов от объема выборки
Статистический ряд по интервалам
Лекция 4. Статистические оценки параметров распределения случайных величин по выборкам
4.4. Статистические оценки гипотез об экологических моделях
Выборка из генеральной совокупности
Статистическая таблица эксперимента
Пример преобразования членов уравнения регрессии
Вычисление данных для линеаризации уравнения регрессии
Нормальные уравнения мнк для некоторых функций
Статистическое оценивание уравнения регрессии и парной корреляции.
Обработка результатов наблюдений
Рекомендации по выбору вида функции
3.4. Динамические статистические модели
Данные по объему сброса качественных сточных вод
Данные по объему сброса сточных вод за 5-летие
Пример расчета 5-летних средних
Расчетные значения для определения уравнения динамики
Ряд динамики для определения сезонных колебаний
Эксперименталъный материал исследования
8.1. Анализ влияния отдельных факторов в экологической модели.
Лекция 9. Методы оптимизации. Метод Лагранжа
Лекция 10. Метод линейного программирования.
Лекция 11. Функциональные модели.
Лекция 12. Модели процессов содержащие обыкновенные дифференциальные уравнения.
Численные ошибки использованных для вычисления данных
Лекция 13. Статистические модели динамики.
Лекция 16. Информационные технологии в экологии. Экологические информационные системы.
1 6.1. Экологические информационные системы
1. Какова область значения для числовых характеристик?
Лекция 17. Использование информационных технологий для решения задач экологии.
Критические значения коэффициента корреляции rk;α
2.1. Подобие физических явлений и его признаки
2.4. Применение методов подобия в математическом
11.3. Численные методы решения дифференциальных уравнений
11.3.2. Процесс численного решения
11.3.4. Модифицированный метод Эйлера
11.3.6. Метод Рунге – Кутта для систем дифференциальных уравнений
11.3.7. Общая характеристика одношаговых методов
11.3.9. Методы прогноза и коррекции
11.3.10. Краткая характеристика методов прогноза и коррекции.
11.3.11. Выбор шага и погрешность решения.
11.4. Имитационное моделирование систем
11.4.1. Принципы имитационного моделирования
11.4.3. Динамическая модель исследуемого объекта
11.4.4. Построение имитационных моделей динамических систем
11.4.5. Преобразование передаточных функций звеньев в дифференциальные уравнения в форме Коши
11.4.6. Синтез имитационной модели на основе структурной схемы
11.5. Теоретические основы построения математических моделей систем
11.5.1. Компонентные и топологические уравнения
11.5.2. Компонентные и топологические уравнения механической системы
11.5.3. Компонентные и топологические уравнения электрической системы
11.5.4. Компонентные и топологические уравнения гидравлической системы
11.5.5. Компонентные и топологические уравнения тепловой системы
11.6.1. Сущность метода электроаналогий.
11.6.2. Электромеханические аналогии
11.6.3. Построение имитационных моделей методом электроаналогий
11.6.4. Плоское прямолинейное движение звеньев
11.6.5. Электрогидравлические аналогии
1. Основы моделирования в экологии 1.1. Общие принципы построения моделей в экологии
Моделирование в научных исследованиях используется практически в любых отраслях национального хозяйства как эффективный инструмент познания того или иного явления, или процесса.
Так как реальный процесс представляет собой, как правило, сложную систему взаимодействия внутренних и внешних частей и факторов, для их изучения исследователи абстрагируются от части взаимодействий и их природы и выделяют те из них, которые в настоящий момент их интересуют. В этом случае принято говорить о модели процесса. Кратко назовем модель процесса, явления или объекта — моделью системы.
Различают по форме представления модели систем: физические, эколого-математические, логические, иконографические и др.
Физические модели — это некоторые реальные системы, в которых реализуются те или иные взаимодействия между элементами и частями изучаемого объекта. Они могут быть полными, частичными и аналоговыми. Полные модели представляют собой объект, измененный в масштабе с возможностью выполнять полностью или частично функции реального объекта. Так, например, при изучении эффективности очистки воды строится опытная очистная станция, ее конструкция представляется в реальном масштабе. Для изучения отдельных частей этой станции могут быть созданы частичные модели, например система обеззараживания воды.
Полные и частичные модели строятся на принципе подобия.
Аналоговые модели строятся на известных аналогиях протекания тех или иных процессов в гидравлике, электротехнике и т.д., с помощью которых можно изучить некоторые экологические процессы в исследуемых системах, например, с помощью создания электрической схемы и ее изучения, полученные результаты, в свою очередь, можно перенести на экологические системы.
Логические модели реальных систем и процессов представля- ют собой описания типа «если..., то...», «если А, то и В...», «если А и В, то С». Они используются в основном для описания процессов, определяющихся качественными параметрами.
Иконографические модели реальных систем представляют собой рисунки, схемы, графики, поясняющие устройство, принцип действия или наглядность тех или иных параметров экологических систем и т.п.
Чаще всего в экологических исследованиях применяются смешанные модели, например логико-математические. Модели этих систем имеют целевое назначение, например, для исследования структуры, функционирования, расхода и т.д.
Модели с т р у к т у р ы предназначены для изучения взаимо- положения и связи элементов системы как внутри нее, так и с внешней средой. Такие модели могут быть представлены в виде схем, сетевых графиков, матриц связи.
Модели ф у н к ц и о н и р о в а н и я предназначены для изучения систем в динамике. Так, модели изменения воздушной среды в течение определенного времени, модели операций при изучении технологических процессов и т.д. Характерным признаком таких моделей в большинстве случаев является изменение параметров системы в функции от времени.
Модели расхода или прибыли используются при определении технико-экономических или иных показателей систем, оптимизации процессов по отдельным критериям.
При изучении экологических процессов и явлений математические модели рассматриваются в тесной связи с целевыми системами и представляют собой некоторые целостные структуры, которые называют эколого-математическими моделями.
Эколого-математические модели — это смешанные модели (логико-математические, математико-иконографические), представляющие определенную совокупность математических зависимостей, логических построений, схем, матриц и т.п., связанных в единую систему, имеющую экологический смысл.
Эколого-математическая модель, например, может быть представлена в виде иконографической модели — схемы модели объекта (рис. 1.1) и в виде функци-ональной зависимости состояния объекта Ф(t) = f(Х, А, G, Y, Q, t), которая является функцией времени от входных факторов состояния объекта, состояния управления, выходных факторов и факторов внешней среды.
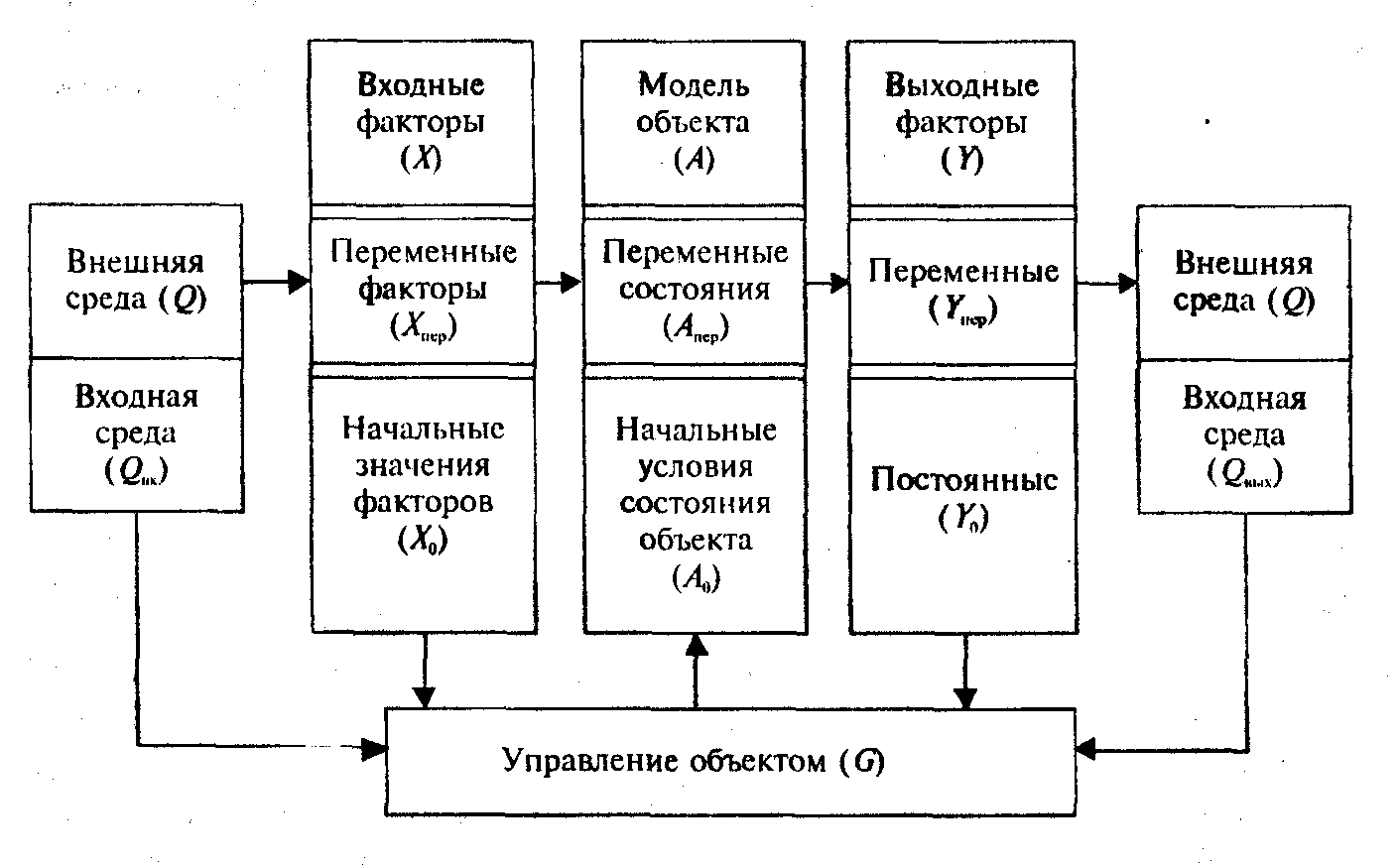
Рис. 1.1. Схема модели объекта
При этом все факторы следует рассматривать в данном случае, в виде векторных вели- чин, изменяющихся с течением времени. При моделировании подобного объекта могут быть применены различного вида модели для исследования тех или иных его частей с различным целевым назначением.
Однако, какие бы модели объектов не строили, в конце концов, мы должны сравнивать их с реальными объектами, что чаще всего возможно в процессе проведения эксперимента (натурного испытания). В экологии встречаются большие трудности, так как ее характеризуют в основном процессы, имеющие значительные продолжительность во времени и трудности воспроизводства эксперимента. Поэтому главным направлением в моделировании экологических процессов является информационное моделирование, создание изоморфных абстрактных имитационных моделей (каждому элементу структуры объекта соответствует один элемент структуры модели), построенных на математическом и логическом аппаратах и реализуемых на ЭВМ.
Главными принципами моделирования экологических объектов являются принципы системности, состоящие из принципов: принципы интегратизма, неопределенности, инвариантности, главных видов деятельности.
Принцип интегратизма заключается в том, что взаимоотношения части и целого характеризуются совокупностью трех эле- ментов:
• первый — возникновение взаимодействующих систем— связей между частями целого;
• второй — утрата некоторых свойств части при вхождении в целое;
• третий — появление новых свойств у целого, обусловленных свойствами составных частей.
При этом обязательна упорядоченность частей, детерминированность их пространственного и функционального взаимоотношений, часть становится компонентом интегрального целого, внутренне объединенного.
Строя модель системы, необходимо исходить из простых условий и шаг за шагом подниматься по восходящим ступеням иерархической градации, переходя к всевозрастающим ступеням усложнения модели. Этот принцип пересекается с известным положением У. Эшби, который рассматривает общую теорию систем как общую теорию упрощения.
Принцип неопределенности предполагает, что «по краям» экологические процессы расплывчаты и неопределенны. Протекая во времени, они постоянно изменяются и, если нам даже удастся установить какое-либо свойство или качество процесса, то оно действительно только в рассматриваемый момент времени и в данной ситуации. Иначе говоря, на микроуровне экологические процессы необходимо изучать с учетом случайно- го изменения факторов.
Принцип неопределенности позволяет также утверждать, что существует уровень факторов, когда их малые отклонения не влекут изменений в состоянии системы. Однако чем сложнее модель системы, чем глубже мы пытаемся анализировать ее, тем неопределеннее становится решение задачи, а ее результаты дальше от практического смысла.
Принцип инвариантности заключается в том, что модель системы должна быть инвариантна для любых регионов, организационных форм производства и изменение каких-либо условий не должно менять существа модели.
Принцип главных видов деятельности состоит в том, что у разных экологических систем существуют «похожие» виды деятельности (управление, регулирование, распределение и т.п.), которые можно выделить как стандартные. Они бывают неизменными на некотором промежутке времени и могут быть описаны некоторыми похожими моделями.
При моделировании объектов и представлении в виде систем необходимо учитывать их общие свойства, например такие, как:
• целостность — устойчивые отношения между элементами системы, при этом состояние любого элемента зависит от состояния всей системы, и наоборот;
• делимость — целостный объект может быть изображен как расчлененный на элементы;
• изолированность — комплекс объектов, образующих систему, связи между ними можно выделить и рассматривать изолированно; изолированность системы относительна, поскольку комплекс объектов, образующих систему, связан с наблюдателем и со средой через некоторые элементы, являющиеся входами и выходами;
• устойчивость — система должна нормально функционировать и быть нечувствительной к неизбежным посторонним возмущающим воздействиям;
• разнообразие — каждый элемент системы обладает собственным поведением и состоянием, отличным от поведения и состояния других составляющих;