ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 31.03.2024
Просмотров: 1046
Скачиваний: 0
СОДЕРЖАНИЕ
Математическое моделирование элементов сложных экологических систем
Лекция 1. Введение в моделирование. Исторический экскурс.
1. Основы моделирования в экологии 1.1. Общие принципы построения моделей в экологии
2.2. Этапы построения математической модели
1.4. Элементы теории подобия, применяемые в моделировании
3.2.2. Выборочный метод в экологометрике.
Зависимость числа интервалов от объема выборки
Статистический ряд по интервалам
Лекция 4. Статистические оценки параметров распределения случайных величин по выборкам
4.4. Статистические оценки гипотез об экологических моделях
Выборка из генеральной совокупности
Статистическая таблица эксперимента
Пример преобразования членов уравнения регрессии
Вычисление данных для линеаризации уравнения регрессии
Нормальные уравнения мнк для некоторых функций
Статистическое оценивание уравнения регрессии и парной корреляции.
Обработка результатов наблюдений
Рекомендации по выбору вида функции
3.4. Динамические статистические модели
Данные по объему сброса качественных сточных вод
Данные по объему сброса сточных вод за 5-летие
Пример расчета 5-летних средних
Расчетные значения для определения уравнения динамики
Ряд динамики для определения сезонных колебаний
Эксперименталъный материал исследования
8.1. Анализ влияния отдельных факторов в экологической модели.
Лекция 9. Методы оптимизации. Метод Лагранжа
Лекция 10. Метод линейного программирования.
Лекция 11. Функциональные модели.
Лекция 12. Модели процессов содержащие обыкновенные дифференциальные уравнения.
Численные ошибки использованных для вычисления данных
Лекция 13. Статистические модели динамики.
Лекция 16. Информационные технологии в экологии. Экологические информационные системы.
1 6.1. Экологические информационные системы
1. Какова область значения для числовых характеристик?
Лекция 17. Использование информационных технологий для решения задач экологии.
Критические значения коэффициента корреляции rk;α
2.1. Подобие физических явлений и его признаки
2.4. Применение методов подобия в математическом
11.3. Численные методы решения дифференциальных уравнений
11.3.2. Процесс численного решения
11.3.4. Модифицированный метод Эйлера
11.3.6. Метод Рунге – Кутта для систем дифференциальных уравнений
11.3.7. Общая характеристика одношаговых методов
11.3.9. Методы прогноза и коррекции
11.3.10. Краткая характеристика методов прогноза и коррекции.
11.3.11. Выбор шага и погрешность решения.
11.4. Имитационное моделирование систем
11.4.1. Принципы имитационного моделирования
11.4.3. Динамическая модель исследуемого объекта
11.4.4. Построение имитационных моделей динамических систем
11.4.5. Преобразование передаточных функций звеньев в дифференциальные уравнения в форме Коши
11.4.6. Синтез имитационной модели на основе структурной схемы
11.5. Теоретические основы построения математических моделей систем
11.5.1. Компонентные и топологические уравнения
11.5.2. Компонентные и топологические уравнения механической системы
11.5.3. Компонентные и топологические уравнения электрической системы
11.5.4. Компонентные и топологические уравнения гидравлической системы
11.5.5. Компонентные и топологические уравнения тепловой системы
11.6.1. Сущность метода электроаналогий.
11.6.2. Электромеханические аналогии
11.6.3. Построение имитационных моделей методом электроаналогий
11.6.4. Плоское прямолинейное движение звеньев
11.6.5. Электрогидравлические аналогии
8.1. Анализ влияния отдельных факторов в экологической модели.
В экологии часто встречаются объекты исследования, состояние которых определяется факторами, не имеющими количественной оценки. Такими факторами могут быть неуправляемые и управляемые переменные, которые по каким-либо причинам не позволяют производить их измерение в данном эксперименте, а также те не- контролируемые переменные, уровни варьирования которых можно произвольно выбирать и фиксировать по времени.
Для изучения влияния факторов подобного рода на функцию отклика Y (целевую функцию), их общего оценивания, ранжирования и выделения среди них существенных, методы регрессионного анализа непригодны, поскольку они решают задачи определения вида математической модели при варьировании величиной факторов. Здесь целесообразно использовать методы дисперсионного анализа.
назад
Лекция 9. Методы оптимизации. Метод Лагранжа
9.1. Метод Лагранжа.
Оптимизация играет важную роль при экологических исследованиях и поиске наилучших характеристик объекта или наименьших затрат ресурсов.
Оптимизации подвергается целевая функция, которая в этом случае выражается через какие-либо параметры (факторы), при не- которых заданных ограничениях. В общем случае задача оптимизации формулируется следующим образом: найти значения параметров х1, х2, ..., хn, при которых целевая функция
Y=f(х1, х2, ..., хn)
принимает максимальное (минимальное) значение при функциональных ограничениях, выражаемых в виде равенств
F1=f1(х1, х2, ..., хn)
F2=f2(х1, х2, ..., хn) (9.1)
………………………..
Fm=fm(х1, х2, ..., хn)
и областных ограничений в виде неравенств
Ф1=φ1(х1, х2, ..., хn) ≤ b1 Ф2=φ2(х1, х2, ..., хn) ≤ b2
……………………… (9.2)
Фp=φp(х1, х2, ..., хn) ≤ bp
Для решения таких задач могут быть использованы методы: диффуренциро-ваия, множителей Лагранжа, численные методы, математическое программирование и др.
При оптимизации методом дифференцирования оптимум находится приравниванием частных производных целевой функции и затем из решений совместной системы n-уравнений находится значение всех переменных хi.
i=![]()
Пример. Стоимость продукта зависит от степени его очистки х, ма- териалов на очистку k1 и затрат труда k2 что выражается зависимостью
![]()
При
этом
чистота
продукта
(х)
изменяется
в
пределах
от
25%
до
90%,
а
имеющиеся средства
на
очистку
равны
![]() ,
где
,
где![]() —
максимальная
сумма
денежных
средств.
—
максимальная
сумма
денежных
средств.
Требуется найти такое значение х, при котором затраты С ми- нимальны.
Р е ш е н и е. Находим производную
![]()
![]()
Откуда
![]() .
.
Это
оптимальное
значение
получено
без
учета
ограничений
25%
<
х
<
90%
и
![]() .Если
они
при
этом
удовлетворяются,
то
обычно
решение
находится
путем использования
в
качестве
ограничения
соответствующего
предельно
допустимого значения,
т.е.
для
нашего
примера
нижнего
(25%-ного)
или
верхнего(90%-ного) уровня.
При
наличии
функциональных
ограничений
их
обычно можно
использовать
до
начала
дифференцирования
для
уменьшения
числа
параметров
и,
таким
образом,
основная
задача
не
меняется.
.Если
они
при
этом
удовлетворяются,
то
обычно
решение
находится
путем использования
в
качестве
ограничения
соответствующего
предельно
допустимого значения,
т.е.
для
нашего
примера
нижнего
(25%-ного)
или
верхнего(90%-ного) уровня.
При
наличии
функциональных
ограничений
их
обычно можно
использовать
до
начала
дифференцирования
для
уменьшения
числа
параметров
и,
таким
образом,
основная
задача
не
меняется.
Метод множителей Лагранжа используется, когда целевая функция находится при функциональных ограничениях. Задача решается следующим образом.
Оптимизировать целевую функцию
Y= f(х1, х2, ..., хn) (9.3)
при ограничениях
Ф1= φ1(х1, х2, ..., хn) = 0
Ф2= φ2(х1, х2, ..., хn) = 0
………………………. (9.4)
Фm= φm(х1, х2, ..., хn) = 0.
Дифференцируя целевую функцию, найдем ее дифференциал и приравняем его к нулю
![]()
Дифференцируем каждые т ограничений
![]()
![]()
……………………..
![]()
Умножаем
каждое
из
т
уравнений
(9.4)
на
неизвестный
параметр
λi,
i=![]() ,
называемый
множителем
Лагранжа.
Эти
множители
различны
для
разных
уравнений.
,
называемый
множителем
Лагранжа.
Эти
множители
различны
для
разных
уравнений.
Имеем
![]()
![]()
![]()
……………………
![]()
![]()
Если теперь сложить вместе все эти уравнения, прибавив уравнение dY, то получим:
![]()
или
![]()
Поскольку все параметры хi независимы, чтобы это уравнение удовлетворялось, каждый из n заключенных в скобки членов предыдущего уравнения должен равняться нулю. Отсюда получим n уравнений вида:
![]() i=
i=![]()
Имеется
также
m уравнений.
Таким
образом,
имеется
всего
(n
+
m)
уравнений с
(n
+ m)
неизвестными:
n
неизвестных
хi,
и
т
неиз-
вестных
![]() .
Решение этой
системы
даст
искомое
оптимальное
реш
ение.
.
Решение этой
системы
даст
искомое
оптимальное
реш
ение.
Пример. Требуется построить цилиндрический резервуар емкостью 10м3 при наименьшем расходе материала. Таким образом, целевой функцией является площадь поверхности А= 2πr2+ 2 πrl, где r — радиус цилиндра; l — высота цилиндра. Функциональное ограничение V= πr2l = 10м3.
Р е ш е н и е. Находим производные
![]()
![]()
Уравнение
ограничения
![]() :
:
![]()
![]()
Отсюда получим три уравнения
![]() ,
,
![]()
![]()
определяющих
три
неизвестных
r,
l
и
![]() ,
т.е.
,
т.е.
4πr+2πl+λ(-2πl)=0;
-2πr+ λ(πr2)=0;
V= -πr2l =0
Решая уравнения, получим:
λ
=![]() l=2r;
r=
l=2r;
r=![]()
при V= 10м3; r = 1,167м; l = 2,334м.
назад
Лекция 10. Метод линейного программирования.
Методы математического программирования составляют раздел математики, в котором изучаются методы нахождения минимума или максимума функции конечного числа переменных при условии, что переменные удовлетворяют конечному числу дополнительных условий (ограничений), имеющих вид уравнений или неравенств. Различают линейное и нелинейное математическое программирование. Рассмотрим элементы линейного программирования (ЛП).
Линейным программированием называется раздел математики, в котором изучаются методы нахождения минимума или максимума линейной функции конечного числа переменных при условии, что переменные удовлетворяют конечному числу дополнительных ограничений, имеющих вид линейных уравнений или неравенств. Таким образом, задача линейного программирования (ЗЛП) в общем случае формулируется следующим образом: найти такие значения действительных переменных х1, х2 ..., хm для которых целевая функция
Q(x) = р1х1 + р2 х2 + ... + рnхn (10.1) (5.5)
принимает минимальное значение на множестве точек, координаты которых удовлетворяют условиям
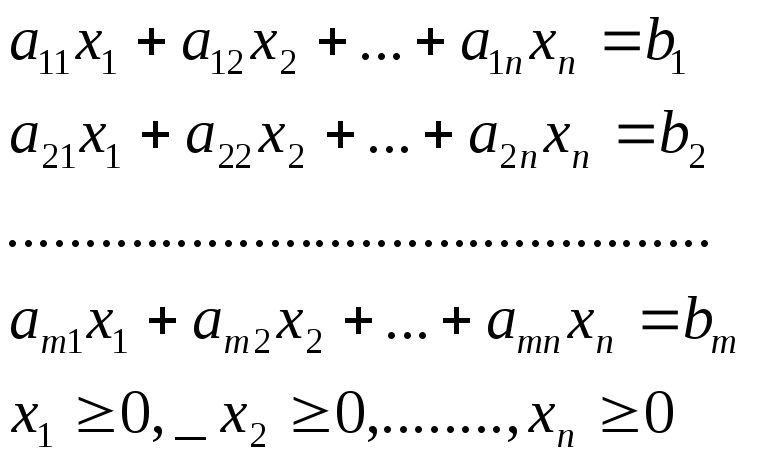 (10.2)
(5.6)
(10.2)
(5.6)
где коэффициенты аij, bj, рj, (i =1, j =1,n) — действительные числа.
Можно предполагать, что
b1≥0, b2≥0, ..., bn ≥0.
В матричном виде ЗЛП формулируется
АХ= b; х ≥0; Qmin(х) ≥ рrх,
где х
=(х1,
х2,
...,
xn)T
![]() Rn,
А
—
матрица
Rn,
А
—
матрица
![]() размера
тn;
размера
тn;