Файл: Математическое моделирование в экологии.doc

Таким образом, разность |Θ_b – Θ| будет сколь угодно малой, а предел стремится к единице при увеличении объема выборки при >0. Свойство очевидно, так как чем ближе n к ∞, тем ближе оценка Θ_b к Θ. Отсюда следует, что состоятельность оценки возрастает с увеличением объема выборки.

Выборочная несмещенная оценка называется эффективной, если она имеет минимальную дисперсию по сравнению с другими возможными оценками. Так, например, имеются две выборочные оценки Θ_b1 и Θ_b2 с дисперсиями D(Θ_b1) > D(Θ_b2), тогда эффективной будет оценка Θ_b2. Достаточной называют выборочную оценку, если она включает всю информацию, которая содержится в выборке относительно определенного параметра. Если, например, по выборке (х₁, х₂, ..., х_n) производится оценка неизвестной вероятности Р, то вполне достаточно знать сумму варианта 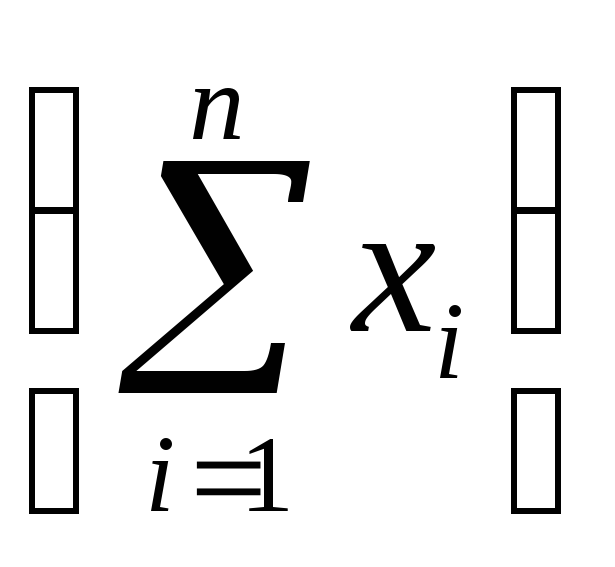, т.е. общее число случаев, благоприятствующих данному событию. Отдельные же значения х_i уже не содержат никакой новой информации и ничего не поясняют относительно значений Р. Выборочные оценки могут быть точечными и интервальными.

Точечные оценки — это оценки некоторых неизвестных числовых параметров распределения случайных величин. Они представляют собой числа, полученные путем подстановки выборочных значений

х₁, х₂, ..., х_n, в формулу для оценивания искомого параметра. Точечные оценки параметров Θ _b не дают информации о степени близости к соответствующему теоретическому параметру генеральной совокупности Θ. Поэтому более информативный способ оценивания неизвестных параметров состоит в построении интервала, в котором оказывается оцениваемый параметр.

Интервальной оценкой параметра Θ называется интервал, гра- ницы которого Θ _b1 и Θ _b2 являются функциями выборочных значе- ний х₁,х₂,...,х_n, и который с заданной вероятностью накрывает оцениваемый параметр Θ

Р{ Θ _b1 < Θ < Θ _b2} = .

Величина называется доверительной вероятностью или надежностью, с которой оценка Θ заключается в интервал (Θ _b1 и Θ _b2), она записывается в виде = 1 - α, где α — уровень значимости, определяющий величину вероятности того, что оценка Θ выйдет за пределы интервала Θ _b1 и Θ _b2.

Ширина доверительного интервала равна Н = Θ _b1 - Θ _b2.

Точечные оценки параметров распределения случайных величин. Основными методами получения точечных оценок являются метод моментов, метод наименьших квадратов (МНК) и метод максимально- го правдоподобия (ММП).

Метод моментов является наиболее простым и общим способом точечной оценки. Пусть имеется выборка (х₁, х₂, ..., х_n) случайной величины Х. Среднее значение наблюдаемого признака можно оп- ределить по формуле

Таким образом, представляет собой эмпирическое, или выборочное среднее. Если вычислено среднее, то легко найти отклонение каждого наблюдения δ, от среднего δ_i = х_i — .

Величину S² =называют дисперсией или вторым центральным моментом эмпирического распределения

m₂ = S²

В случае одномерного эмпирического распределения произволь- ным моментом порядка К называется сумма К-тых степеней отклоне- ний результатов наблюдений от произвольного числа С, деленная на объем выборки n

где k может принимать любые значения натурального ряда чисел. Начальным моментом первого порядка является выборочное среднее , т.е.

что мы видели ранее. Если С = , то имеем центральные моменты

…………………

Среднеквадратическое отклонение равно

Выборочное значение коэффициента вариации V, являющееся мерой относительной изменчивости наблюдаемой случайной вели- чины, вычисляют по формуле

или в процентах

Если известна форма связи искомого параметра с моментами, то вначале находят выборочные оценки моментов, а затем, используя форму связи, вычисляют оценку самого параметра. Например, в качестве меры симметричности графика распределения случайных величин, используется коэффициент асимметрии А_s который для симметричного распределения равен нулю. Для оценки асимметричности используется формула

Если А_s > 0, то график плотности вероятности имеет «скос» с левой стороны от , а если А_s < 0, то — с правой.

В качестве меры «крутости» графиков распределения случайных величин используют коэффициент эксцесса E_k, характеризующий «крутость» графика по сравнению с кривой Гаусса. Для оценки Е, используется формула

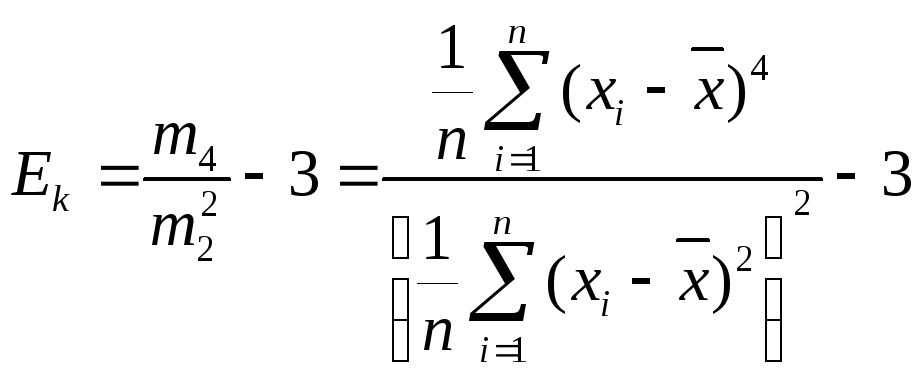
Если E_k ≥ 0, то кривая островершинная, при E_k < 0 — плоско- вершинная (пологая). Метод моментов, как правило, приводит к состоятельным оценкам. Однако при малых выборках оценки мо- гут оказаться значительно смещенными и малоэффективными. Метод моментов достаточно эффективен для оценки параметров нормально распределенных случайных величин.

Метод наименьших квадратов в основном используется для оценки коэффициентов уравнения регрессии, например в ального параметра используется процентная частота, то ее ошибка вычисляется по формуле00

и будет рассмотрен в регрессионном анализе.

Метод максимального правдоподобия имеет большое преимущество по сравнению с другими методами точечной оценки. Он дает состоятельные, распределенные асимптотически нормально, эффективные оценки. Хотя эти оценки могут быть несколько смещенными.

Метод состоит в следующем. Пусть имеется выборка (х₁, х₂, ..., х_n), а рассматриваемый признак х имеет распределение плотности веро- ятностей f(x, Θ), где Θ есть неизвестный параметр, который требу- ется оценить по выборке. В силу случайности попадания в выборку величины х_i. вероятность осуществления данной выборки равна произведению плотности вероятностей

Такая функция называется функцией правдоподобия выборки и обозначается через L, т.е.

Выборочная оценка, которая обращает в максимум функцию правдоподобия, называется оценкой максимума правдоподобия.

Для нахождения максимума определяем частную производную и приравниваем ее к нулю,

Например, для показательного распределения f(x, Θ)= Θе^Θx, где Θ — неизвестный параметр, который следует оценить по выборке (x₁,х₂,...,х_n), составим функцию правдоподобия

Прологарифмируем функцию L

Теперь ее продифференцируем и приравняем к нулю

Отсюда

Для оценки величины рассеивания средних выборочных относительно математического ожидания генеральной совокупности в случае нормального распределения случайной величины х можно применить формулу

где D(x) — известная дисперсия генеральной совокупности;

n — объем выборки.

Средняя ошибка выборочной средней

Несмещенная оценка дисперсии, получается, по методу максимального подобия с поправкой

Характеристика рассеивания дисперсии S определяется по формуле

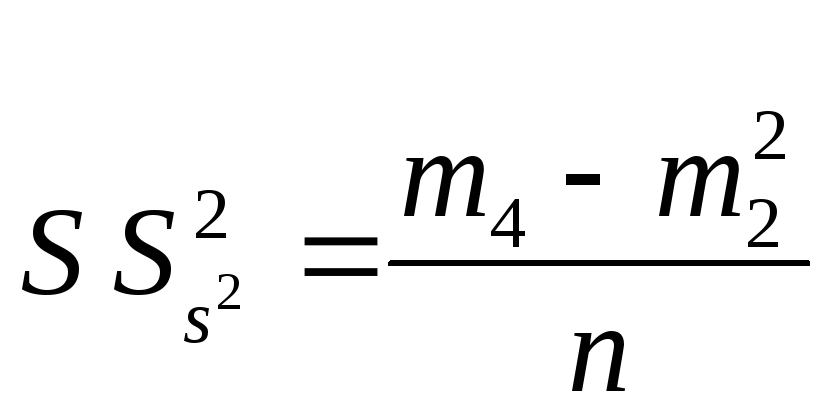
Средняя ошибка выборочной дисперсии

Для нормального распределения

При обработке статистических данных используют следующие виды оценок:

1. Средняя арифметическая для объема выборки n

При разделении выборки на k групп, в которых x_j встречается m_j раз

Средняя арифметическая в группе k

Средняя групповая

4.2. Средняя геометрическая используется тогда, когда вариант х_i имеет размерность нулевого порядка. Величины такой размерности выражают вторичные признаки, являющиеся отношением двух одноименных величин, например измеренная в результате опыта величина сравнивается с некоторым стандартным значением. В результате получается, что величина х_i является безразмерной. Тогда средняя геометрическая равна

или

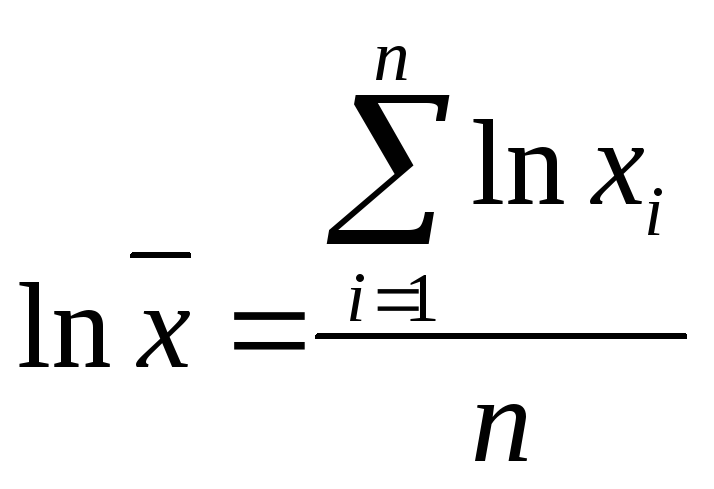
4.3. Средняя гармоническая имеет свойство усреднять при неизменной сумме величин, обратных усредняемым. Она применяется тогда, когда варианта х_i представлена обратной величиной и определяется по формуле