Файл: Математическое моделирование в экологии.doc

схему замещения. Прямоугольники с обозначениями напряжений R_a и R_b рассматриваем теперь как две части электрического биполярного разъема (рис.6.16), причем направления стрелок внутри прямоугольников соответствуют полярности э.д.с. на контактах разъема.

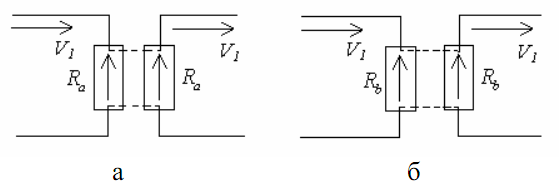
Рис.6.16. Соединения подсистем:

а – первой со второй; б – второй с третьей

Непосредственно из схем разъемных соединений следуют очевидные правила:

1. токи, протекающие через две одноименные части разъема равны между собой по модулю;

2. направления токов, протекающих через две одноименные части разъема, противоположны по отношению к э.д.с. на контактах разъема. Это означает, что если в правой части разъема ток «втекает в стрелку», то в левой части разъема он вытекает из «стрелки», и наоборот (рис.6.16).

Общая электрическая схема замещения (рис 6.17) содержит четыре контура и четыре трансформатора.

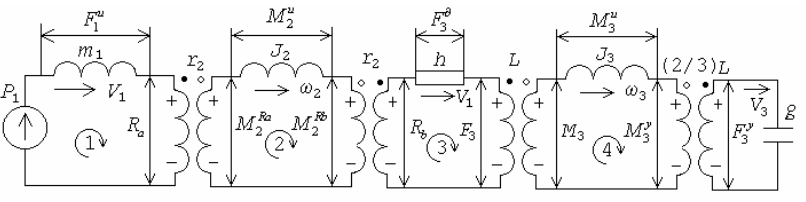
Рис. 6.17. Общая электрическая схема замещения

Уравнения Кирхгофа для контуров 1-4 совпадают с уравнениями сил и моментов (6.4–6.6). Записываем уравнения трансформаторов, куда включаем соотношения напряжений, токов и скоростей изменений токов.

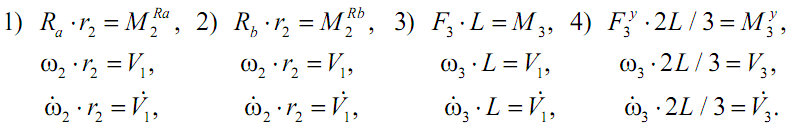
Компонентные уравнения инерционных, диссипативных и упругих элементов:

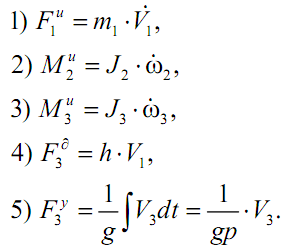
Далее строим сеть связей физических величин (рис. 6.18). Эту работу следует выполнять, соблюдая следующие правила:

1. В уравнениях Кирхгофа для контуров можно выносить вправо от знака равенства только напряжения на индуктивностях и на активных сопротивлениях, а также напряжения, соответствующие неизвестным внутренним силам или моментам. Напряжения на емкостях выносить вправо от знака равенства нельзя.

2. Если инерционное звено соединено с другими звеньями упругими связями, то в уравнении Кирхгофа напряжение на индуктивности, эквивалентной рассматриваемому инерционному звену, всегда выносят вправо от знака равенства.

3. Если два или более инерционных звена соединены жесткой кинематической связью, то из этой группы звеньев надо выбрать одно ведущее звено. Соответственно в уравнениях Кирхгофа надо вынести вправо от знака равенства только то напряжение, которое эквивалентно инерционной силе на ведущем звене.

Напряжения на остальных инерционных звеньях рассматриваемой группы выносить вправо от знака равенства нельзя.

4. Чтобы определить напряжение на конденсаторе, надо знать протекающий через него ток.

5. Напряжение на активном сопротивлении можно определить с помощью тока, протекающего через это сопротивление, или из уравнения Кирхгофа для соответствующего контура.

6. Напряжение на индуктивности можно определить с помощью уравнения Кирхгофа для контура, содержащего эту индуктивность, или с помощью производной от тока через индуктивность.

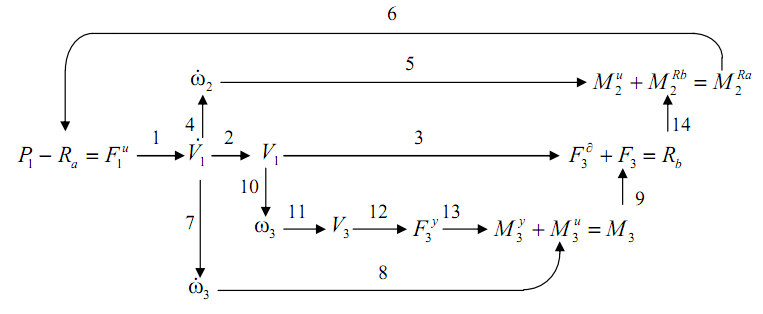
Рис. 6.18. Сеть связей

Таблица 6.5

Передаточные функции элементарных звеньев

Чтобы перейти от сети связей к структурной схеме динамической системы, записываем передаточные функции элементарных звеньев (табл. 6.5) и заменяем в сети связей ветви на передаточные функции этих звеньев.

Общая структурная схема (рис.6.19) содержит два интегрирующих звена.

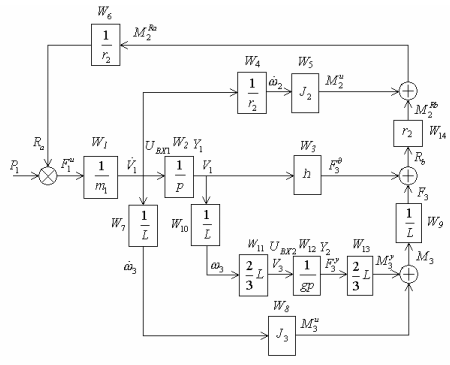
Рис. 6.19. Общая структурная схема

Дифференциальные уравнения этих звеньев имеют следующий вид:

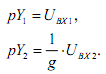
Записываем уравнение связи для первого интегрирующего звена.

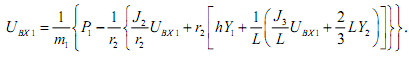
Раскрывая скобки и решая данное уравнение относительно U_BX1, получаем:

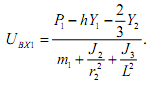
Уравнение связи для второго интегрирующего звена имеет следующий вид:

Подставляя выражения BX1 U и BX 2 U в дифференциальные уравнения интегрирующих звеньев и полагая

получаем общую систему дифференциальных уравнений математической модели в форме Коши:

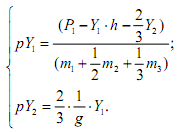
11.6.4. Плоское прямолинейное движение звеньев

Пример 6.3

В качестве первого примера возьмём диск радиуса r, катящийся по плоской поверхности под действием внешней силы T, приложенной к центру диска (рис. 6.20).

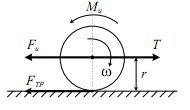
Рис. 6.20

Под действием силы T тело вращается по часовой стрелке со скоростью ω. Силами сопротивления здесь являются инерционная сила F_и и сила трения F_ТР. Составим уравнение равновесия указанных выше сил:

(6.7)

и уравнение действующих на тело моментов:

(6.8)

где .

Уравнения (6.7-6.8) служат основой для построения эквивалентной электрической схемы (рис. 6.21). Эта схема строится в два этапа. Вначале следует вычертить нижний контур, в котором напряжения и э.д.с. должны соответствовать уравнению равновесия сил (6.7). На втором этапе чертим верхний контур, отвечающий

уравнению равновесия моментов (6.8). Заметим, что в уравнении (6.8) момент трения M_TP определяется в виде произведения силы трения F_TP на радиус r . Чтобы выполнить операцию умножения, в электрическую схему введен трансформатор с коэффициентом трансформации r .

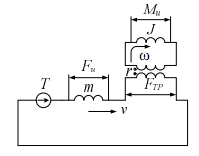
Рис. 6.21

Уравнения трансформатора включают соотношения для напряжений, токов и скоростей изменений токов:

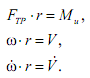
Далее приступаем к построению сети связей физических величин. Для этого в уравнении (6.7) выносим вправо инерционную составляющую F_u (см. па-раф 6.2). Сеть связей состоит из шести ветвей (рис.6.22).

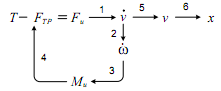
Рис.6.22

С помощью сети связей определяем передаточные функции элементарных звеньев (табл. 6.6).

Таблица 6.6

Передаточные функции элементарных звеньев

Дальнейший переход от сети связей к структурной схеме динамической системы осуществляется так же, как в предыдущем примере.

Пример 6.4

В качестве второго примера возьмём тот же диск радиуса r, катящийся по плоской поверхности под действием внешней силы T приложенной к верхней точке диска (рис.6.23). Под действием силы T, тело вращается по часовой стрелке со скоростью ω. Силами сопротивления здесь являются инерционная сила F_u и сила трения F_ТР. Составим уравнение равновесия указанных выше сил.

(6.9)

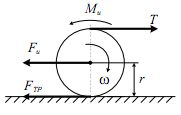
Рис. 6.23

Составим уравнение равновесия действующих на тело моментов. Моменты определяем относительно центра масс тела.

(6.10)

где ,.

Уравнения (6.9) и (6.10) служат основой для построения эквивалентной электрической схемы (рис. 6.24). Переменные M_TP и M_T, входящие в уравнение (6.10), определяются произведениями соответствующих сил F_TP и T на радиус r. Чтобы выполнить указанные операции умножения, в электрической схеме применены два трансформатора с коэффициентом передачи r.

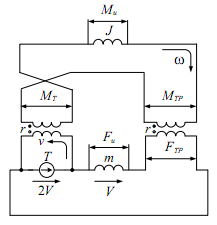
Рис. 6.24

Записываем уравнения трансформаторов:

Чтобы построить сеть связей, воспользуемся уравнением (6.9).

Рис.6.25

В этом уравнении вынесем вправо инерционную составляющую F_u и полученную зависимость поместим в сеть связей (рис.6.25). Сеть связей состоит из 7 ветвей.

Каждой ветви построенной сети связей отвечает элементарное звено. Сводим передаточные функции элементарных звеньев в общую таблицу (табл.6.7). Дальнейший переход от сети связей к структурной схеме динамической системы осуществляется так же, как в примере 1.

Пример 6.5

В качестве следующего примера возьмём диск, подвешенный на нити, один конец которой закреплён на неподвижном основании, а к другому концу приложено некоторое внешнее воздействие Т₁, причём Т₁ > P/2 > Т₂ (рис. 6.26). Диск имеет радиус r. Внешняя сила T₁ создаёт вращающий момент М_Т1, под действием которого диск вращается по часовой стрелке с угловой скоростью ω. Инерционный момент M_и и момент М_Т2, создаваемый силой натяжения нити T₂, препятствуют вращению

диска и, следовательно, являются силами сопротивления.

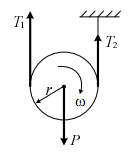
Рис. 6.26

Таблица 6.7

Передаточные функции элементарных звеньев

Составим уравнение равновесия сил

(6.11)

и уравнение равновесия моментов

(6.12)

где ,

Уравнения (6.11) и (6.12) служат основой для построения эквивалентной электрической схемы (рис.6.27).

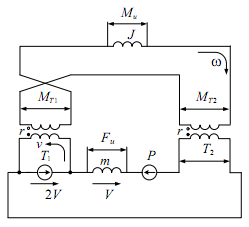
Рис. 6.27

Уравнения трансформаторов:

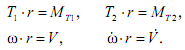
В качестве основы для построения сети связей (рис.6.28) использовано уравнение (6.11). Передаточные функции в табл. 6.8.

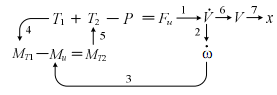
Рис. 6.28

Таблица 6.8

Передаточные функции элементарных звеньев

Пример 6.6

В качестве следующего примера рассмотрим механическое устройство, которое представляет собой жёсткий вал на 3 опорах, обладающих свойствами упругости и демпфирования (рис.6.29). Такое устройство может служить прототипом шпинделя металлорежущего станка, установленного на 3 подшипниках.

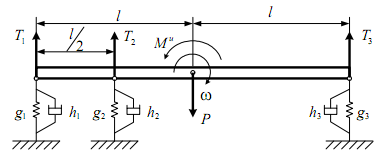
Рис. 6.29

В рассматриваемом примере вал длинной 2l под действием внешней силы P и сил реакций Т₁, Т₂, Т₃ в опорах совершает сложные колебания, которые можно представить как сумму поступательных движений вала параллельно самому себе и вращательных движений вала, совершаемых вокруг его центра масс. Внутренние силы Т₁, Т₂, Т₃ в опорах зависят от значений коэффициентов податливости g₁, g₂, g₃ и коэффициентов демпфирования h₁, h₂, h₃ опор.