ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 31.03.2024
Просмотров: 1061
Скачиваний: 0
СОДЕРЖАНИЕ
Математическое моделирование элементов сложных экологических систем
Лекция 1. Введение в моделирование. Исторический экскурс.
1. Основы моделирования в экологии 1.1. Общие принципы построения моделей в экологии
2.2. Этапы построения математической модели
1.4. Элементы теории подобия, применяемые в моделировании
3.2.2. Выборочный метод в экологометрике.
Зависимость числа интервалов от объема выборки
Статистический ряд по интервалам
Лекция 4. Статистические оценки параметров распределения случайных величин по выборкам
4.4. Статистические оценки гипотез об экологических моделях
Выборка из генеральной совокупности
Статистическая таблица эксперимента
Пример преобразования членов уравнения регрессии
Вычисление данных для линеаризации уравнения регрессии
Нормальные уравнения мнк для некоторых функций
Статистическое оценивание уравнения регрессии и парной корреляции.
Обработка результатов наблюдений
Рекомендации по выбору вида функции
3.4. Динамические статистические модели
Данные по объему сброса качественных сточных вод
Данные по объему сброса сточных вод за 5-летие
Пример расчета 5-летних средних
Расчетные значения для определения уравнения динамики
Ряд динамики для определения сезонных колебаний
Эксперименталъный материал исследования
8.1. Анализ влияния отдельных факторов в экологической модели.
Лекция 9. Методы оптимизации. Метод Лагранжа
Лекция 10. Метод линейного программирования.
Лекция 11. Функциональные модели.
Лекция 12. Модели процессов содержащие обыкновенные дифференциальные уравнения.
Численные ошибки использованных для вычисления данных
Лекция 13. Статистические модели динамики.
Лекция 16. Информационные технологии в экологии. Экологические информационные системы.
1 6.1. Экологические информационные системы
1. Какова область значения для числовых характеристик?
Лекция 17. Использование информационных технологий для решения задач экологии.
Критические значения коэффициента корреляции rk;α
2.1. Подобие физических явлений и его признаки
2.4. Применение методов подобия в математическом
11.3. Численные методы решения дифференциальных уравнений
11.3.2. Процесс численного решения
11.3.4. Модифицированный метод Эйлера
11.3.6. Метод Рунге – Кутта для систем дифференциальных уравнений
11.3.7. Общая характеристика одношаговых методов
11.3.9. Методы прогноза и коррекции
11.3.10. Краткая характеристика методов прогноза и коррекции.
11.3.11. Выбор шага и погрешность решения.
11.4. Имитационное моделирование систем
11.4.1. Принципы имитационного моделирования
11.4.3. Динамическая модель исследуемого объекта
11.4.4. Построение имитационных моделей динамических систем
11.4.5. Преобразование передаточных функций звеньев в дифференциальные уравнения в форме Коши
11.4.6. Синтез имитационной модели на основе структурной схемы
11.5. Теоретические основы построения математических моделей систем
11.5.1. Компонентные и топологические уравнения
11.5.2. Компонентные и топологические уравнения механической системы
11.5.3. Компонентные и топологические уравнения электрической системы
11.5.4. Компонентные и топологические уравнения гидравлической системы
11.5.5. Компонентные и топологические уравнения тепловой системы
11.6.1. Сущность метода электроаналогий.
11.6.2. Электромеханические аналогии
11.6.3. Построение имитационных моделей методом электроаналогий
11.6.4. Плоское прямолинейное движение звеньев
11.6.5. Электрогидравлические аналогии
Технологии в системе ГИС используются практически во всех сферах хозяйства страны и незаменимы в случаях, где требуются пространственно-координатные данные объекта или данные для построения информационной модели территории.
Модель формируется послойно, где каждый информационный слой объединяет группу объектов одного типа (например, леса, реки, озера, здания, сооружения и т.п.). Однотипные объекты описаны словами, цифрами, формулами и формируют так называемые атрибутивные данные слоя.
Принципиальным моментом является то, что создаваемые и существующие информационные слои привязываются к единой пространственной основе, т.е. формируются в рамках единой картографической системы.
Отличительной особенностью начального этапа развития технического обеспечения ГИС является ориентация на территориальные вычислительные комплексы. Необходимо найти возможности для интеграции в них, что предполагает методическое и информационно-- программное единство методов и моделей реализации однотипных функций управления на различных уровнях системы.
При этом при разработке эколого-математических моделей должно быть обеспечено согласование системы критериев и ограничений, а также единство методов, средств агрегирования и дезагрегирования необходимой информации.
В современных условиях создание ГИС реализуется на новых принципах в виде межведомственного территориально-распределительного вычислительного комплекса коллективного пользования (МТВК).
Основные цели создания МТВК:
• оперативность и качество обслуживания пользователей за счет децентрализованных методов обработки данных, использования на всех уровнях управления локальных вычислительных устройств для первичной обработки экологической информации в местах ее возникновения;
• повышение эффективности использования вычислительной техники за счет концентрации вычислительных ресурсов в центрах обработки данных, возможности оперативного распределения и перераспределения свободных вычислительных мощностей, специализации отдельных вычислительных центров по сопровождению (эксплуатации) проблемно-ориентированных функциональных программных комплексов, унификации технологии обработки данных;
• оперативность решения межведомственных задач управления и информационного обслуживания пользователей за счет комплексирования средств вычислительной техники различных предприятий и организаций.
Требования адекватности построения генеральной схемы управления ГИС определяют выделение следующих уровней организации комплекса:
• вычислительную сеть для обслуживания экологических организаций;
• ведомственную (отраслевую) вычислительную сеть; • межведомственную вычислительную сеть.
Взаимодействие между уровнями связано с обменом информацией при решении функциональных задач ГИС и осуществляется на уровне обмена информацией через внешние носители и по выделенным каналам связи. При этом технология взаимодействия определяется системой территориальных стандартов.
В системе ГИС в качестве оконечных вычислительных устройств целесообразно использовать проблемно-ориентированные автоматизированные места (АРМ).
Одной из подсистем ГИС должна быть экспертная система, как часть искусственного интеллекта. Она включает базу данных с на- бором правил и механизмом вывода, позволяющим на основе представляемых фактов распознать экологическую ситуацию, поставить диагноз, формулировать решения или дать рекомендации персоналу для выбора плана действий.
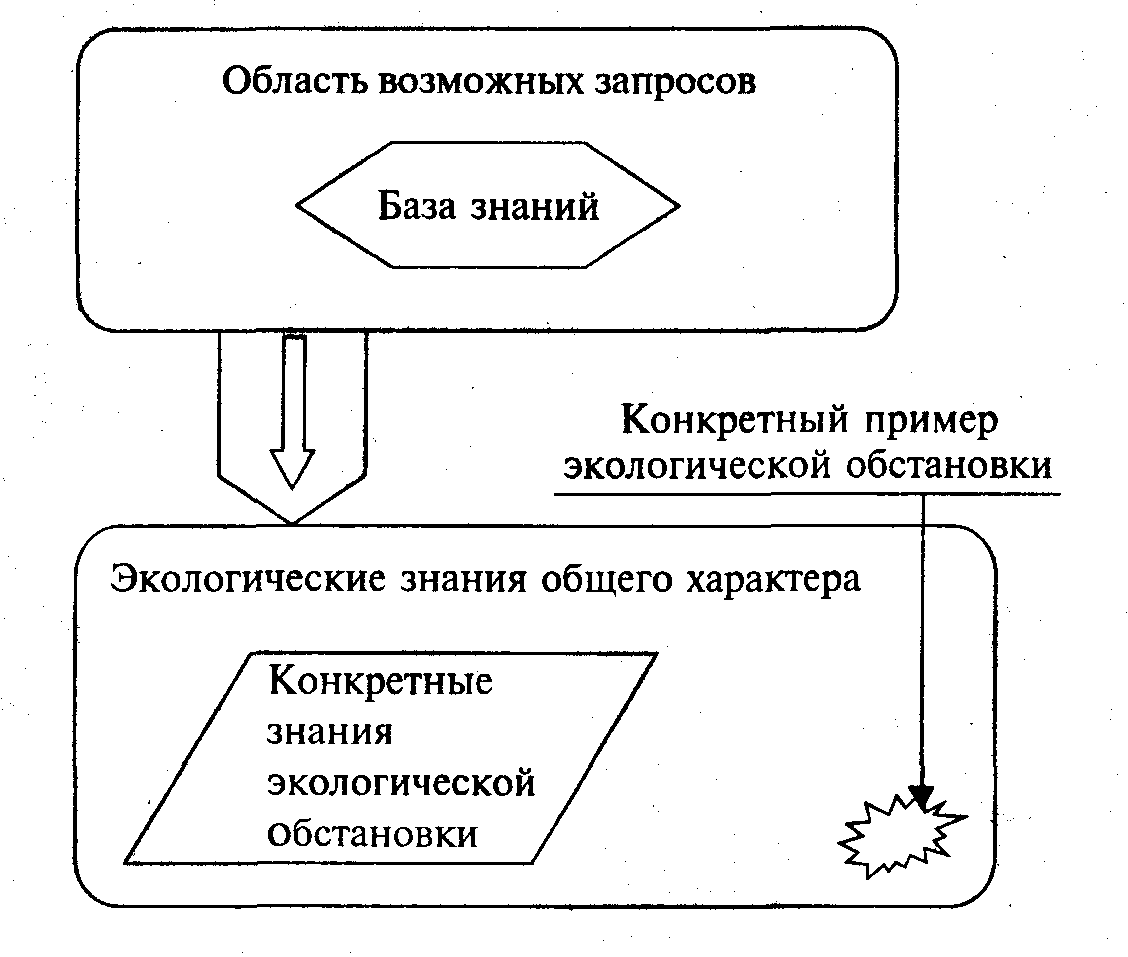
В общем виде ЭС содержат двумерный массив: область запросов и базу знаний (рис. 17.5).
Рис. 17.5. Схема базы данных и область запросов.
Область запросов — основной элемент ЭС. Если в область запросов попали какие-то данные, то систему можно запросить об этом.
База знаний содержит все знания ЭС по данному вопросу. Если запрос соответствует конкретным знаниям экологической обстановки ЭС, то ответ может быть получен немедленно.
Если вопрос касается конкретного примера экологической обстановки (рис. 6.5) с элементами экологических знаний обще- го характера, то ЭС вступает в диалог с пользователем до тех пор, пока не уточнит детали обстановки. После этого ЭС может выдать то или иное решение по данному вопросу.
ЭС могут быть более сложными, чем те, которые были рассмотрены. Например, машинно-обучающие экспертные системы.
назад
Специальные приложения.
Приложение 1
Значение функции
![]()
|
u |
F(u) |
u |
F(u) |
u |
F(u) |
u |
F(u) |
|
1 |
2 |
3 |
4 |
||||
|
-0,00 |
0,5000 |
-0,90 |
0,1841 |
0.00 |
0,5000 |
1,80 |
0,9641 |
|
-0,02 |
0,4920 |
-1,00 |
0,1587 |
0,02 |
0,5080 |
2,00 |
0,9772 |
|
-0,04 |
0,4840 |
-1,20 |
0,1151 |
0,04 |
05160 |
2,20 |
0,9861 |
|
-0,06 |
0,4761 |
-1,40 |
0,0808 |
0,06 |
0,5239 |
2,30 |
0,9893 |
|
-0,08 |
0,4681 |
-1,60 |
0,0548 |
0,08 |
0,5319 |
2,40 |
0,9918 |
|
-0,10 |
0,4602 |
-1,80 |
0,0359 |
0,10 |
0,5398 |
2,50 |
0,9938 |
|
-0,14 |
0,4443 |
-2,00 |
0,0228 |
0,14 |
0,5557 |
2,60 |
0,9953 |
|
-0,18 |
0,4286 |
-2,20 |
0,0139 |
0,18 |
0,5714 |
2,70 |
0,9965 |
|
-0,20 |
0,4207 |
-2,40 |
0,0082 |
0,20 |
0,5793 |
2,80 |
0,9974 |
|
-0,25 |
0,4013 |
-2,60 |
0,0047 |
0,25 |
0,5987 |
2,90 |
0,9981 |
|
-0,30 |
0,3821 |
-2,80 |
0,0026 |
0,30 |
0,6179 |
3,00 |
0,9986 |
|
-0,35 |
0,3632 |
-3,00 |
0,0014 |
0,35 |
0,6368 |
3,10 |
0,9990 |
|
-0,40 |
0,3446 |
-3,20 |
0,0007 |
0,40 |
0,6554 |
3,20 |
0,9993 |
|
-0,45 |
0,3264 |
-3,40 |
0,0003 |
0,45 |
0,6736 |
3,30 |
0,9995 |
|
-0,50 |
0,3085 |
-3,40 |
0,0002 |
0,50 |
0,6915 |
3,40 |
0,9997 |
|
-0,55 |
0,2912 |
-3,60 |
0,0001 |
0,60 |
0,7257 |
3,50 |
0,9998 |
|
-0,60 |
0,2743 |
-3,80 |
0,0000 |
0,70 |
0,7580 |
3,60 |
0,9998 |
|
-0,70 |
0,2420 |
-3,90 |
0 |
0,80 |
0,7881 |
3,70 |
0,9999 |
|
-0,80 |
0,2119 |
-3,9 |
|
1,00 |
0,8413 |
3,80 |
0,9999 |
|
|
|
|
|
1,20 |
0,8849 |
3,90 |
1,0000 |
|
|
|
|
|
1,40 |
0,9192 |
>3,9 |
1 |
|
|
|
|
|
1,60 |
0,9452 |
|
|
Приложение 2
Значение двухстороннего критерия
Стьюдента — tα. k при разных уровнях значимости
|
Число степеней свободы к
|
Уровни значимости |
|||
|
0,10 |
0,05 |
0,01 |
0,001 |
|
|
1 |
6,318 |
12,706 |
63,657 |
637,0 |
|
2 |
2,920 |
4,302 |
9,924 |
31,6 |
|
3 |
2,353 |
3,182 |
5,840 |
12,9 |
|
4 |
2,132 |
2,776 |
4,604 |
8,610 |
|
5 |
2,015 |
2,571 |
4,032 |
6,859 |
|
6 |
1,943 |
2,447 |
3,707 |
5,959 |
|
7 |
1,895 |
2,365 |
3,499 |
5,405 |
|
8 |
1,860 |
2,306 |
3,355 |
5,041 |
|
9 |
1,833 |
2,262 |
3,250 |
4,781 |
|
10 |
1,812 |
2,228 |
3,169 |
4,587 |
|
11 |
1,796 |
2,201 |
3,106 |
4,487 |
|
12 |
1,782 |
2,179 |
3,005 |
4,318 |
|
14 |
1,761 |
2,145 |
2,977 |
4,140 |
|
16 |
1,746 |
2,120 |
2,921 |
4,015 |
|
18 |
1,734 |
2,103 |
2,878 |
3,922 |
|
20 |
1,725 |
2,086 |
2,845 |
3,850 |
|
25 |
1,708 |
2,060 |
2,787 |
3,725 |
|
30 |
1,697 |
2,042 |
2,750 |
3,646 |
|
35 |
1,689 |
2,030 |
2,724 |
3,591 |
|
40 |
1,684 |
2,021 |
2,704 |
3,551 |
|
45 |
1,679 |
2,014 |
2,689 |
3,522 |
|
60 |
1,671 |
2,000 |
2,666 |
3,460 |
|
80 |
1,664 |
1990 |
2,639 |
3,416 |
|
100 |
1,660 |
1984 |
2,626 |
3,391 |
|
120 |
1,660 |
1980 |
2,620 |
3,370 |
|
∞ |
1,645 |
1960 |
2,576 |
3,291 |