ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 31.03.2024
Просмотров: 1070
Скачиваний: 0
СОДЕРЖАНИЕ
Математическое моделирование элементов сложных экологических систем
Лекция 1. Введение в моделирование. Исторический экскурс.
1. Основы моделирования в экологии 1.1. Общие принципы построения моделей в экологии
2.2. Этапы построения математической модели
1.4. Элементы теории подобия, применяемые в моделировании
3.2.2. Выборочный метод в экологометрике.
Зависимость числа интервалов от объема выборки
Статистический ряд по интервалам
Лекция 4. Статистические оценки параметров распределения случайных величин по выборкам
4.4. Статистические оценки гипотез об экологических моделях
Выборка из генеральной совокупности
Статистическая таблица эксперимента
Пример преобразования членов уравнения регрессии
Вычисление данных для линеаризации уравнения регрессии
Нормальные уравнения мнк для некоторых функций
Статистическое оценивание уравнения регрессии и парной корреляции.
Обработка результатов наблюдений
Рекомендации по выбору вида функции
3.4. Динамические статистические модели
Данные по объему сброса качественных сточных вод
Данные по объему сброса сточных вод за 5-летие
Пример расчета 5-летних средних
Расчетные значения для определения уравнения динамики
Ряд динамики для определения сезонных колебаний
Эксперименталъный материал исследования
8.1. Анализ влияния отдельных факторов в экологической модели.
Лекция 9. Методы оптимизации. Метод Лагранжа
Лекция 10. Метод линейного программирования.
Лекция 11. Функциональные модели.
Лекция 12. Модели процессов содержащие обыкновенные дифференциальные уравнения.
Численные ошибки использованных для вычисления данных
Лекция 13. Статистические модели динамики.
Лекция 16. Информационные технологии в экологии. Экологические информационные системы.
1 6.1. Экологические информационные системы
1. Какова область значения для числовых характеристик?
Лекция 17. Использование информационных технологий для решения задач экологии.
Критические значения коэффициента корреляции rk;α
2.1. Подобие физических явлений и его признаки
2.4. Применение методов подобия в математическом
11.3. Численные методы решения дифференциальных уравнений
11.3.2. Процесс численного решения
11.3.4. Модифицированный метод Эйлера
11.3.6. Метод Рунге – Кутта для систем дифференциальных уравнений
11.3.7. Общая характеристика одношаговых методов
11.3.9. Методы прогноза и коррекции
11.3.10. Краткая характеристика методов прогноза и коррекции.
11.3.11. Выбор шага и погрешность решения.
11.4. Имитационное моделирование систем
11.4.1. Принципы имитационного моделирования
11.4.3. Динамическая модель исследуемого объекта
11.4.4. Построение имитационных моделей динамических систем
11.4.5. Преобразование передаточных функций звеньев в дифференциальные уравнения в форме Коши
11.4.6. Синтез имитационной модели на основе структурной схемы
11.5. Теоретические основы построения математических моделей систем
11.5.1. Компонентные и топологические уравнения
11.5.2. Компонентные и топологические уравнения механической системы
11.5.3. Компонентные и топологические уравнения электрической системы
11.5.4. Компонентные и топологические уравнения гидравлической системы
11.5.5. Компонентные и топологические уравнения тепловой системы
11.6.1. Сущность метода электроаналогий.
11.6.2. Электромеханические аналогии
11.6.3. Построение имитационных моделей методом электроаналогий
11.6.4. Плоское прямолинейное движение звеньев
11.6.5. Электрогидравлические аналогии
11.4.6. Синтез имитационной модели на основе структурной схемы
Методику построения имитационной математической модели динамической системы рассмотрим на конкретном примере. Дана функциональная схема электромеханической следящей системы (рис.4.30). С помощью имитационного моделирования определить коэффициент усиления первого усилителя k1 из условия обеспечения устойчивости системы. Исходя из условия задачи, построим структурную схему электрической следящей системы (рис.4.31).
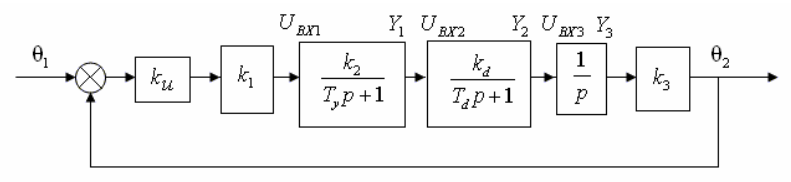
Рис. 4.31. Структурная схема
Данной структурной схеме соответствует определённая система дифференциальных уравнений в форме Коши. Чтобы определить эти уравнения, необходимо выполнить следующее:
1) Выделить на структурной схеме системы элементы (звенья), передаточные функции которых содержат в знаменателях операторы p , и обозначить входные и выходные величины таких элементов соответственно через UВХ и Y. Входным величинам элементов присваивают индекс, на единицу больший индекса выходной величины предыдущего элемента. Младший индекс входной величины принимают равным единице.
2) Записать дифференциальные уравнения звеньев, выражающие связь между входными и выходными величинами:
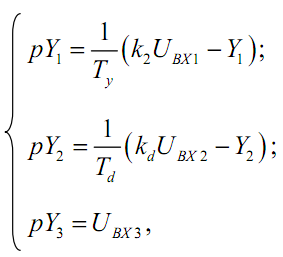
где
Y1
= U3
- напряжение
на выходе второго усилителя;
Y2
=
![]() -
скорость
вращения вала двигателя;
Y3
= θd
- угловое
перемещение вала двигателя.
-
скорость
вращения вала двигателя;
Y3
= θd
- угловое
перемещение вала двигателя.
3) Записать уравнения связей, показывающие условия соединения элементов между собой в составе структурной схемы:
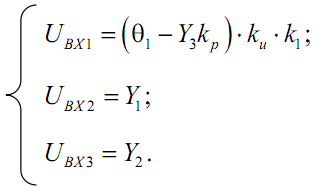
4) Подставив уравнения связей в дифференциальные уравнения звеньев, получить систему дифференциальных уравнений всей системы в форме Коши:
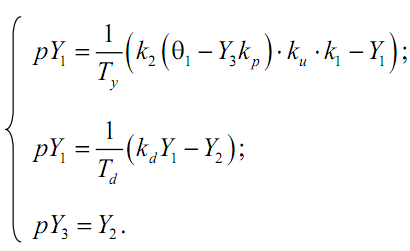
Для нахождения переходного процесса в исследуемой динамической системе, полученные уравнения следует проинтегрировать на ЭВМ при заданных начальных условиях.
В программе численного решения правые части дифференциальных уравнений можно вычислять в два этапа.
Сначала с помощью уравнений связей вычислить входные величины, UВХ1,..., UВХ2, а затем числовые значения этих величин подставить в дифференциальные уравнения звеньев.
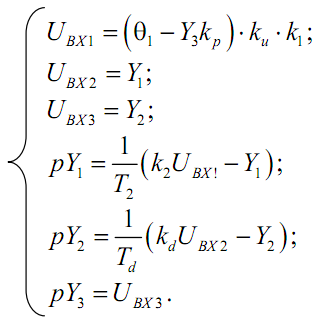
назад
11.5. Теоретические основы построения математических моделей систем
11.5.1. Компонентные и топологические уравнения
Основные физические свойства технических объектов любой физической природы – инерционные, упругие и диссипативные. Они отображаются в динамических моделях соответственно инерционными, упругими и диссипативными элементами.
При моделировании методом функционально законченных элементов элементы обычно обладают несколькими физическими свойствами и являются сложными. При имитационном моделировании все элементы простые, так как каждый из них наделён только одним физическим свойством. Мы в данном описании рассматриваем только простые элементы. Состояние простого элемента характеризуется одной потоковой переменной и одной потенциальной переменной. Зависимость между этими переменными называют компонентным уравнением.
Компонентные уравнения элементов могут быть получены путем непосредственного использования физических законов и имеют следующий вид:
1) для инерционного элемента
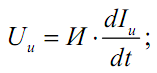 (5.1)
(5.1)
2) для диссипативного элемента
![]() (5.2)
(5.2)
3) для упругого элемента
![]() (5.3)
(5.3)
В уравнениях (5.1)-(5.3) приняты следующие обозначения: И, Д, У – параметры инерционного, диссипативного и упругого элементов соответственно; I – потоковая переменная; U – потенциальная переменная. Индексы при переменных I и U указывают на принадлежность их соответствующим элементам.
Для получения полной математической модели технической системы необходимо объединить все компонентные уравнения элементов в общую систему уравнений. Объединение осуществляется на основе физических законов, выражающих условия равновесия и непрерывности физических переменных. Уравнения этих законов называют топологическими уравнениями. Они описывают характер взаимодействия между простыми элементами, устанавливая соотношения между однотипными переменными. Условия равновесия записываются для потенциальных переменных:
![]()
а условия непрерывности – для потоковых переменных:
![]()
Форма компонентных и топологических уравнений одинакова для систем различной физической природы. Топологическое уравнение для векторных переменных формулируется как равенство нулю геометрической суммы
соответствующих координат, а для скалярных – равенство нулю алгебраической суммы этих координат.
Полная математическая модель технического объекта, составленная на основе компонентных уравнений, представляет собой систему обыкновенных дифференциальных уравнений.
Искомыми функциями в этих уравнениях являются базисные переменные (координаты) I и U, а независимой переменной – время t. Размерность математической модели определяется общим порядком системы дифференциальных уравнений (или числом базисных переменных). Эту модель обычно представляют в нормальной форме Коши, в которой все уравнения разрешены относительно первых производных координат dI/dt и dU/dt. Координатный базис в этом случае составляют потоковые переменные I и потенциальные переменные U.
11.5.2. Компонентные и топологические уравнения механической системы
а) Базисные переменные.
Сосредоточенные массы, отображаемые на динамических моделях механических систем, в силу позиционных связей могут совершать только простейшие виды движений – поступательное и вращательное, либо сложное движение, которое представляется сочетанием этих простейших видов. Поступательное движение твердого тела характеризуется линейной скоростью u и силой F, а вращательное – угловой скоростью ω и вращающим моментом M.
Они и принимаются в качестве базисных переменных механической системы:
потоковые переменные – скорость v(м/с) и ω(рад/с);
потенциальные переменные – силы F (Н) и моменты M (Н×м).
б) Параметры элементов.
Параметром инерционного элемента при поступательном движении является масса m(кг), а при вращательном движении момент инерции J(кг×м2).
Параметр диссипативного элемента – коэффициент сопротивления µ, называемый также коэффициентом вязкого трения или коэффициентом демпфирования. При поступательном движении измеряется в Н×с/м, а при вращательном – в Н×м×с/рад.
Параметр упругого элемента – коэффициент жёсткости С. При поступательном движении в качестве единицы измерения коэффициента С используется размерность Н/м, а при вращательном – Н×м/рад.
в) Компонентное уравнение инерционного элемента получают на основе второго закона Ньютона. Для поступательного движения твердого тела уравнение имеет вид:
![]()
а для вращательного –
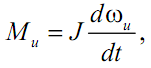
где и Fu , и Mu - соответственно сила инерции и момент сил инерции (или инерционный момент) элемента; vu, и ωu - скорости инерционного элемента.
Скорости vu и ωu представляют собой абсолютные скорости сосредоточенных масс соответственно при поступательном и вращательном движениях. Если твердое тело совершает сложное движение, то для каждого вида движения составляется свое компонентное уравнение инерционного элемента.
Математическое описание диссипативного элемента основано на использовании закона Стокса для вязкого трения. При поступательном движении компонентное уравнение имеет вид:
![]()
а при вращательном:
![]()
где Fд, Mд соответственно сила и момент вязкого трения; vд, ωд - скорости диссипативных элементов.
Согласно закону Гука, сила упругости деформируемого механического элемента пропорциональна величине деформации:
Fу = cΔ,
где Δ = x1- x2 - деформация элемента; x1, x2 – перемещения выделенных сосредоточенных масс; c - жесткость элемента.
Выражая перемещение x через базовые переменные v или ω, получаем следующие компонентные уравнения упругих элементов.
При поступательном движении:
![]()
При вращательном движении:
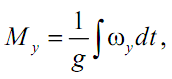
где Fу, Mу - соответственно сила и момент упругих элементов; g = 1/c - податливость элемента. Упругие и диссипативные элементы в динамической модели соединяют между собой сосредоточенные массы. В этой связи, скорости указанных элементов vу, ωу, vд, ωд представляют собой относительные скорости соединяемых ими сосредоточенных масс:
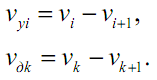
Силы Fи, Fд, Fу и моменты Mи, Mд, Mу инерционных, диссипативных и упругих элементов характеризуют их взаимодействия в динамической модели. Они представляют собой внутренние силы системы. При движении системы под действием приложенных к ней внешних сил и моментов происходит изменение её кинетической и потенциальной энергии, а часть энергии затрачивается на преодоление сил трения. Инерционные элементы динамической системы отображают свойство системы накапливать кинетическую энергию, упругие элементы – свойство накапливать потенциальную энергию, а диссипативные – рассеивать энергию путем превращения механической энергии в тепловую энергию.
г) Топологические уравнения.
Первое топологическое уравнение является уравнением равновесия, его выражает принцип Даламбера: геометрическая сумма всех сил приложенных к твердому телу, включая силу инерции, равна нулю: