ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 31.03.2024
Просмотров: 1111
Скачиваний: 0
СОДЕРЖАНИЕ
Математическое моделирование элементов сложных экологических систем
Лекция 1. Введение в моделирование. Исторический экскурс.
1. Основы моделирования в экологии 1.1. Общие принципы построения моделей в экологии
2.2. Этапы построения математической модели
1.4. Элементы теории подобия, применяемые в моделировании
3.2.2. Выборочный метод в экологометрике.
Зависимость числа интервалов от объема выборки
Статистический ряд по интервалам
Лекция 4. Статистические оценки параметров распределения случайных величин по выборкам
4.4. Статистические оценки гипотез об экологических моделях
Выборка из генеральной совокупности
Статистическая таблица эксперимента
Пример преобразования членов уравнения регрессии
Вычисление данных для линеаризации уравнения регрессии
Нормальные уравнения мнк для некоторых функций
Статистическое оценивание уравнения регрессии и парной корреляции.
Обработка результатов наблюдений
Рекомендации по выбору вида функции
3.4. Динамические статистические модели
Данные по объему сброса качественных сточных вод
Данные по объему сброса сточных вод за 5-летие
Пример расчета 5-летних средних
Расчетные значения для определения уравнения динамики
Ряд динамики для определения сезонных колебаний
Эксперименталъный материал исследования
8.1. Анализ влияния отдельных факторов в экологической модели.
Лекция 9. Методы оптимизации. Метод Лагранжа
Лекция 10. Метод линейного программирования.
Лекция 11. Функциональные модели.
Лекция 12. Модели процессов содержащие обыкновенные дифференциальные уравнения.
Численные ошибки использованных для вычисления данных
Лекция 13. Статистические модели динамики.
Лекция 16. Информационные технологии в экологии. Экологические информационные системы.
1 6.1. Экологические информационные системы
1. Какова область значения для числовых характеристик?
Лекция 17. Использование информационных технологий для решения задач экологии.
Критические значения коэффициента корреляции rk;α
2.1. Подобие физических явлений и его признаки
2.4. Применение методов подобия в математическом
11.3. Численные методы решения дифференциальных уравнений
11.3.2. Процесс численного решения
11.3.4. Модифицированный метод Эйлера
11.3.6. Метод Рунге – Кутта для систем дифференциальных уравнений
11.3.7. Общая характеристика одношаговых методов
11.3.9. Методы прогноза и коррекции
11.3.10. Краткая характеристика методов прогноза и коррекции.
11.3.11. Выбор шага и погрешность решения.
11.4. Имитационное моделирование систем
11.4.1. Принципы имитационного моделирования
11.4.3. Динамическая модель исследуемого объекта
11.4.4. Построение имитационных моделей динамических систем
11.4.5. Преобразование передаточных функций звеньев в дифференциальные уравнения в форме Коши
11.4.6. Синтез имитационной модели на основе структурной схемы
11.5. Теоретические основы построения математических моделей систем
11.5.1. Компонентные и топологические уравнения
11.5.2. Компонентные и топологические уравнения механической системы
11.5.3. Компонентные и топологические уравнения электрической системы
11.5.4. Компонентные и топологические уравнения гидравлической системы
11.5.5. Компонентные и топологические уравнения тепловой системы
11.6.1. Сущность метода электроаналогий.
11.6.2. Электромеханические аналогии
11.6.3. Построение имитационных моделей методом электроаналогий
11.6.4. Плоское прямолинейное движение звеньев
11.6.5. Электрогидравлические аналогии
11.6.6. Электротепловые аналогии
Требуется построить имитационную модель теплового процесса, который происходит при нагреве штампа для горячего прессования пластмасс.
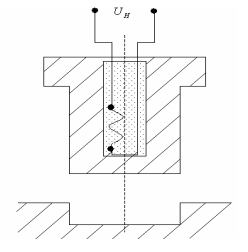
Рис. 6.41. Конструктивная схема штампа
Конструкция штампа содержит встроенный электронагревательный элемент (рис. 6.41). Рассмотрим процесс передачи тепла через тело штампа (рис.6.42).
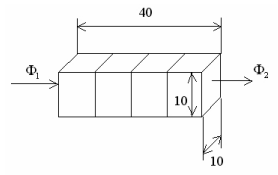
Рис. 6.42. Процесс передачи тепла
Тепловой поток от нагревателя Ф1 проходит последовательно через цепь выделенных элементов. Поперечное сечение элементов заданно. Количество элементов в данном случае - 4. Проходя через теплопроводящую цепь элементов, тепловой поток преодолевает тепловое сопротивление этих элементов. Кроме того, часть теплового потока идет на потери тепла, связанные с теплоемкостью металла, из которого изготовлен штамп. Поэтому тепловой поток, проходящий через наружную поверхность Ф2< Ф1. Эквивалентная электрическая схема замещения представляет собой линию задержки, состоящую из последовательно включенных RC-цепочек (рис. 6.43). Активное сопротивление цепочки имитирует тепловое сопротивление, а электрическая емкость – теплоемкость элемента.
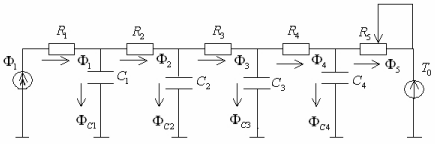
Рис. 6.43. Эквивалентная электрическая схема
Последнее сопротивление тепловой цепи R5 переменное. Это обусловлено тем, что во время прессования тепловое сопротивление среды, соприкасающейся с поверхностью штампа, уменьшается. В результате поверхность штампа охлаждается. По окончании прессования штамп поднимается вверх и оказывается в воздушной среде. При этом благодаря низкой теплопроводности воздуха поверхность штампа разогревается.
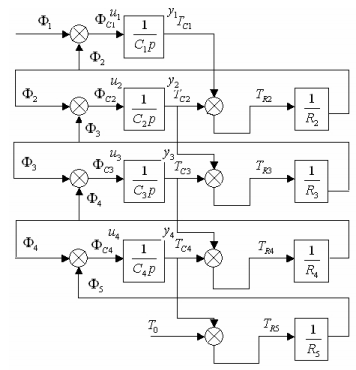
Рис. 6.44. Структурная схема
Таким образом, температура поверхности штампа не остается постоянной. Она периодически изменяется от минимального значения до максимального значения. Чтобы построить структурную схему математической модели, надо определить тепловой поток Ф1, проходящий через поперечное сечение элементов. Весь тепловой поток, излучаемый электрическим нагревателем, равен мощности этого нагревателя, а часть теплового потока, приходящаяся на поперечное сечение элемента, во столько раз меньше, во сколько раз поперечное сечение элемента меньше площади всей поверхности штампа.
Электрической схеме замещения соответствует структурная схема математической модели (рис. 6.44).
Непосредственно из структурной схемы следуют уравнения связи.
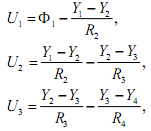
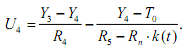
где
![]()
где, в свою очередь,
![]()
а T - полупериод рабочего цикла. Переходные процессы в интегрирующих звеньях определяются с помощью следующих дифференциальных уравнений.
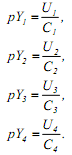
Коэффициенты модели определим исходя из того, что материал штампа - железо. Для железа:
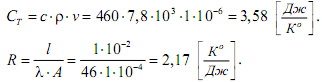
Примем
![]() ,
,![]() ,
,![]()
Графики переходных процессов (рис. 6.45) показывают, что при заданном режиме работы температура поверхности штампа изменяется в пределах от 198оС до 144оС. Время нагрева штампа до заданной температуры составляет ок. 200 c .
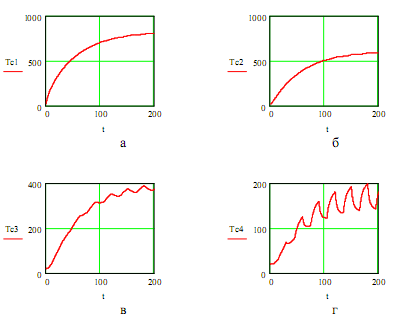
Рис. 6.45
Рассмотренная методика синтеза имитационных моделей имеет как преимущества, так и недостатки. Преимущество этой методики в том, что синтез имитационной модели сопровождается построением структурной схемы динамической системы. Поскольку структурная схема содержит передаточные функции всех звеньев, то появляется возможность исследовать динамическую систему с привлечением методов теории управления. Однако такое моделирование оправдано лишь для сравнительно простых систем, содержащих небольшое количество звеньев. С повышением сложности системы количество передаточных функций и уравнений связи, которые рассчитываются вручную, возрастает, и работа становится громоздкой и трудоемкой. Чтобы облегчить синтез сложных моделей, применяют компьютерное моделирование, основанное на структурно - матричных представлениях метода электроаналогии, либо специальные программные средства моделирования, такие как Matlab, Mathcad, Anylogic и др.
назад
Приложение III
ВСТРОЕННЫЕ ФУНКЦИИ MATHCAD
|
Функция |
Описание |
|||||||||||
|
acos(z) |
Возвращает величину (в радианах) угла, косинус которого равен z При комплексном z возвращает главное значение величины угла |
|||||||||||
|
acosh(z) |
Возвращает величину (в радианах) угла, гиперболический косинус которого равен z. При комплексном z возвращает главное значение величины угла |
|||||||||||
|
acot(z) |
Возвращает величину (в радианах) угла, котангенс которого равен z и который находится в (0, π). При комплексном z возвращает главное значение величины угла |
|||||||||||
|
Функция |
Описание |
|||||||||||
|
acoth(z) |
Возвращает величину (в радианах) угла, гиперболический котангенс которого равен z. При комплексном z возвращает главное значение величины угла |
|||||||||||
|
acsc(z) |
Возвращает величину (в радианах) угла, косеканс которого равен z. При комплексном z возвращает главное значение величины угла |
|||||||||||
|
acsch(z) |
Возвращает величину (в радианах) угла, гиперболический косеканс которого равен z. При комплексном z возвращает главное значение величины угла |
|||||||||||
|
Adams(у, x1, χ2 , npoints, D [, tol]) |
Возвращает матрицу приближенных значений решения на интервале [x1, х2] задачи Коши для нормального дифференциального уравнения, правые части которого определены в d, а начальное значение в точке x1 равно у. Приближенное решение вычислено методом Адамса. Параметр npoints задает число строк матрицы результатов (или количество узлов сетки на интервале [x1, х2]) |
|||||||||||
|
AdamsBDF(у,x1,x2,npoints,D[, J] [, tol]) |
Возвращает матрицу приближенных значений решения на интервале [x1, х2] задачи Коши для нормального дифференциального уравнения, правые части которого определены в d, а начальное значение в точке xl равно у. Для жестких систем приближенное решение вычисляется BDF-методом, для нежестких — методом Адамса. Параметр npoints задает число строк матрицы результатов (количество узлов сетки на интервале [xl, х2]) |
|||||||||||
|
Ai (z) |
Возвращает значение функции Эйри первого рода |
|||||||||||
|
Ai.sc(x) |
Возвращает значение функции Эйри первого рода с коэффициентом масштабирования Re(ехр(2/3*z^(3/2))) |
|||||||||||
|
angle(x, y) |
Возвращает величину (в радианах) угла (от 0 до 2π), образованного положительным направлением оси абсцисс и радиусом-вектором точки плоскости с координатами (х, у), x и у должны быть вещественными |
|||||||||||
|
antisymmetric tensor(i, j, k) (вид в Mathcad-документе: ε(i, j, k)) |
Возвращает полностью антисимметричный тензор третьего ранга. Результат равен 0, если любые два аргумента совпадают, 1 при четной перестановке и -1 при нечетной перестановке |
|||||||||||
|
APPENDPRN(file[, M]) |
Записывает содержимое массива в конец ASCII- файла с разделителями |
|||||||||||
|
Функция |
Описание |
|||||||||||
|
arg(z) |
Возвращает главное значение аргумента комплексного числа z Главное значение находится в интервале (-π, π] |
|||||||||||
|
asec (z) |
Возвращает величину угла (в радианах), секанс которого равен z. При комплексном z возвращает главное значение величины угла |
|||||||||||
|
asech(z) |
Возвращает величину угла (в радианах), гиперболический секанс которого равен z. При комплексном z возвращает главное значение величины угла |
|||||||||||
|
asin(z) |
Возвращает величину угла (в радианах), синус которого равен z. При комплексном z возвращает главное значение величины угла |
|||||||||||
|
asinh(z) |
Возвращает величину угла (в радианах), гиперболический синус которого равен z. При комплексном z возвращает главное значение величины угла |
|||||||||||
|
atan(z) |
Возвращает величину угла (в радианах), тангенс которого равен z. При комплексном z возвращает главное значение величины угла |
|||||||||||
|
atan2(x, у) |
Возвращает величину (в радианах) угла (от -π до π), образованного положительным направлением оси абсцисс и радиусом-вектором точки плоскости с координатами (х, у), x и у должны быть вещественными |
|||||||||||
|
atanh(z) |
Возвращает величину угла (в радианах), гиперболический тангенс которого равен z. При комплексном z возвращает главное значение величины угла |
|||||||||||
|
augment(А, В, С, ...) |
Возвращает массив, полученный в результате размещения массивов A, B, C, ... слева направо |
|||||||||||
|
BDF(у, x1, х2, npoints, D [, J] [, tol]) |
Возвращает матрицу приближенных значений решения задачи Коши для жесткого нормального ОДУ с правыми частями, определенными в D. Начальное значение в точке x1 равно у. Решение вычисляется в npoints точках из [x1, χ2] BDF-методом |
|||||||||||
|
bei(m, x) |
Возвращает значение мнимой части функции Кельвина порядка m |
|||||||||||
|
ber(m, x) |
Возвращает значение вещественной части функции Кельвина порядка m |
|||||||||||
|
Bi(x) |
Возвращает значение функции Эйри второго рода |
|||||||||||
|
Функция |
Описание |
|
||||||||||
|
Bi.sc(x) |
Возвращает значение функции Эйри второго рода с коэффициентом масштабирования ехр(-|Re(2/3*z^3/2)|) |
|
||||||||||
|
bspline(vx, vy, u, n) |
Возвращает вектор коэффициентов B - сплайна степени n для данных в νx и vy при заданных узловых значениях в u. Возвращаемый вектор становится первым аргументом функции interp |
|
||||||||||
|
Bulstoer(y, x1, x2, npoints, D) |
Возвращает матрицу приближенных значений решения задачи Коши для нормального ОДУ с гладкими, правыми частями, определенными в D. Начальное значение в точке x1 равно у. Решение вычисляется в npoints точках из [x1, х2] методом Булирша — Штера |
|
||||||||||
|
bvalfit(vl, v2, x1, x2, xf, D, load1, load2, score) |
Возвращает вектор недостающих граничных условий в краевой задаче для ОДУ с правыми частями, определенными в D, с условием score в промежуточной точке x1 и граничными условиями load1, load2 на концах [x1, х2] |
|
||||||||||
|
Ceil(z, у) |
Возвращает значение произведения (l+[z/y])*у |
|
||||||||||
|
ceil(z) |
Возвращает значение 1+ [z], (целую часть z, увеличенную на 1) |
|
||||||||||
|
CFFT(A) |
Возвращает массив коэффициентов дискретного преобразования Фурье (одномерного или двумерного) сигнала а, заданного значениями, с нормирующим множителем 1/n^1/2 |
|
||||||||||
|
cfft(A) |
Возвращает массив коэффициентов дискретного преобразования Фурье (одномерного или двумерного) сигнала а, заданного n значениями, с нормирующим множителем 1/n |
|
||||||||||
|
Chi(χ) |
Возвращает значение интегрального гиперболического косинуса х. Может быть вычислена только аналитически |
|
||||||||||
|
cholesky(Μ) |
Возвращает квадратный корень из положительно определенной матрицы M (т.е. матрицу L из разложения Холецкого) |
|
||||||||||
|
Ci (x) |
Возвращает значение интегрального косинуса х. Может быть вычислена только аналитически |
|
||||||||||
|
cnorm(χ) |
Возвращает значение в точке χ функции распределения стандартного нормального распределения |
|
||||||||||
|
|
|
|
||||||||||
|
Функция |
Описание |
|
||||||||||
|
cnper(rate, pv, fv) |
Возвращает число периодов начисления сложных процентов, необходимое для получения дохода от инвестиций, равного указанной будущей стоимости |
|
||||||||||
|
cols(A)
|
Возвращает число столбцов в A |
|
||||||||||
|
combinfn, k) |
Возвращает число сочетаний из n по к |
|
||||||||||
|
concat(SI, S2, S3, . . . )
|
Возвращает строку, образованную объединением строк si, S2 и т. д. |
|
||||||||||
|
condl(Μ) |
Возвращает число обусловленности матрицы м, вычисленное в норме L1 Л |
|
||||||||||
|
cond2(Μ) |
Возвращает число обусловленности матрицы м, вычисленное в норме L2 |
|
||||||||||
|
conde(Μ) |
Возвращает число обусловленности матрицы м, вычисленное в евклидовой норме |
|
||||||||||
|
condi(Μ) |
Возвращает число обусловленности матрицы м, вычисленное в бесконечной норме |
|
||||||||||
|
corr(A, В) |
Возвращает коэффициент корреляции Пирсона элементов из A и B |
|
||||||||||
|
correl(vx, vy) |
Вычисляет корреляцию векторов vx и vy. Результатом является вектор, в котором каждый элемент содержит суммарное векторное произведение vx и смещенного варианта vy |
|
||||||||||
|
correl2d(Μ, K) |
Возвращает 2D-корреляцию матрицы M с ядром K. Результирующая матрица содержит суммарное поэлементное произведение K, перекрывающееся с подмножеством M |
|
||||||||||
|
cos(z)
|
Возвращает значение косинуса z |
|
||||||||||
|
cosh(z) |
Возвращает значение гиперболического косинуса z |
|
||||||||||
|
cot(z) |
Возвращает значение котангенса z |
|
||||||||||
|
coth(z) |
Возвращает значение гиперболического котангенса z |
|
||||||||||
|
Функция |
Описание |
|
||||||||||
|
crate(nper, pv, fv) |
Возвращает фиксированную процентную ставку на период, необходимую, чтобы инвестиции с текущей стоимостью позволили получить указанную будущую стоимость через определенное число периодов начисления сложных процентов |
|
||||||||||
|
CreateMesh(function(s) [, s0, s1, t0, t1] [, sgrid, tgrid] [, fmap]) |
Возвращает вложенный массив из трех матриц, представляющих координаты х, у и z параметрической поверхности, определенной функцией (функциями) с двумя переменными в первом аргументе (аргументах) |
|
||||||||||
|
CreateSpace(function(s) [, t0, t1] [, tgrid] [ , fmap]) |
Возвращает вложенный массив из трех векторов, представляющих координаты х, у и z пространственной кривой, определенной функцией (функциями) с одной переменной в первом аргументе |
|
||||||||||
|
csc(z) |
Возвращает значение косеканса z |
|
||||||||||
|
csch(z) |
Возвращает значение гиперболического косеканса z |
|
||||||||||
|
csgn(z) |
Возвращает комплексный знак ζ, заданный значением 0, если ζ = 0, значением 1, если вещественная или Мнимая часть ζ > 0, и значением -1 в противном случае |
|
||||||||||
|
csort(A, n) |
Возвращает массив, образованный перестановкой строк матрицы А с упорядоченным по возрастанию n-м столбцом |
|
||||||||||
|
cspline(vx, vy)
|
Возвращает вектор коэффициентов интерполяционного кубического сплайна функции, заданной значениями vy в узлах νx. Этот вектор становится первым аргументом функции interp |
|
||||||||||
|
cumintfrate, nper, pv, start, end [, type]) |
Возвращает накопленный процент, выплачиваемый по ссуде в промежутке от начального до конечного периода при заданных фиксированной процентной ставке, числе периодов начисления сложных процентов и текущей стоимости ссуды |
|
||||||||||
|
cumprn(rate, nper, pv, start, end [, type]) |
Возвращает накопленную основную сумму, выплачиваемую по ссуде в промежутке от начального до конечного периода при заданной фиксированной процентной ставке, числе периодов начисления сложных процентов и текущей стоимости ссуды |
|
||||||||||
|
cvar(A, B) |
Возвращает ковариацию A и B |
|
||||||||||
|
cyl2xyz(r, q, f) |
Возвращает декартовы координаты точки с заданными цилиндрическими координатами |
|
||||||||||
|
Функция |
Описание |
|
||||||||||
|
DAi(z) |
Значение первой производной функции Эйри первого рода |
|
||||||||||
|
DAi.sc(z) |
Значение первой производной функции Эйри первого рода с коэффициентом масштабирования Re(ехр(2/3*z^(3/2))) |
|
||||||||||
|
dbeta(x,si,s2) |
Возвращает значение в точке χ плотности вероятности для бета-распределения |
|
||||||||||
|
DBi(z) |
Значение первой производной функции Эйри второго рода |
|
||||||||||
|
DBi.sc(z) |
Значение первой производной функции Эйри второго рода с коэффициентом масштабирования ехр(-|Re(2/3*z^3/2) |
|
||||||||||
|
dbinom(k,η,q) |
Возвращает плотность вероятности биномиального распределения |
|
||||||||||
|
dcauchy(x,1,s) |
Возвращает значение в точке x плотности вероятности распределения Коши |
|
||||||||||
|
dchisq(x,d) |
Возвращает значение в точке x плотности вероятности распределения x2 |
|
||||||||||
|
denorm(x) |
Возвращает знаменатель рационального выражения х. Может быть вычислена только аналитически |
|
||||||||||
|
dexp(x,r) |
Возвращает значение в точке x плотности вероятности экспоненциального распределения |
|
||||||||||
|
dF(x,dl, d2 ) |
Возвращает значение в точке х плотности вероятности распределения Фишер |
|
||||||||||
|
dgamma(χ, s) |
Возвращает значение в точке х плотности вероятности гамма-распределения |
|
||||||||||
|
dgeom(k,p) |
Возвращает значение в точке х плотности вероятности геометрического распределения |
|
||||||||||
|
dhypergeom(m, a, b, n) |
Возвращает значение в точке х плотности вероятности гипергеометрического распределения |
|
||||||||||
|
diag(v) |
Возвращает диагональную матрицу с диагональю ν |
|
||||||||||
|
dilog(x) |
Возвращает значение дилогарифма. Может быть вычислена только аналитически |
|
||||||||||
|
dlnorm(x, mu, sigma) |
Возвращает значение в точке х плотности вероятности логнормального распределения |
|
||||||||||
|
dlogis(x, 1, s) |
Возвращает значение в точке х плотности вероят- ности логистического распределения |
|
||||||||||
|
Функция |
Описание |
|
||||||||||
|
DMS (х) |
Возвращает угол в радианах, если x — вектор, содержащий градусы, минуты и секунды. В местоза- полнителе единиц измерения преобразует ответ в вектор, содержащий градусы, минуты и секунды |
|
||||||||||
|
dnbinom(k, η, ρ) |
Возвращает значение в точке x плотности вероятности отрицательного биномиального распределения |
|
||||||||||
|
dnorm(x, mu, sigma) (см. рис. 6.41) |
Возвращает значение в точке x плотности вероятности нормального распределения |
|
||||||||||
|
dpois(k, 1) |
Возвращает значение в точке x плотности вероятности распределения Пуассона |
|
||||||||||
|
dt(χ, d) |
Возвращает значение в точке x плотности вероятности распределения Стьюдента |
|
||||||||||
|
dunif(x, a, b) |
Возвращает значение в точке x плотности вероятности равномерного распределения на интервале [а,Ь] |
|
||||||||||
|
dweibull(x, s) |
Возвращает значение в точке x плотности вероятности распределения Вейбулла |
|
||||||||||
|
eff(rate, npery) |
Возвращает действующую годовую процентную ставку (APR) при заданных номинальной процентной ставке и числе периодов начисления сложных процентов за год |
|
||||||||||
|
Ei (x) |
Возвращает значение в точке x интегральной показательной функции |
|
||||||||||
|
eigenvals(M) |
Возвращает собственные значения квадратной матрицы M |
|
||||||||||
|
eigenvec(M, z) |
Возвращает собственный вектор квадратной матрицы M, отвечающий собственному значению z |
|
||||||||||
|
eigenvecs(M) |
Возвращает матрицу, столбцы которой — собственные векторы квадратной матрицы M, отвечающие собственным значениям, вычисленным функцией eigenvals(Μ) |
|
||||||||||
|
erf(z) |
Возвращает значение интеграла вероятностей в точке z |
|
||||||||||
|
erfc(x) |
Возвращает значение дополнительного интеграла вероятностей в точке z |
|
||||||||||
|
error(S) |
Возвращает строку s в качестве совета по устранению ошибки Mathcad |
|
||||||||||
|
Функция |
Описание |
|
||||||||||
|
ехр(z) |
Возвращает значение е в степени z |
|
||||||||||
|
expfit(vx, vy [,vg]) |
Возвращает значения коэффициентов а, b, с функции вида а*е(b*х) +с, аппроксимирующей функцию, заданную значениями vy в точках vx; vg содержит начальное приближение для этих трех коэффициентов |
|
||||||||||
|
FFT(v) |
Возвращает массив коэффициентов быстрого дискретного преобразования Фурье сигнала ν, заданного 2^n значениями, с нормирующим множителем 1/(2^n)^1/2 |
|
||||||||||
|
fft(ν) |
Возвращает массив коэффициентов быстрого дискретного преобразования Фурье сигнала ν, заданного 2^n значениями, с нормирующим множителем ½^n |
|
||||||||||
|
fhyper(a, b, с, χ) |
Возвращает значение суммы ряда Гаусса в точке x |
|
||||||||||
|
FIF(χ) |
Возвращает величину с единицами длины, если x — строка "футы-дюймы-доли дюймов". В место- заполнителе единиц измерения преобразует ответ в строку "футы-дюймы-доли дюймов" |
|
||||||||||
|
Find(var1, var2, ...) |
Возвращает значения переменных var1, var2,..., представляющие решение системы уравнений в блоке решения. Если указан только один аргумент, возвращает скаляр, иначе возвращает вектор. Требует первого приближения значений переменных var1, var2,... Щелкните правой кнопкой мыши по имени этой функции для выбора численного метода решения. Работает и с численной, и с символьной математикой |
|
||||||||||
|
Floor(z, у) |
Возвращает значение произведения [z/у] *у — произведения целой части z/у на у |
|
||||||||||
|
floor(z)
|
Возвращает целую часть z |
|
||||||||||
|
format(S, x, у, z, |
Возвращает строку, содержащую значения аргументов х, у, z,... с указанием очередности печати и сопровождающим текстом, заданным параметром s. Параметр s необязателен, если печатается только одно значение |
|
||||||||||
|
FresnelC(x) |
Возвращает значение интеграла Френеля с (х) |
|
||||||||||
|
Функция |
Описание |
|
||||||||||
|
FresnelS(x) |
Возвращает значение интеграла Френеля s (x) |
|
||||||||||
|
fv(rate, nper, pmt t, [pv] [, type]]) |
Возвращает будущую стоимость инвестиции или ссуды, если заданы периодический платеж постоянной величины и фиксированная процентная ставка |
|
||||||||||
|
fvadj(prin, v) |
Возвращает будущую стоимость начальной основной суммы после применения последовательности ставок сложных процентов в векторе ν |
|
||||||||||
|
fvc(rate, v) |
Возвращает будущую стоимость вектора денежных потоков ν, исходя из заданной процентной ставки |
|
||||||||||
|
Gamma([a], z) |
Возвращает значение гамма-функции в точке z либо значение неполной гамма-функции с параметром а |
|
||||||||||
|
gcd(А, В, С, . . . ) |
Возвращает наибольший общий делитель А, B, C, ... |
|
||||||||||
|
genfit(vx, vy, vg, F) |
Возвращает вектор значений, обеспечивающих наилучшее приближение первой функции f к значениям в векторах νx и vy. (Если F — вектор, то остальные элементы вектора F являются частными производными аппроксимирующей функции по ее n аргументам.) Вектор vg — начальные приближения. Щелкните функцию правой кнопкой мыши для выбора решателя |
|
||||||||||
|
geninv(A) |
Возвращает обобщенную обратную (псевдообратную) матрицу для матрицы А |
|
||||||||||
|
genvals(M, N) |
Возвращает собственные значения для обобщенной проблемы собственных значений пары матриц Μ, N |
|
||||||||||
|
genvecs(Μ, N) |
Возвращает матрицу, столбцами которой являются собственные векторы для обобщенной проблемы собственных значений пары матриц M, N, отвечающие обобщенным собственным векторам, вычисленным функцией genvals (Μ,. Ν) |
|
||||||||||
|
GETWAVINFO(file) |
Возвращает вектор, содержащий элементы в следующем порядке: число каналов, частота выборки, разрешение в битах и средний поток (число байтов в секунду) для WAV-файла |
|
||||||||||
|
gmean(А, В, C, ...) |
Возвращает среднее геометрическое элементов А,B,C,... |
|
||||||||||
|
H1(m, z) |
Значение функции Ганкеля первого рода (функции Бесселя третьего рода) |
|
||||||||||
|
|
|
|
||||||||||
|
Функция |
Описание |
|
||||||||||
|
H1. sc (m, z) |
Значение функции Ганкеля первого рода (функции Бесселя третьего рода) с коэффициентом масштабирования exp(-z*i) |
|
||||||||||
|
H2 (m, z) |
Значение функции Ганкеля второго рода (функции Бесселя третьего рода) |
|
||||||||||
|
H2. sc (m, z) |
Возвращает значение в точке z функции Бесселя третьего рода (функции Ханкеля второго рода) с коэффициентом масштабирования ехр (z * i) |
|
||||||||||
|
heaviside step(x) |
Возвращает значение функции Хевисайда в точке x. Имя функции (прописная греческая Φ (фи)) набирается через панель греческих букв |
|
||||||||||
|
Her(n, x) |
Возвращает значение в точке x полинома Эрмита степени n |
|
||||||||||
|
hhmmss(x) |
Возвращает время, если задана строка формата "часы:минуты:секунды". Возвращает такую строку, если задано время, при использовании в местозаполнителе единиц измерения |
|
||||||||||
|
hist(intvls, data) |
Возвращает частоты, с которыми значения из data данных попадают в интервалы, заданные параметром intvls. Параметр intvls может определять границы интервалов или их количество |
|
||||||||||
|
histogram(intvls, data)
|
Возвращает матрицу, первый столбец которой содержит координаты середин подынтервалов, заданных в переменной intvls, а второй столбец — соответствующие частоты для данных в векторе data |
|
||||||||||
|
hlookup(z, A, r) |
Возвращает значение элемента матрицы а, расположенного в z-м столбце, r-й строке |
|
||||||||||
|
hmean(А, В, С, .. . ) |
Возвращает среднее гармоническое элементов а, в, с, ... |
|
||||||||||
|
I0(z) |
Возвращает значение в точке z модифицированной функции Бесселя первого рода нулевого порядка |
|
||||||||||
|
I0.sc(z) |
Возвращает значение в точке z модифицированной функции Бесселя первого рода нулевого порядка с коэффициентом масштабирования ехр(-|Re(z)|) |
|
||||||||||
|
I1(z) |
Возвращает значение в точке z модифицированной функции Бесселя первого рода первого порядка |
|
||||||||||
|
I1.sc(z) |
Возвращает значение в точке z модифицированной функции Бесселя первого рода первого порядка с коэффициентом масштабирования ехр(-|Re(z)) |
|
||||||||||
|
Функция |
Описание |
|
||||||||||
|
ibeta(a, χ, у) |
Возвращает значение неполной бета-функции от x и у с параметром а |
|
||||||||||
|
ICFFT(A) |
Обратное преобразование Фурье для CFFT |
|
||||||||||
|
icfft(A) |
Обратное преобразование Фурье для cfft |
|
||||||||||
|
identity(η) |
Возвращает единичную матрицу размерности n |
|
||||||||||
|
if(cond, x, у) |
Возвращает х, если логическое условие cond истинно, иначе возвращает у |
|
||||||||||
|
IFFT(u) |
Обратное преобразование Фурье для FFT |
|
||||||||||
|
ifft(u) |
Обратное преобразование Фурье для fft |
|
||||||||||
|
Im (z) |
Возвращает мнимую часть z |
|
||||||||||
|
In(m, z) |
Возвращает значение в точке z модифицированной функции Бесселя первого рода m-гo порядка |
|
||||||||||
|
In.sc(m, z) |
Возвращает значение в точке z модифицированной функции Бесселя первого рода m-го порядка с коэффициентом масштабирования ехр(-|Re(z)|) |
|
||||||||||
|
intercept(vx, vy) |
Возвращает значение константы b из уравнения линии регрессии у = ах+b для данных vx, vy |
|
||||||||||
|
Interp(vs, vx, vy, x) |
Возвращает значение в точке x сплайна, коэффициенты которого в vs вычислены по данным vx, vy одной из функций cspline, lspline, pspline, bspline,loess и regress |
|
||||||||||
|
ipmt(rate,per,nper,pv[, [fv] [, type]]) |
Возвращает размер выплаты процентов по вкладу или ссуде для заданного периода при условии периодических постоянных платежей в течение заданного числа периодов начисления сложных процентов при фиксированной процентной ставке и заданной текущей стоимости |
|
||||||||||
|
irr(ν [, guess]) |
Возвращает норму прибыли внутри страны для последовательности денежных потоков, следующих через равные промежутки времени |
|
||||||||||
|
IsArray(x) |
Возвращает 1, если x — матрица или вектор. Иначе возвращает 0 |
|
||||||||||
|
IsNaN(x) |
Возвращает 1, если x есть NaN. Иначе возвращает 0 |
|
||||||||||
|
Функция |
Описание |
|
||||||||||
|
IsPrime(n) |
Возвращает 1, если n — простое число, иначе возвращает 0. Может быть вычислена только аналитически |
|
||||||||||
|
IsScalar(x) |
Возвращает 1, если x — число. Иначе возвращает 0 |
|
||||||||||
|
IsString(x) |
Возвращает 1, если x — строка. Иначе возвращает 0 |
|
||||||||||
|
iwave(ν) |
Обратное одномерное дискретное вейвлет-преобразование для wave |
|
||||||||||
|
JO (z) |
Возвращает значение в точке z функции Бесселя первого рода нулевого порядка |
|
||||||||||
|
JO.sc(z) |
Возвращает значение в точке z функции Бесселя первого рода нулевого порядка с коэффициентом масштабирования ехр(-|Im(z)|) |
|
||||||||||
|
J1(z) |
Возвращает значение в точке z функции Бесселя первого рода первого порядка |
|
||||||||||
|
J1.sc(z) |
Возвращает значение в точке z функции Бесселя первого рода первого порядка с коэффициентом масштабирования ехр(-|Im(z)|) |
|
||||||||||
|
Jac(n, a, b, x) |
Возвращает значение в точке x полинома Якоби степени n |
|
||||||||||
|
Jacob(F(x),x [, k] ) |
Возвращает якобиан векторной функции f(x) |
|
||||||||||
|
Jn(m, z) |
Возвращает значение в точке z функции Бесселя первого рода m-го порядка |
|
||||||||||
|
Jn.scfm, z) |
Возвращает значение в точке z функции Бесселя первого рода m-го порядка с коэффициентом масштабирования ехр(-|Im(z)I) |
|
||||||||||
|
js(m, z) |
Возвращает значение в точке z сферической функции Бесселя первого рода m-го порядка |
|
||||||||||
|
К0 (z) |
Возвращает значение в точке z модифицированной функции Бесселя второго рода нулевого порядка |
|
||||||||||
|
К0.sc(z) |
Возвращает значение в точке z модифицированной функции Бесселя второго рода нулевого порядка с коэффициентом масштабирования ехр(z) |
|
||||||||||
|
Κ1(z) |
Возвращает значение в точке z модифицированной функции Бесселя второго рода первого порядка |
|
||||||||||
|
Функция |
Описание |
|
||||||||||
|
К1.sc(z) |
Возвращает значение в точке z модифицированной функции Бесселя второго рода первого порядка с коэффициентом масштабирования ехр (ζ) |
|
||||||||||
|
Kn(m, z) |
Возвращает значение в точке z модифицированной функции Бесселя m-го рода первого порядка |
|
||||||||||
|
Kn.sc(m, z) |
Возвращает значение в точке z модифицированной функции Бесселя второго рода m-го порядка с коэффициентом масштабирования ехр(z) |
|
||||||||||
|
kronecker(M, Ν) |
Возвращает произведение Кронекера квадратной матрицы M на квадратную матрицу N |
|
||||||||||
|
Kronecker delta(x, у) (вид в Mathcad-документе: δ(χ, у)) |
Возвращает значение дельта-функции Кронекера от x, у |
|
||||||||||
|
ksmooth(vx, vy, b) |
Возвращает вектор локальных взвешенных средних значений от vy с использованием гауссова ядра с полосой пропускания b |
|
||||||||||
|
kurt(А, В, C, ...) |
Возвращает значение эксцесса данных а, в, с, ... |
|
||||||||||
|
Lag(n, x) |
Возвращает значение полинома Лагерра степени n в точке x |
|
||||||||||
|
LambertW([n],x) |
Возвращает значение W-функции Ламберта |
|
||||||||||
|
Lambert(n, x) |
Возвращает значение n-й ветви W-функции Ламберта |
|
||||||||||
|
last(v)
|
Возвращает номер последнего элемента вектора ν или последней строки массива ν |
|
||||||||||
|
lcm(А, В, C, . . . ) |
Возвращает наименьшее общее кратное а, в, с, ... |
|
||||||||||
|
Leg(n, x) |
Возвращает значение полинома Лежандра степени n в точке x |
|
||||||||||
|
length(v) |
Возвращает количество элементов ν |
|
||||||||||
|
lgsfit(vx, vy, vg) |
Возвращает значения параметров a, b и с кривой вида у=а/(1+b*е^(-с*х)), аппроксимирующей данные vx, vy; вектор vg содержит начальные значения искомых параметров a, b и с |
|
||||||||||
|
line(vx, vy) |
Возвращает значения параметров а, b прямой у=а+bх, аппроксимирующей данные vx, vy |
|
||||||||||
|
|
|
|
||||||||||
|
Функция |
Описание |
|
||||||||||
|
linfit(vx, vy, F) |
Возвращает значения коэффициентов линейной комбинации сглаживающей функции для данные vx, vy. Сглаживающая функция является линейной комбинацией функций, определенных в F |
|
||||||||||
|
linterp(vx, vy, x) |
Возвращает значение в точке x линейной интерполяции данных νx и vy |
|
||||||||||
|
In (z) |
Возвращает значение натурального логарифма z (для комплексного z — главное значение логарифма) |
|
||||||||||
|
Ιn0(z) |
Возвращает значение натурального логарифма z (для комплексного z — главное значение логарифма), с конечным значением в нуле |
|
||||||||||
|
lnfit(vx, vy) |
Возвращает значения параметров а и b сглаживающей функции вида a*ln(х)+b для данных vx, vy |
|
||||||||||
|
InGamma(z) |
Возвращает значение в точке z натурального логарифма гамма-функции Эйлера |
|
||||||||||
|
LoadColormap(file) |
Возвращает массив, содержащий значения из файла карты цветов с указанным именем |
|
||||||||||
|
loess (vx, vy, span) |
Возвращает вектор, используемый функцией interp для поиска множества многочленов второго порядка, наилучшим образом приближающих значения данных в векторах или матрицах νx и vy в некоторой окрестности. Размер окрестности задается аргументом span |
|
||||||||||
|
log(z [, b])
|
Возвращает значение десятичного логарифма z (логарифма по основанию b) |
|
||||||||||
|
logfit(vx, vy, vg) |
Возвращает значения параметров a, b и с сглаживающей функции вида а*1п (χ+b) +с для данных vx, vy; вектор vg содержит начальные значения искомых параметров a, b и с |
|
||||||||||
|
logpts(minexp, dec, dnpts) |
Возвращает вектор, содержащий dec декад равномерно размещенных точек, начиная от 10 в степени minexp, в количестве dnpts-точек на декаду |
|
||||||||||
|
logspace(min, max, npts) |
Возвращает вектор из npts-точек, расположенных по логарифмическому закону в диапазоне от min до max |
|
||||||||||
|
Функция |
Описание |
|
||||||||||
|
lookup(z, А, В) |
Ищет в векторе или матрице A заданное значение ζ и возвращает это значение (значения) в той же позиции (позициях), т. е. с теми же номерами строк и столбцов, в другой матрице B. Если возвращается несколько значений, они представляются в виде вектора |
|
||||||||||
|
lsolve(M, ν) |
Возвращает вектор х, дающий решение линейной системы уравнений Μ*x=ν |
|
||||||||||
|
lspline(vx, vy) |
Возвращает вектор коэффициентов интерполяционного кубического сплайна с линейными конечными точками функции, заданной значениями vy в узлах vx. Этот вектор становится первым аргументом функции interp |
|
||||||||||
|
lu(М) |
Возвращает матрицы P, L и U, из LU-разложения матрицы M. |
|
||||||||||
|
match(z, А)
|
Ищет в векторе или матрице A заданное значение z и возвращает индексы его позиций в A |
|
||||||||||
|
matrix(m, n, f) |
Возвращает матрицу m*n, в которой (i, j)-й элемент равен f(i, j) |
|
||||||||||
|
max(А, В, С, . . . ) |
Возвращает наибольшее из значений A, B, C, ... Если какое-либо значение комплексное, возвращает mах(Rе(А, B, С, ...)) + i*max(Im(A, B, C, . . . )) |
|
||||||||||
|
Maximize(f, var1, var2, ...)
|
Возвращает значения переменных var1, var2, … приводящие к максимальному значению функции f (и удовлетворяющие ограничениям в блоке Given/Maximaze). Возвращает скаляр, если задан один аргумент, иначе возвращает вектор. Требует первого приближения значений переменных var1, var2,.... Щелкните правой кнопкой мыши по имени этой функции для выбора численного метода решения |
|
||||||||||
|
mean(A, В, С, ...) |
Возвращает среднее арифметическое значение А, В, С, ... |
|
||||||||||
|
medfit(vx, vy) |
Возвращает значения коэффициентов а, b линии медиан-медианной регрессии вида у=а+bх для данных νx и vy |
|
||||||||||
|
median(А, В, С, ...) |
Возвращает медиану данных A, B, C ... |
|
||||||||||
|
|
|
|
||||||||||
|
Функция |
Описание |
|
||||||||||
|
medsmooth(vy, n) |
Возвращает сглаженный вектор, заменяя каждое значение в vy медианой n точек с центром на этом значении |
|
||||||||||
|
mhyper(a, b, x) |
Возвращает значение в точке x вырожденной гипергеометрической функции M(а, b, х) |
|
||||||||||
|
min(A, В, С, . . . ) |
Возвращает наименьшее из значений A, B, C,... Если какое-либо значение комплексное, возвращает min(Re(А, В, С,...)) + i*min(Im(A, В, С, . . .)) |
|
||||||||||
|
Minerr(var1, var2 , . . .) |
Возвращает значения переменных var1, var2, …. наиболее удовлетворяющие системе уравнений и ограничениям в блоке решения. Возвращает скаляр, если задан один аргумент, иначе возвращает вектор. Если решение не сходится, то в отличие от функции Find возвращаются результаты последней итерации. Требует первого приближения значений переменных var1, var2, ... Щелкните правой кнопкой мыши по имени этой функции для выбора численного метода решения |
|
||||||||||
|
Minimize(f, varl, var2, . .)
|
Возвращает значения переменных var1, var2,..., приводящие к минимальному значению функции f (и удовлетворяющие ограничениям в блоке Given/Maximaze). Возвращает скаляр, если задан один аргумент, иначе возвращает вектор. Требует первого приближения значений переменных var1, var2, ... Щелкните правой кнопкой мыши по имени этой функции для выбора численного метода решения |
|
||||||||||
|
mirr(v, fin_rate, rein_rate) |
Возвращает модифицированную норму прибыли внутри страны для вектора денежных потоков ν при заданных стоимости кредита и ставке реинвестирования |
|
||||||||||
|
mod(x, у) |
Возвращает частное от деления x на у (x по модулю y). Знак результата совпадает со знаком x |
|
||||||||||
|
mode(А, В, С, ...) |
Возвращает наиболее часто встречающееся из значений А, B, C, ... |
|
||||||||||
|
multigrid(M, ncycle) |
Возвращает квадратную матрицу значений решения однородной граничной задачи для уравнения Пуассона; ncycle — количество итераций |
|
||||||||||
|
nom(APR, npery) |
Возвращает номинальную процентную ставку при заданных действующей годовой процентной ставке (apr) и числе периодов начисления сложных процентов за год |
|
||||||||||
|
Функция |
Описание |
|
||||||||||
|
Norm1(Μ) |
Возвращает норму L1 квадратной матрицы M |
|
||||||||||
|
norm2(Μ) |
Возвращает норму L2 квадратной матрицы M |
|
||||||||||
|
norme(Μ) |
Возвращает евклидову норму квадратной матрицы M |
|
||||||||||
|
normi(Μ) |
Возвращает бесконечную норму квадратной матрицы M |
|
||||||||||
|
nper(rate, pmt, pv [ [, fv] [, type]]) |
Возвращает число периодов начисления сложных процентов для вклада или ссуды при условии периодических постоянных платежей с использованием фиксированной процентной ставки и указанной текущей стоимости |
|
||||||||||
|
npv(rate, v) |
Возвращает чистую приведенную стоимость вклада при заданных учетной ставке и последовательности денежных потоков, следующих через равные промежутки времени |
|
||||||||||
|
num2str(z) |
Возвращает число z в строку |
|
||||||||||
|
numer(x) |
Возвращает числитель рационального выражения х. Может быть вычислена только аналитически |
|
||||||||||
|
numol(x_endpts, xpts, t_endpts, tpts, num_pde, num_pae, pde_func, pinit, bc_func) |
Возвращает xpts*tpts матрицу, содержащую значения решения задачи Дирихле или задачи Неймана для одномерного уравнения в частных производных, определенной в pde, func. Каждый столбец матрицы представляет значения решения на одномерной сетке в определенный момент времени. Размерность матрицы решения для системы уравнений xpts*(tpts* (num_pde+num_pae)), т. к. значения очередной функции дописываются справа |
|
||||||||||
|
Odesolve([vf,] x, b [, step])
|
Возвращает значение по переменной x решение задачи Коши для дифференциального уравнения (системы), описанного в блоке решения “Given”. При решении системы параметр vf содержит имена искомых функций |
|
||||||||||
|
pause(S, x, y, z, . . . ) |
Возвращает строку, содержащую значения аргументов х, у, z,... с указанием очередности печати и сопровождающим текстом, заданным параметром S. Отображает значения в окне трассировки и приостанавливает выполнение при включенном режиме отладки. Параметр S необязателен, если печатается только одно значение |
|
||||||||||
|
Функция |
Описание |
|
||||||||||
|
pbeta(x, s1, s2) |
Возвращает значение в точке x функции распределения для бета-распределения |
|
||||||||||
|
pbinom(k, n, q) |
Возвращает значение в точке x функции распределения для биномиального распределения |
|
||||||||||
|
pcauchy(x, l, s) |
Возвращает значение в точке x функции распределения для распределения Коши |
|
||||||||||
|
pchisq(x, d) |
Возвращает значение в точке x функции распределения для распределения хи-квадрат |
|
||||||||||
|
Pdesolve(u, x, xrange, t, trange [, xpts] [, tpts]) |
Возвращает значение в точке (х, t) решения граничной задачи для дифференциального уравнения в частных производных, определенного в блоке решения, в прямоугольнике, описанном в xrange, trange |
|
||||||||||
|
permut(n, k) |
Возвращает значение числа размещений из n по к |
|
||||||||||
|
pexp(x, r) |
Возвращает значение в точке x функции распределения для экспоненциального распределения |
|
||||||||||
|
pF(x, d1, d2) |
Возвращает значение в точке x функции распределения для распределения Фишера |
|
||||||||||
|
pgainma (x, s) |
Возвращает значение в точке x функции распределения для гамма-распределения |
|
||||||||||
|
pgeom(k, p) |
Возвращает значение в точке x функции распределения для геометрического распределения |
|
||||||||||
|
phypergeom(m, a, b, n) |
Возвращает значение в точке x функции распределения для гипергеометрического распределения |
|
||||||||||
|
plnorm(x, mu, sigma) |
Возвращает значение в точке x функции распределения для логнормального распределения |
|
||||||||||
|
plogis(χ, l, s) |
Возвращает значение в точке x функции распределения для логистического распределения |
|
||||||||||
|
pmt(rate, nper, pv [, [fv] [, type]]) |
Возвращает выплату по вкладу или ссуде при условии периодических постоянных платежей в течение заданного числа периодов начисления сложных процентов с использованием фиксированной процентной ставки и указанной текущей стоимости |
|
||||||||||
|
pnbinom(k, n, p) |
Возвращает значение в точке x функции распределения для биномиального распределения |
|
||||||||||
|
pnorm(x, mu, sigma) |
Возвращает значение в точке x функции распределения для нормального распределения |
|
||||||||||
|
Функция |
Описание |
|
||||||||||
|
pol2xy(r, theta) |
Возвращает значения прямоугольных координат точки плоскости с заданными полярными координатами |
|
||||||||||
|
polyhedron(S) |
Строит трехмерное изображение правильного многогранника, код или символ Витгофа которого определен в строке S |
|
||||||||||
|
polyLookup(n) |
Возвращает вектор, содержащий имя, второе имя и символ Витгофа для многогранника с кодом n |
|
||||||||||
|
polyroots(ν) |
Возвращает вектор, содержащий все корни многочлена, коэффициенты которого заданы в ν |
|
||||||||||
|
ppmt(rate, per, nper, pv [, [fv] [, type]]) |
Возвращает платеж по основной сумме вклада или ссуды для заданного периода при условии периодических постоянных платежей в течение заданного числа периодов начисления сложных процентов с использованием фиксированной процентной ставки и указанной текущей стоимости |
|
||||||||||
|
ppois(k, l) |
Возвращает значение в точке x функции распределения для распределения Пуассона |
|
||||||||||
|
predict(v, m, n) |
Возвращает прогноз в n точках, построенный по данным ν с использованием коэффициентов автокорреляции m точек в скользящем окне |
|
||||||||||
|
psi(z) |
Возвращает значение в точке z вырожденной дигамма-функции |
|
||||||||||
|
pspline(vx, vy) |
Возвращает вектор коэффициентов кубического сплайна с параболическим граничным условием для данных vx, vy. Этот вектор становится первым аргументом функции interp |
|
||||||||||
|
pt(x, d) |
Возвращает значение в точке x функции распределения для распределения Стьюдента |
|
||||||||||
|
punif(x, a, b) |
Возвращает значение в точке x функции распределения для равномерного распределения |
|
||||||||||
|
pv(rate, nper, pmt [, [fv] [, type]]) |
Возвращает текущую стоимость вклада или ссуды при условии периодических постоянных платежей в течение заданного числа периодов начисления сложных процентов с использованием фиксированной процентной ставки и указанного платежа |
|
||||||||||
|
pweibull(x, s) |
Возвращает значение в точке x функции распределения для распределения Вейбулла |
|
||||||||||
|
Функция |
Описание |
|
||||||||||
|
pwrfit(vx, vy, vg) |
Возвращает значения коэффициентов а, b и с функции мощности вида а*хb+с, которая наилучшим образом аппроксимирует данные в векторах vx и vy. Вектор vg содержит начальные приближения коэффициентов |
|
||||||||||
|
qbeta(p, s1, s2) |
Возвращает квантиль уровня p бета-распределения |
|
||||||||||
|
qbinom(p, n, q) |
Возвращает квантиль уровня p биномиального распределения |
|
||||||||||
|
qcauchy(p, l, s) |
Возвращает квантиль уровня p распределения Коши |
|
||||||||||
|
qchisq(p, d) |
Возвращает квантиль уровня p распределения Коши |
|
||||||||||
|
qexp(p, r) |
Возвращает квантиль уровня p χ-распределения |
|
||||||||||
|
qF(p, d1, d2) |
Возвращает квантиль уровня p распределения Фишера |
|
||||||||||
|
qgamma(p, s) |
Возвращает квантиль уровня p гамма- распределения |
|
||||||||||
|
qgeom(p, q) |
Возвращает квантиль уровня p геометрического распределения |
|
||||||||||
|
qhypergeom(p, a, b, n) |
Возвращает квантиль уровня p гипергеометрического распределения |
|
||||||||||
|
qlnorm(p, mu, sigma) |
Возвращает квантиль уровня p логнормального распределения |
|
||||||||||
|
qlogis(p, l, s) |
Возвращает квантиль уровня p логистического распределения |
|
||||||||||
|
qnbinom(p, n, q) |
Возвращает квантиль уровня p отрицательного биномиального распределения |
|
||||||||||
|
qnorm(p, mu, sigma) |
Возвращает квантиль уровня p нормального распределения |
|
||||||||||
|
qpois(ρ, l) |
Возвращает квантиль уровня p распределения Пуассона |
|
||||||||||
|
qr (A) |
Возвращает матрицу, первые n столбцов которой содержат квадратную ортонормированную матрицу Q, а остальные столбцы содержат верхнюю треугольную матрицу R из QR-разложения матрицы А |
|
||||||||||
|
qt(p, d) |
Возвращает квантиль уровня p распределения Стьюдента |
|
||||||||||
|
Функция |
Описание |
|
||||||||||
|
qunif(p, а, b) |
Возвращает квантиль уровня p равномерного распределения |
|
||||||||||
|
qweibull(p, s) |
Возвращает квантиль уровня p распределения Вей-булла |
|
||||||||||
|
Radau(y, x1, x2 , npoints, D [, J] [, M] [, tol]) |
Возвращает матрицу значений решения задачи Коши жесткой нормальной системы дифференциальных уравнений с правыми частями из D и начальными условиями у в x1. Решение в npoints точках на [x1,x2] вычислено с использованием метода RADAUS |
|
||||||||||
|
rank(A) |
Возвращает ранг матрицы А |
|
||||||||||
|
rate (nper, pint, pv [ [, fv] t, type] [, guess]] ) |
Возвращает процентную ставку за период по вкладу или ссуде в течение заданного числа периодов начисления сложных процентов при заданном периодическом постоянном платеже и указанной текущей стоимости |
|
||||||||||
|
rbeta(m, si, s2) |
Возвращает выбору объема m случайных чисел, имеющих бета-распределение |
|
||||||||||
|
rbinomfm, n, q) |
Возвращает выбору объема m случайных чисел, имеющих биномиальное распределение |
|
||||||||||
|
rcauchy(m, 1, s) |
Возвращает выбору объема m случайных чисел, имеющих распределение Коши |
|
||||||||||
|
rchisq(m, d) |
Возвращает выбору объема m случайных чисел, имеющих распределение χ 2 |
|
||||||||||
|
Re (z) |
Возвращает вещественную часть z |
|
||||||||||
|
READ_BLUE(file) |
Матрица, представляющая синий (B) компонент пространства RGB цветного изображения формата BMP, GIF, JPG или TGA в файле |
|
||||||||||
|
READ_GREEN(file) |
Матрица, представляющая зеленый (G) компонент пространства RGB цветного изображения формата BMP, GIF, JPG или TGA в файле |
|
||||||||||
|
READ_HLS(file) |
Возвращает упакованную матрицу компонентов цветового тона (H), яркости (L) и насыщенности (S) по цветовой модели Оствальда для цветного изображения формата BMP, GIF, JPG или TGA в файле. Возвращаемая матрица содержит матрицы H, L и S, упакованные "бок о бок" |
|
||||||||||
|
Функция |
Описание |
|
||||||||||
|
READ_HL S_HUE(file) |
Матрица, представляющая значения цветового тона пространства HLS (тон-яркость-насыщенность) по цветовой модели Оствальда для цветного изображения формата BMP, GIF, JPG или TGA в файле |
|
||||||||||
|
READ_HLS_LIGHT(file) |
Матрица, представляющая значения компонента яркости пространства HLS (тон-яркость-насыщенность) по цветовой модели Оствальда для цветного изображения формата BMP, GIF, JPG или TGA в файле |
|
||||||||||
|
READ_HLS_SAT(file) |
Матрица, представляющая значения компонента насыщенности пространства HLS (тон-яркость- насыщенность) по цветовой модели Оствальда для цветного изображения формата BMP, GIF, JPG или TGA в файле |
|
||||||||||
|
READ_HSV(file) |
Упакованная матрица компонентов цветового тона (H), насыщенности (S) и значения (V) по цветовой модели HSV Смита для цветного изображения формата BMP, GIF, JPG или TGA в файле. Возвращаемая матрица содержит матрицы H, S и V, упакованные "бок о бок" |
|
||||||||||
|
READ_HSV_HUE(file) |
Матрица, представляющая значения цветового тона пространства HSV (тон-насыщеность-значение) по цветовой модели HSV Смита для цветного изображения формата BMP, GIF, JPG или TGA в файле |
|
||||||||||
|
READ_HSV_SAT(file) |
Матрица, представляющая значения компонента насыщенности пространства HSV (тон-насыщеность-значение) по цветовой модели HSV Смита для цветного изображения формата BMP, GIF, JPG или TGA в файле |
|
||||||||||
|
READ_HSV_VALUE(file) |
Матрица, представляющая компоненты значения пространства HSV (тон-насыщеность-значение) по цветовой модели HSV Смита для цветного изображения формата BMP, GIF, JPG или TGA в файле |
|
||||||||||
|
READ_IMAGE(file) |
Возвращает матрицу, содержащую представление оттенков серого для изображения формата BMP, GIF, JPG или TGA в файле |
|
||||||||||
|
READ_RED(file) |
Матрица, представляющая красный (R) компонент пространства RGB изображения формата BMP, GIF, JPG или TGA в файле |
|
||||||||||
|
READBIN(file, type [, [endian] [, cols] [, skip] [, maxrows]]) |
Возвращает матрицу из файла двоичных данных единого формата с указанным типом файла |
|
||||||||||
|
Функция |
Описание |
|
||||||||||
|
READBMP(file) |
Возвращает массив целых чисел от 0 (черный) до 255 (белый), представляющий оттенки серого изображения формата BMP в файле |
|
||||||||||
|
READFILE(file, type [, [colwidths] t, rows] [, cols] [, emptyfill]]) |
Возвращает матрицу из содержимого файла указанного типа (с разделителями, с фиксированной шириной или формата Excel) |
|
||||||||||
|
READPRN(file) |
Возвращает матрицу, полученную из файла со структурированными данными в используемой файловой системе |
|
||||||||||
|
READRGB(file) |
Возвращает упакованную матрицу из красного (R), зеленого (G) и синего (В) компонентов пространства RGB для цветного изображения формата BMP в файле. Возвращаемая матрица содержит матрицы R, G и В, упакованные "бок о бок" |
|
||||||||||
|
READWAV(file) |
Создает матрицу, содержащую амплитуды сигналов из файла. Каждый столбец представляет отдельный канал данных. Каждая строка соответствует определенному моменту времени |
|
||||||||||
|
regress(vx, vy, n) |
Возвращает коэффициенты для множественной регрессии, для зависимости, заданной значениями vy в n-мерных точках vx |
|
||||||||||
|
relax(A, В, C, D, E, F, U, rjac) |
Возвращает квадратную матрицу значений решения граничной задачи для уравнения Пуассона с граничными условиями, заданными в U, A, B, C, D и E задают коэффициенты разностной аппроксимации лапласиана |
|
||||||||||
|
reverse(A) |
Возвращает матрицу (вектор) переставленных в обратном порядке строк матрицы A (элементов вектора) |
|
||||||||||
|
rexp(m, r) |
Возвращает выборку объема m случайных чисел, имеющих экспоненциальное распределение |
|
||||||||||
|
rF(m, d1, d2) |
Возвращает выбору объема m случайных чисел, имеющих распределение Фишера |
|
||||||||||
|
rgamma(m, s) |
Возвращает выбору объема m случайных чисел, имеющих гамма-распределение |
|
||||||||||
|
rgeom(m, q) |
Возвращает выбору объема m случайных чисел, имеющих геометрическое распределение |
|
||||||||||
|
rhypergeom(m, a, b, n) |
Возвращает выбору объема m случайных чисел, имеющих гипергеометрическое распределение |
|
||||||||||
|
|
|
|
||||||||||
|
Функция |
Описание |
|
||||||||||
|
Rkadaptty, xl, х2, npoints, D) |
Возвращает матрицу значений решения задачи Коши нормальной системы дифференциальных уравнений, с правыми частями из D и начальными условиями у в x1. Решение в npoints-точках на [x1,x2] вычислено методом Рунге — Кутты с автоматическим выбором шага |
|
||||||||||
|
rkfixedfy, xl, x2, npoints, D) |
Возвращает матрицу значений решения задачи Коши нормальной системы дифференциальных уравнений с правыми частями из D и начальными условиями у в x1. Решение в npoints-точках на [x1, х2] вычислено методом Рунге — Кутты с постоянным шагом |
|
||||||||||
|
rlnorm(m, mu, sigma) |
Возвращает выбору объема m случайных чисел, имеющих логнормальное распределение |
|
||||||||||
|
rlogis(m, l, s) |
Возвращает выбору объема m случайных чисел, имеющих логистическое распределение |
|
||||||||||
|
rnbinom(m, n, p) |
Возвращает выбору объема m случайных чисел, имеющих отрицательное биномиальное распределение |
|
||||||||||
|
rnd(x) |
Возвращает случайное число, равномерно распределенное на [0, х] |
|
||||||||||
|
Rnorm(m, mu, sigma) |
Возвращает объем m случайных чисел, имеющих нормальное распределение |
|
||||||||||
|
root(f(var), var [, a, b]) |
Возвращает решение уравнения f (var) =0 на отрезке [a, b]; root(f(var),var) возвращает решение, начальное приближение которого предварительно присвоено переменной var |
|
||||||||||
|
Round(z, у) |
Округляет z до ближайшего кратного у, обычно используется для правильного масштабирования единицы измерения |
|
||||||||||
|
round(z, n) |
Округляет z до n разрядов. Если n опущено, z округляется до ближайшего целого. Если n < 0, z округляется влево от десятичного разделителя |
|
||||||||||
|
rows(A)
|
Возвращает число строк в массиве а |
|
||||||||||
|
rpois(m, l) |
Возвращает выбору объема m случайных чисел, имеющих распределение Пуассона |
|
||||||||||
|
rref(A) |
Возвращает ступенчатую форму матрицы A, вычисленную Гауссовым исключением |
|
||||||||||
|
Функция |
Описание |
|
||||||||||
|
rsort(A, n) |
Возвращает матрицу, полученную такой перестановкой столбцов в массиве А, при которой элементы n-й строки а упорядочены по возрастанию |
|
||||||||||
|
rt(m, d) |
Возвращает выбору объема m случайных чисел, имеющих распределение Стьюдента |
|
||||||||||
|
runif(m, a, b |
Возвращает выбору объема m случайных чисел, имеющих равномерное распределение |
|
||||||||||
|
rweibull(m, s) |
Возвращает выбору объема m случайных чисел, имеющих распределение Вейбулла |
|
||||||||||
|
SaveColormap(file, M) |
Создает файл карты цветов с указанным именем, содержащий значения из матрицы M. Возвращает число строк, записанных в файл |
|
||||||||||
|
sbval(v, x1, x2, D, load, score) |
Возвращает набор начальных условий для граничной задачи, заданной производными в D и начальными приближениями ν на интервале [x1, х2]. Параметр load содержит и известные начальные условия, и начальные приближения из ν, а параметр score измеряет расхождение решения в х2 |
|
||||||||||
|
search(S1, SubS, m) |
Возвращает начальную позицию подстроки SubS в S1, считая с позиции m |
|
||||||||||
|
sec(z) |
Возвращает значение секанса в точке z |
|
||||||||||
|
sech(z) |
Возвращает значение гиперболического секанса в точке z |
|
||||||||||
|
Seed(x) |
Сбрасывает начальное значение случайного числа в x и возвращает предыдущее значение |
|
||||||||||
|
Shi(x) |
Возвращает значение интегрального гиперболического синуса в точке x |
|
||||||||||
|
Si (x) |
Возвращает значение интегрального синуса в точке x |
|
||||||||||
|
sign(x) |
Возвращает 0, если x = 0; возвращает 1, если x > 0; иначе возвращает -1, если x < 0; x — действительное число |
|
||||||||||
|
Signum(z [, x]) |
Возвращает х, если z = 0, иначе возвращает z / | z | |
|
||||||||||
|
sin(z)
|
Возвращает значение синуса в точке z |
|
||||||||||
|
|
|
|
||||||||||
|
Функция |
Описание |
|
||||||||||
|
sinc(z) |
Возвращает значение sin(z)/z с корректным вычислением вблизи нуля |
|
||||||||||
|
sinfit(vx, vy, vg) |
Возвращает значения коэффициентов а, b и с, функции вида a*sin(x+b)+с, аппроксимирующей функцию, заданную значениями vy в точках νx; вектор vg содержит начальные приближения коэффициентов a, b и с |
|
||||||||||
|
sinh(z) |
Возвращает значение гиперболического синуса в точке z |
|
||||||||||
|
SlUnitsOf(x) |
Возвращает единицы измерения х. Если аргумент x не имеет единиц измерения, возвращает 1 |
|
||||||||||
|
skew(А, В, С, ...) |
Возвращает значение коэффициента асимметрии данных А, B, C,... |
|
||||||||||
|
slope(vx, vy) |
Возвращает значение коэффициента а линейной функции у=а*х+b, аппроксимирующей данные νx и vy |
|
||||||||||
|
sort(v) |
Возвращает вектор, содержащий упорядоченные по возрастанию элементы ν |
|
||||||||||
|
sph2xyz(r, theta, phi) |
Возвращает прямоугольные координаты точки пространства, заданной сферическими координатами |
|
||||||||||
|
stack(А, В, C, ...) |
Возвращает массив, полученный в результате размещения скаляров или массивов А, B, C,... сверху вниз. Если А, B, C,... — массивы, то они должны иметь одинаковое число столбцов |
|
||||||||||
|
statespace(init, t1, t2,npoints, A [, B] [, u]) |
Возвращает значения решения x(t) задачи Коши для линейной системы первого порядка х' =А*х+b*u; начальные условия в t1 заданы в init; решение вычисляется на [t1, t2] в npoints-точках |
|
||||||||||
|
stderr(vx, vy) |
Возвращает значение среднеквадратичной ошибки линейной регрессии, построенной по данным vx, vy |
|
||||||||||
|
Stdev(А, В, C, ...) |
Возвращает значение квадратного корня из смещенной точечной оценки дисперсии выборки А, B, C,... |
|
||||||||||
|
stdev(А, В, C, ...) |
Возвращает значение квадратного корня из несмещен- ной точечной оценки дисперсии выборки А, B, C,... |
|
||||||||||
|
Функция |
Описание |
|
||||||||||
|
Stiffb(у, x1, х2, npoints, D, AJ) |
Возвращает матрицу значений решения задачи Коши жесткой нормальной системы дифференциальных уравнений, с правыми частями из d, якобианом AJ и начальными условиями у в x1. Решение в npoints-точках на [x1,x2], вычислено методом Булирша — Штера (b) |
|
||||||||||
|
Stiffr(y, xl, x2 , npoints, D, AJ) |
Возвращает матрицу значений решения задачи Коши жесткой нормальной системы дифференциальных уравнений, с правыми частями из d и начальными условиями у в x1. Решение в npoints-точках на [x1,х2] вычислено методом Розенброка(r) |
|
||||||||||
|
str2num(S) |
Возвращает константу, образованную преобразованием строки S в число |
|
||||||||||
|
str2vec(S) |
Возвращает вектор кодов ASCII, соответствующих символам строки S |
|
||||||||||
|
strlen(S) |
Возвращает число символов в строке S |
|
||||||||||
|
submatrix(A, ir, jr, ic, jc)
|
Возвращает подматрицу массива A, состоящую из элементов строк от ir до jr и столбцов от ic до jc массива A |
|
||||||||||
|
substr(S, m, n) |
Возвращает подстроку S, начинающуюся с m-го символа и имеющую максимальную длину n |
|
||||||||||
|
supsmooth(vx, vy) |
Возвращает вектор значений, сглаживающих данные vy , вычисленный симметричным линейным сглаживанием по ближайшим соседям методом наименьших квадратов с адаптивным выбором числа ближайших соседей |
|
||||||||||
|
svd2(A) |
Возвращает массив, содержащий матрицы U, S, V SVD-разложения матрицы A |
|
||||||||||
|
tan(z) |
Возвращает тангенс z |
|
||||||||||
|
tanh(z) |
Возвращает гиперболический тангенс z |
|
||||||||||
|
Tcheb(n, x) |
Возвращает значение полинома Чебышева степени n первого рода в точке x |
|
||||||||||
|
time(z)
|
Возвращает текущее системное время в секундах. Значение z — произвольное выражение Mathcad, не влияющее на возвращаемое значение |
|
||||||||||
|
tr(Μ) |
Возвращает след квадратной матрицы M |
|
||||||||||
|
|
|
|
||||||||||
|
Функция |
Описание |
|
||||||||||
|
trace(S, x, у, z, . . . ) |
Возвращает строку, содержащую значения аргументов х, у, z, ... с указанием очередности печати и сопровождающим текстом, заданным параметром S. Отображает значения в окне трассировки при включенном режиме отладки. Параметр S необязателен, если печатается только одно значение |
|
||||||||||
|
Trunc(z,у) |
Возвращает значение trunc (z/у)*у, обычно используемое для правильного масштабирования единицы измерения |
|
||||||||||
|
trunc(z) |
Возвращает целую часть z, удаляя дробную часть |
|
||||||||||
|
Ucheb(n, x) |
Возвращает значение полинома Чебышева степени n второго рода в точке x |
|
||||||||||
|
until(icond, x) |
Возвращает x до тех пор, пока icond остается отрицательным |
|
||||||||||
|
Var(а, в, с, ...) |
Возвращает значение несмещенной точечной оценки дисперсии выборки а, в, с, ... |
|
||||||||||
|
var(А,В,С, . . . ) |
Возвращает значение смещенной точечной оценки дисперсии выборки а, в, с, ... |
|
||||||||||
|
vec2str(ν) |
Возвращает строку, содержащую элементы вектора ν, преобразованные из кодов ASCII в символы |
|
||||||||||
|
vlookup(z, А, c) |
Выполняет поиск в первом столбце матрицы а заданного значения z. Найденные значения возвращаются в тех же строках в заданном столбце c. Если возвращается несколько значений, они представлены вектором |
|
||||||||||
|
wave(ν) |
Возвращает значения коэффициентов вейвлет- преобразования вектора ν, вычисленные с использованием 4-коэффициентного вейвлет-фильтра Добеши |
|
||||||||||
|
WRITE_HLS(file) |
Записывает упакованную матрицу, состоящую из компонентов цветового тона, яркости и насыщенности изображения, в файл цветного изображения формата BMP Windows с 16 млн. цветов в текущей файловой системе |
|
||||||||||
|
WRITE_HSV(file) |
Записывает упакованную матрицу, состоящую из компонентов цветового тона, насыщенности и значения изображения, в файл цветного изображения формата BMP Windows с 16 млн. цветов в текущей файловой системе |
|
||||||||||
|
Функция |
Описание |
|
||||||||||
|
WRITEBIN(file, type, endian) |
Записывает массив скаляров в файл двоичных данных с именем file |
|
||||||||||
|
WRITEBMP(file) |
Записывает массив в BMP-файл оттенков серого в текущей файловой системе |
|
||||||||||
|
WRITEPRN(file) |
Записывает массив в файл в текущей файловой системе |
|
||||||||||
|
WRITERGB(file) |
Записывает упакованную матрицу, состоящую из красного, зеленого и синего компонентов изображения, в файл изображения формата BMP Windows с 16 млн. цветов в текущей файловой системе |
|
||||||||||
|
WRITEWAV(file, s, b) |
Записывает матрицу как файл сигналов формата WAV |
|
||||||||||
|
xy2pol(x, y) |
Возвращает значение полярных координат точки плоскости, заданной прямоугольными координатами |
|
||||||||||
|
xyz2cyl(x, y, z) |
Возвращает значение цилиндрических координат точки пространства, заданной прямоугольными координатами |
|
||||||||||
|
xyz2sph(x, y, z) |
Возвращает значение сферических координат точки пространства, заданной прямоугольными координатами |
|
||||||||||
|
YO(z) |
Возвращает значение в точке z функции Бесселя второго рода нулевого порядка |
|
||||||||||
|
YO.sc(z) |
Возвращает значение в точке z функции Бесселя второго рода нулевого порядка с коэффициентом масштабирования ехр(- |Im(z)|) |
|
||||||||||
|
Y1(z) |
Возвращает значение в точке z функции Бесселя второго рода первого порядка |
|
||||||||||
|
Yl.sc(z) |
Возвращает значение в точке z функции Бесселя второго рода первого порядка с коэффициентом масштабирования ехр(- |Im(z)|) |
|
||||||||||
|
Yn(m,z) |
Возвращает значение в точке z функции Бесселя второго рода m-го порядка |
|
||||||||||
|
Yn.sc(m, z) |
Возвращает значение в точке z функции Бесселя второго рода m-го порядка с коэффициентом масштабирования ехр(- |Im(z)|) |
|
||||||||||
|
ys(m,z) |
Возвращает значение в точке z сферической функции Бесселя второго рода m-го порядка |
|
||||||||||
|
Zeta(s) |
Возвращает значение в точке s дзета-функции Ри-мана. Может быть вычислена только аналитически |
|
||||||||||
назад
Литература
Адлер Ю.П., Маркова Е.В. и др. Планирование эксперимента при поиске оптимальных условий. — М.: Наука, 1971;
Аллен Р. Математическая экономика. — М.: Иностранная литература, 1963;
Большев Л.Н., Смирнов H.В. Таблицы математической статистики. — М.: Наука, 1983
Варфоломеев В.И. «Алгоритмическое моделирование элементов экономических систем»;
Высшая математика для экономистов: Учебное пособие/Под ред. Н.Ш. Кремера;
Глухов В.В., Лисочкина Т.В. и др. Экономические основы экологии: Учебник. — М.: Высшая школа, 1994;
Гринин А.С., Орехов Н.А., Новиков В.Н. «Математическое моделирование в экологии»;
Гриценко А.И., Акопова Г.С., Максимов В.М. «Экология. Нефть и газ.»;
Гулямов С.С., Аимбетов H.К и др. Формирование и развитие промышленных узлов в Каракалпакстане. — Нукус.: Каракалпак- стан, 1993;
Ерофеев Б.В. Экологическое право России. — М.: МНЭПУ, I 995;
Иванилов Ю.П., Лотов А.В. Математические модели в экономике. — М.: Наука, 1979;
Крамер Г. Математические методы статистики. — М.: Мир, 1975;
Лакин Г.Ф. Биометрия. — М.: Высшая школа. 1980. — 293 с.;
Львов Ю.А. Основы экономики и организации бизнеса.— Сиб.: ГМП «Формика», 1992;
Нестеров В.В., Нестеров П.М. Экономика природопользования и охрана природы: Учебник. — М.: Высшая школа, 1994;
Омнигенная экология: Учебное пособие / Под ред. проф. А.С. Гришина. — Калуга: ГУП «Облиздат», 1997;
Реймерс Н.Ф. Надежды на выживание человечества. Концептуальная экология. — М.: Наука, 1992;
Реймерс Н.Ф. Экология (теория, законы, правила, принципы и гипотезы). — М.: Молодая Россия, 1994;
Усманова З.Д. «Моделирование времени»;
Федоров М.П., Романов М.Ф. «Математические основы экологии»;
Франс Дж., Торнели Дж., Математические методы в сельском хозяйстве. — М.: Агропромиздат, 1987;
Химмельблау Д. Анализ процессов статистическими методами: Пер. с англ. — М.: Мир, 1973.
Чверткин Н.С. «Исследоваие и разработка декларации безопасности опасного производственного объекта»;
Шарапов И.П. «Применение математической статистики в геологии»;
Шелобаев С.И. «Математические методы и модели. Экономика. Финансы. Бизнес»;
Шмидхейни С. и др. Смена курса: Пер. с англ. — М.: Геликон, 1994.
Эколого-информационные технологии: Учебное пособие/Под. ред. А.С. Гринина. — Калуга: ГУП «Облиздат», 1999.