ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 31.03.2024
Просмотров: 1068
Скачиваний: 0
СОДЕРЖАНИЕ
Математическое моделирование элементов сложных экологических систем
Лекция 1. Введение в моделирование. Исторический экскурс.
1. Основы моделирования в экологии 1.1. Общие принципы построения моделей в экологии
2.2. Этапы построения математической модели
1.4. Элементы теории подобия, применяемые в моделировании
3.2.2. Выборочный метод в экологометрике.
Зависимость числа интервалов от объема выборки
Статистический ряд по интервалам
Лекция 4. Статистические оценки параметров распределения случайных величин по выборкам
4.4. Статистические оценки гипотез об экологических моделях
Выборка из генеральной совокупности
Статистическая таблица эксперимента
Пример преобразования членов уравнения регрессии
Вычисление данных для линеаризации уравнения регрессии
Нормальные уравнения мнк для некоторых функций
Статистическое оценивание уравнения регрессии и парной корреляции.
Обработка результатов наблюдений
Рекомендации по выбору вида функции
3.4. Динамические статистические модели
Данные по объему сброса качественных сточных вод
Данные по объему сброса сточных вод за 5-летие
Пример расчета 5-летних средних
Расчетные значения для определения уравнения динамики
Ряд динамики для определения сезонных колебаний
Эксперименталъный материал исследования
8.1. Анализ влияния отдельных факторов в экологической модели.
Лекция 9. Методы оптимизации. Метод Лагранжа
Лекция 10. Метод линейного программирования.
Лекция 11. Функциональные модели.
Лекция 12. Модели процессов содержащие обыкновенные дифференциальные уравнения.
Численные ошибки использованных для вычисления данных
Лекция 13. Статистические модели динамики.
Лекция 16. Информационные технологии в экологии. Экологические информационные системы.
1 6.1. Экологические информационные системы
1. Какова область значения для числовых характеристик?
Лекция 17. Использование информационных технологий для решения задач экологии.
Критические значения коэффициента корреляции rk;α
2.1. Подобие физических явлений и его признаки
2.4. Применение методов подобия в математическом
11.3. Численные методы решения дифференциальных уравнений
11.3.2. Процесс численного решения
11.3.4. Модифицированный метод Эйлера
11.3.6. Метод Рунге – Кутта для систем дифференциальных уравнений
11.3.7. Общая характеристика одношаговых методов
11.3.9. Методы прогноза и коррекции
11.3.10. Краткая характеристика методов прогноза и коррекции.
11.3.11. Выбор шага и погрешность решения.
11.4. Имитационное моделирование систем
11.4.1. Принципы имитационного моделирования
11.4.3. Динамическая модель исследуемого объекта
11.4.4. Построение имитационных моделей динамических систем
11.4.5. Преобразование передаточных функций звеньев в дифференциальные уравнения в форме Коши
11.4.6. Синтез имитационной модели на основе структурной схемы
11.5. Теоретические основы построения математических моделей систем
11.5.1. Компонентные и топологические уравнения
11.5.2. Компонентные и топологические уравнения механической системы
11.5.3. Компонентные и топологические уравнения электрической системы
11.5.4. Компонентные и топологические уравнения гидравлической системы
11.5.5. Компонентные и топологические уравнения тепловой системы
11.6.1. Сущность метода электроаналогий.
11.6.2. Электромеханические аналогии
11.6.3. Построение имитационных моделей методом электроаналогий
11.6.4. Плоское прямолинейное движение звеньев
11.6.5. Электрогидравлические аналогии
Index3.html
При абсолютном подобии явлений требуется, чтобы во все сходственные моменты времени во всех сходственных точках пространства переменные и параметры одной системы были пропорциональны соответствующим параметрам другой системы. В общем виде это условие можно записать следующим образом:
![]()
где Pi, Ri - сходственные переменные и параметры элементов рассматриваемых систем; mi - коэффициенты подобия или масштабы сходственных параметров.
2.2. Анализ размерностей
Все упомянутые выше виды подобия подчиняются некоторым общим закономерностям, которые принято называть теоремами о подобии. Этих теорем три [3]. Доказательство данных теорем основано на положении теории размерности. Рассмотрим некоторые из этих положений. Измерение любой физической величины сводится к сравнению ее с некоторой одноименной величиной, принятой за единицу. В результате измерения получается отвлеченное число, выражающее отношение рассматриваемой величины к единице измерения. Если, например, данная величина a , будучи измерена соответствующей единицей измерения [a], дает число {a}, то можно записать
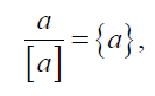
где [a] – единица измерения; {a} – числовое значение величины (безразмерный коэффициент). Измерив ту же величину a единицей [b] = m×[a], получим соответственно
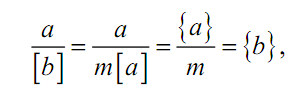
т. е. {a} = m{b}.
Это означает, что при уменьшении или увеличении единицы измерения данной величины в m раз во столько же раз соответственно увеличится или уменьшится число, которым эта величина выражается. Единицы измерения могут быть основными и производными. Совокупность основных единиц и производных, образованных по определенным правилам, составляет систему единиц. Основные единицы характеризуются тем, что размер ее выбирается
произвольно и не зависит от остальных единиц.
Всякая производная единица измерения является степенной функцией от основных единиц измерения. Поскольку формулы размерностей воспроизводят зависимость между самими физическими величинами, то каждая физическая величина может быть выражена через величины, соответствующие основным
единицам измерения, только посредством степенной функции вида:
![]()
где a - данная физическая величина; α, β, κ, γ - отвлеченные числа;
a1,а2, …,аk - физические величины, соответствующие основным единицам измерения.
Например, если в качестве величин, соответствующих основным единицам измерения, принять массу m, длину l и время t, то мощность, как известно, можно выразить через эти величины следующим образом:
![]()
Предположим, что мы пользуемся системой, в основу которой положены k основных единиц, например, a1,а2, …,аk. Тогда производная единица [ak+ 1] является их функцией вида:
![]()
где α1, β1, κ, γ1 – любые действительные числа, называемые размерностями производной единицы [ak+ 1] относительно основных единиц [a1] [а2] […] [ak] .
Уравнение (2.1), дающее зависимость производной единицы от основной единицы, называется формулой размерностей. При переходе к другой системе, в которой основными единицами будут
[b1] [b2] … [bk],
причем
![]() ;
;
![]() ;
……..
;
……..![]()
единица измерения производной величины так же изменится, а именно:
![]() (2.2)
(2.2)
Следовательно,
изменение производной единицы
![]() ,
,
где
![]()
Выражение (2.2) раскрывает основной смысл формулы размерности, показывая как с изменением основных единиц изменяется данная производная единица измерения. При подстановке в (2.1) вместо [a1]; [а2];…..; [аk] величин, им пропорциональных (что аналогично переходу к новой системе единиц), коэффициенты пропорциональности в соответствующих степенях объединяются в один общий множитель 1 N , на который будет умножено первоначальное выражение. Функции, обладающие таким свойством, носят название однородных (гомогенных) функций.
Свойством однородности будут обладать и уравнения,
Q + Q +……+ Q = 0
члены которых составлены из величин, являющихся однородными функциями. Однородность физических уравнений является следствием правила Фурье, согласно которому члены такого уравнения имеют одинаковую размерность, а следовательно, общие множители N1 = N2 = …… = Nn каждого из членов уравнения одинаковы и могут быть вынесены за знак суммы.
2.3. Первая теорема подобия
У явлений, подобных в том или ином смысле (физически или математически), можно найти определенные сочетания параметров, называемые критериями подобия, которые имеют одинаковые значения.
Рассмотрим два процесса, описываемых однородными уравнениями.
Для первого процесса
Q1 + Q2 +……+ Qn = 0. (2.3)
Для второго процесса
q1 + q2 + …… + qn = 0 .4)
где
Qi = fi(P1,P2,….,Pm), i= 1…. n (2.5)
qi = fi(R1,R2,…..,Rm), i = 1…. n
В уравнениях (2.3) и (2.4) Qi и qi - однородные функции. В свою очередь P1 и R1, Р2 и R2 . . . Pm и Rm – сходственные переменные и параметры двух процессов. Поскольку Qn и qn не равны нулю, то уравнения (2.3) и (2.4) можно переписать в виде:
![]()
![]() (2.3а)
(2.3а)
![]() (2.4а)
(2.4а)
Для подобных процессов уравнения (2.3а) и (2.4а) совпадают, т.е. они тождественны. Поскольку процессы подобны, то:
![]() ;
;
![]() ;
……;
;
……;
![]()
или
P1 = m1R1; P2 = m2R2; ……; Pm = mmRm (2.6)
После подстановки в уравнение (2.5) соотношений (2.6) вследствие однородности функции i Q можно вынести масштабы m1,m2, ….., mm в соответствующих степенях за знак функции в виде общего множителя Ni , т. е.
Qi = fi(P1,…..,Pm) = fi(m1R1,….., mmRm)= Ni fi(R1,…..,Rm) = Niqi