ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 31.03.2024
Просмотров: 1108
Скачиваний: 0
СОДЕРЖАНИЕ
Математическое моделирование элементов сложных экологических систем
Лекция 1. Введение в моделирование. Исторический экскурс.
1. Основы моделирования в экологии 1.1. Общие принципы построения моделей в экологии
2.2. Этапы построения математической модели
1.4. Элементы теории подобия, применяемые в моделировании
3.2.2. Выборочный метод в экологометрике.
Зависимость числа интервалов от объема выборки
Статистический ряд по интервалам
Лекция 4. Статистические оценки параметров распределения случайных величин по выборкам
4.4. Статистические оценки гипотез об экологических моделях
Выборка из генеральной совокупности
Статистическая таблица эксперимента
Пример преобразования членов уравнения регрессии
Вычисление данных для линеаризации уравнения регрессии
Нормальные уравнения мнк для некоторых функций
Статистическое оценивание уравнения регрессии и парной корреляции.
Обработка результатов наблюдений
Рекомендации по выбору вида функции
3.4. Динамические статистические модели
Данные по объему сброса качественных сточных вод
Данные по объему сброса сточных вод за 5-летие
Пример расчета 5-летних средних
Расчетные значения для определения уравнения динамики
Ряд динамики для определения сезонных колебаний
Эксперименталъный материал исследования
8.1. Анализ влияния отдельных факторов в экологической модели.
Лекция 9. Методы оптимизации. Метод Лагранжа
Лекция 10. Метод линейного программирования.
Лекция 11. Функциональные модели.
Лекция 12. Модели процессов содержащие обыкновенные дифференциальные уравнения.
Численные ошибки использованных для вычисления данных
Лекция 13. Статистические модели динамики.
Лекция 16. Информационные технологии в экологии. Экологические информационные системы.
1 6.1. Экологические информационные системы
1. Какова область значения для числовых характеристик?
Лекция 17. Использование информационных технологий для решения задач экологии.
Критические значения коэффициента корреляции rk;α
2.1. Подобие физических явлений и его признаки
2.4. Применение методов подобия в математическом
11.3. Численные методы решения дифференциальных уравнений
11.3.2. Процесс численного решения
11.3.4. Модифицированный метод Эйлера
11.3.6. Метод Рунге – Кутта для систем дифференциальных уравнений
11.3.7. Общая характеристика одношаговых методов
11.3.9. Методы прогноза и коррекции
11.3.10. Краткая характеристика методов прогноза и коррекции.
11.3.11. Выбор шага и погрешность решения.
11.4. Имитационное моделирование систем
11.4.1. Принципы имитационного моделирования
11.4.3. Динамическая модель исследуемого объекта
11.4.4. Построение имитационных моделей динамических систем
11.4.5. Преобразование передаточных функций звеньев в дифференциальные уравнения в форме Коши
11.4.6. Синтез имитационной модели на основе структурной схемы
11.5. Теоретические основы построения математических моделей систем
11.5.1. Компонентные и топологические уравнения
11.5.2. Компонентные и топологические уравнения механической системы
11.5.3. Компонентные и топологические уравнения электрической системы
11.5.4. Компонентные и топологические уравнения гидравлической системы
11.5.5. Компонентные и топологические уравнения тепловой системы
11.6.1. Сущность метода электроаналогий.
11.6.2. Электромеханические аналогии
11.6.3. Построение имитационных моделей методом электроаналогий
11.6.4. Плоское прямолинейное движение звеньев
11.6.5. Электрогидравлические аналогии
Лекция 6.
Нелинейный регрессионный анализ
 Если
при
проверке
гипотезы
о
линейности
устанавливается,
что
статистический
материал
не
может
быть
описан
линейным
уравнением,
то
переходят к
поиску
нелинейной
модели.
Если
при
проверке
гипотезы
о
линейности
устанавливается,
что
статистический
материал
не
может
быть
описан
линейным
уравнением,
то
переходят к
поиску
нелинейной
модели.
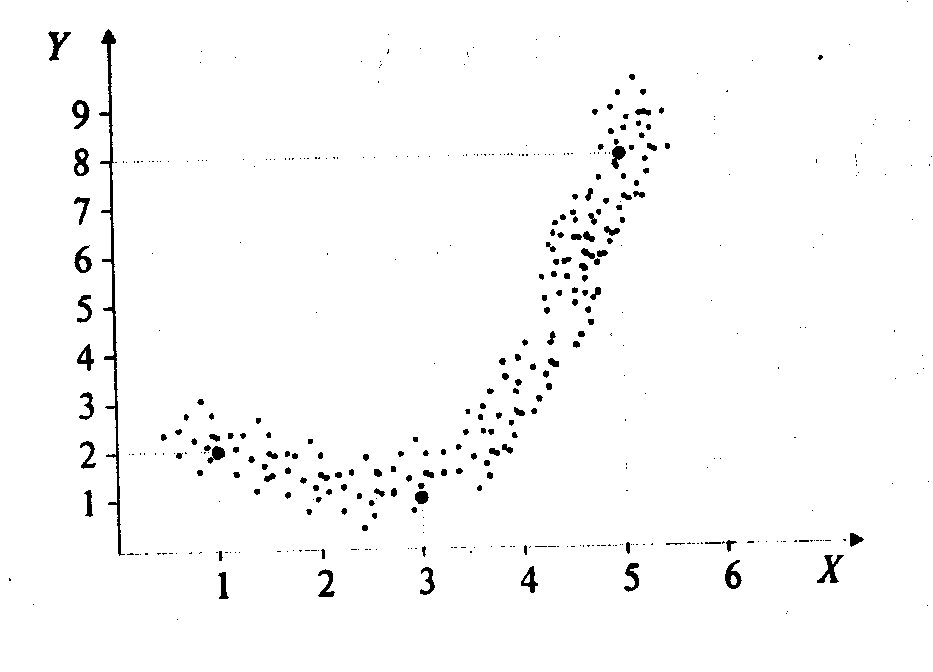
Для предварительного выбора вида модели можно использовать примеры, приведенные в табл. 6.1. Рис.(6.1.) Поле рассеяния.
Можно воспользоваться интерполяцией. Для этого на поле рассеяния (рис.6.1.) следует выбрать несколько характерных точек, например х1= 1, х2= 3, х3= 5, и записать соответствующие пары (х1,у1), (х2,у2) и (x3, y3). Тогда нтерполяционная формула Лагранжа будет иметь вид при уi= 2; уi = 1;
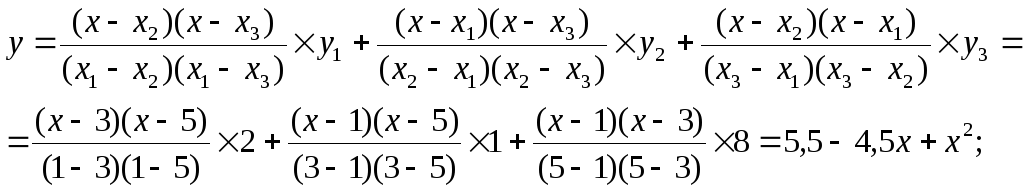
y = 5,5 - 4,5x+х2 .
Таблица (6.1.)
Рекомендации по выбору вида функции
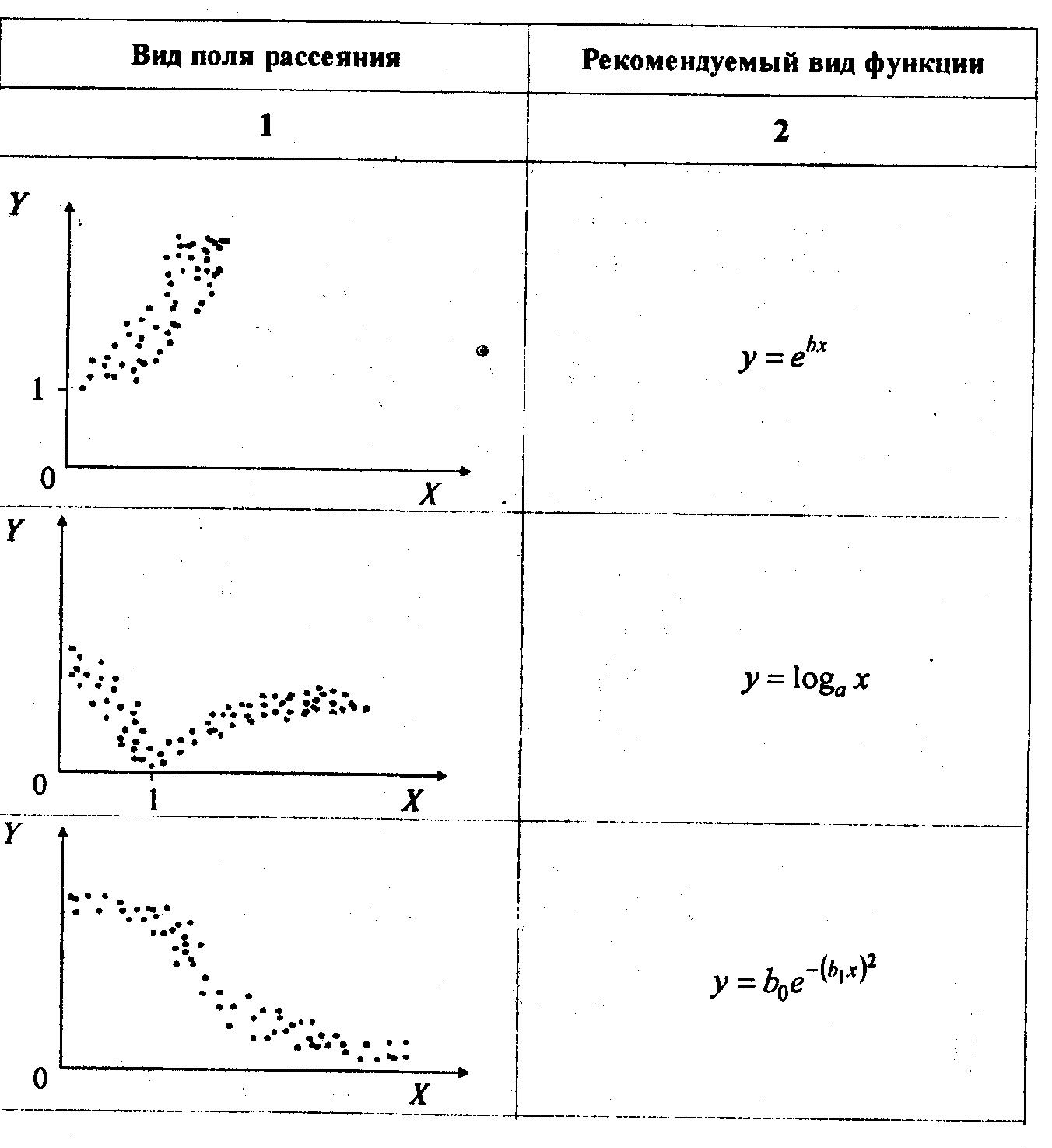
Продолжение табл. 6. 1.
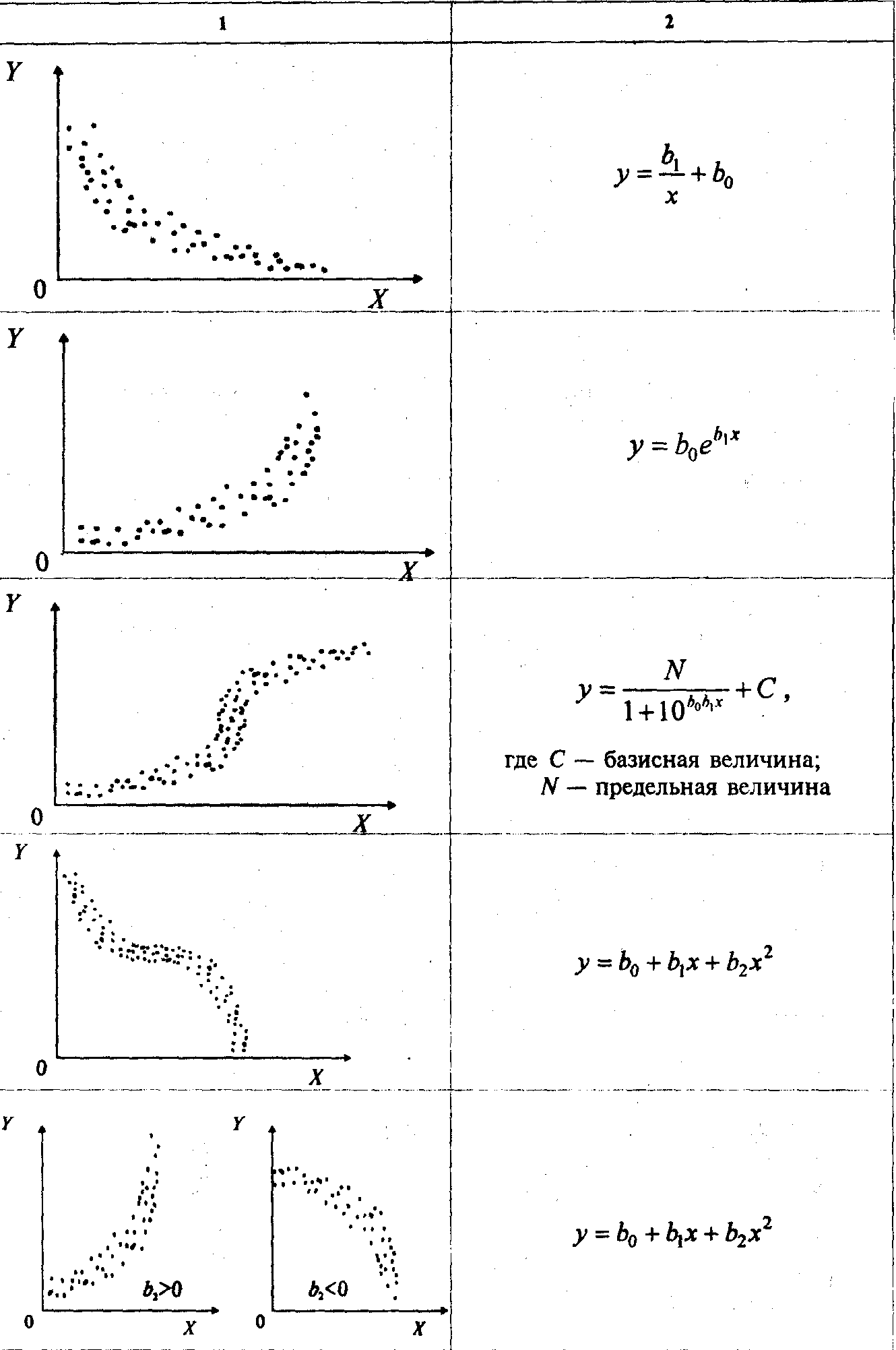
Окончание табл. 6.1.
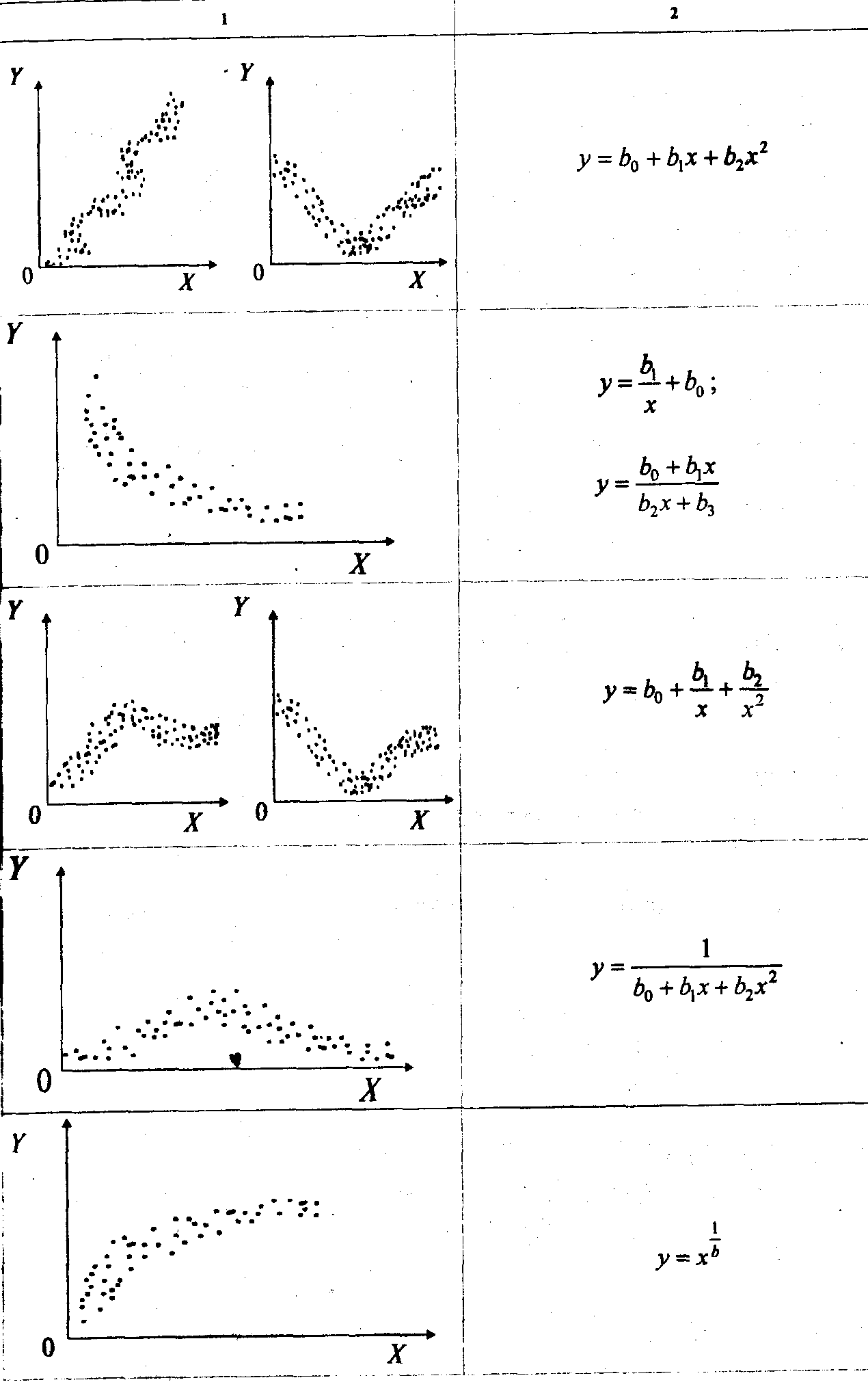
Для полученного уравнения, используя МНК, определяем коэффициенты b0, b1 и b2. Для одного и того же статистического материала могут быть использованы различные формы связи. Луч- шей моделью следует считать ту, которая дает наименьшее значение остаточной дисперсии.
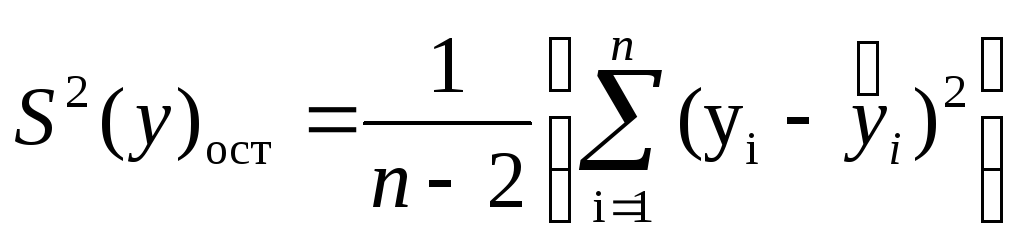
Вычисленные значения коэффициентов уравнения регрессии оценивают при заданном уровне значимости α.
3.4. Динамические статистические модели
При изменении параметров экологического объекта с течением времени широко используются модели, называемые рядами динамики. При изменении целевой функции У от фактора Х, в качестве которого рассматривается время или другой фактор, не зависящий от У, ряды динамики позволяют наглядно представить процесс в виде графиков или таблиц.
По времени, отражаемому в динамических рядах, они разделяются на моментные и интервальные. В моментных рядах уровни ряда выражают величину У на определенную дату, например динамика числа заповедников (табл. 6.2) на конец года.
Таблица 6. 2
|
Годы |
1990 |
1991 |
1992 |
1993 |
1994 |
|
Число заповедников |
72 |
76 |
79 |
85 |
90 |
Уровни моментных рядов динамики суммировать не имеет смысла, поскольку суммирование будет включать одну и ту же величин несколько раз, но разность уровней имеет определенный смысл.
В интервальных рядах уровни ряда выражают размеры явления за определенный промежуток времени. Отличительной особенностью интервальных рядов абсолютных величин является возможность суммировать уровни следующих друг за другом по периодам, поскольку их можно рассматривать как итог за длительный период времени, например лесовосстановление (табл. 6.3).
Таблица 6.3
Посадка леса
|
Годы |
1990 |
1991 |
1992 |
1993 |
1994 |
|
Посадка, га |
566 |
521 |
447 |
428 |
391 |
По полноте времени, отражаемого в рядах динамики, их можно разделить на ряды полные и неполные. В полных рядах даты или периоды следуют друг за другом с равным интервалом, в неполных — в последовательности времени равный интервал не соблюдается.
Большинство статистических характеристик основано на абсолютном или относительном сравнении уровней динамических рядов показателей динамики: абсолютный прирост показателя, темпы рос- та и прироста. Сравниваемый уровень называют текущим, а уро- вень, с которым производится сравнение — базисным. За базисный уровень часто принимается либо предыдущий уровень, либо начальный в данном динамическом ряду.
Если производится сравнение каждого уровня с предыдущим, то получаются цепные показатели динамики. Если каждый уровень сравнивается с начальным или каким-либо одним, принятым за базу сравнения, то получаются базисные показатели.
Абсолютным приростом называется разность последующего и предыдущего уровней ряда динамики
![]()
где уi. — текущий уровень ряда динамики;
уi-1 — предыдущий уровень.
За весь период, описываемый рядом, абсолютный прирост будет равен:
![]()
где уn— последний уровень ряда;
у1 — первый уровень.
Темпом роста называется отношение последующего уровня к предыдущему или к базовому. Темп роста в виде коэффициентов вычисляется по формулам
![]() —
цепные
темпы
роста;
—
цепные
темпы
роста;
![]() —базисные
темпы
роста;
—базисные
темпы
роста;
![]() —темп
роста
за
весь
период.
—темп
роста
за
весь
период.
Темпом прироста называется отношение абсолютного прироста к базисному уровню
![]()
Абсолютное значение одного процента прироста показывает,
какая абсолютная величина скрывается за относительным показателем ― одним процентом прироста. Оно представляет собой отношение абсолютного прироста, выраженному в процентах:
а![]()
следовательно, абсолютное значение одного процента прироста можно вычислить как 0,01 от базисного уровня.
Средним уровнем ряда называется величина
![]()
которая также имеет название хронологической или временной средней.
Такая средняя вычисляется только для интервального ряда. Для моментного ряда средняя вычисляется по формуле
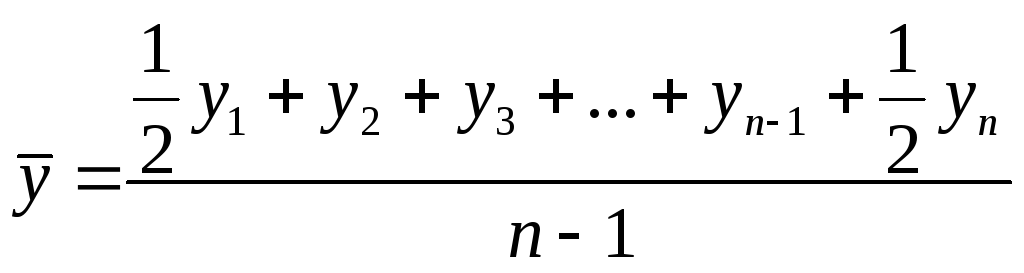
Для моментных рядов динамики при неполных уровнях применяется взвешивание сумм каждой смежной пары уровней по продолжительности периода между ними
![]()
где ti — время между моментом регистрации значений уi и уi+1,
i=1,2,...,п -1.
Средний абсолютный прирост
![]()
При исчислении среднего темпа роста нужно учитывать, что скорость развития явлений идет по правилам сложных процентов, где накапливается прирост на прирост. Поэтому средний темп роста принято вычислять по формуле средней геометрической
![]()
Когда приходится вести расчет средних темпов роста по периодам различной продолжительности, то пользуются средними геометрическими взвешенными по продолжительности периодов
![]()
где ti — интервал времени, в течение которого сохранялся данный темп роста;
![]() —сумма
отрезков
времени
периода.
—сумма
отрезков
времени
периода.
Для выявления основных тенденций развития экологических процессов используются методы выравнивания (сглаживания) рядов. Рассмотрим их.
1. Метод укрупнения интервалов применяется тогда, когда экологические показатели за короткие промежутки времени в силу влияния различных факторов, действующих на них, то повышаются, то понижаются. Из-за этого не видна основная тенденция раз- вития изучаемого явления. Рассматривая приведенные в табл. 6.4 данные по объему сброса сточных вод, мы видим значительные колебания этого показателя, обусловленную главным образом изменением объема производства на данном предприятии.
Таблица 6. 4.