Файл: Математическое моделирование в экологии.doc

(5.4)

Уравнение (5.4) соответствует поступательному движению твердого тела. При вращательном движении используется уравнение:

(5.5)

Второе топологическое уравнение определяет условие непрерывности потоковых переменных. Оно выражает принцип сложения скоростей при сложном движении твердого тела:

геометрическая сумма абсолютной, относительной и переносной скоростей равна нулю.

Поступательное движение:

вращательное движение:

Количество составляемых топологических уравнений вида (5.4), (5.5) равно числу степеней свободы моделируемой системы.

11.5.3. Компонентные и топологические уравнения электрической системы

В электрической системе потоковыми переменными являются токи I (А), а потенциальными переменными – напряжения или потенциалы U (В). Инерционными свойствами обладают катушки индуктивности. Компонентные уравнения инерционного элемента

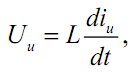
где L – индуктивность (Гн).

Диссипативный элемент – резистор. Его компонентное уравнение получают на основе закона Ома:

U_д = R× i_д,

где R – сопротивление (Ом).

Упругими свойствами характеризуется конденсатор. Компонентное уравнение упругого элемента:

где С - ёмкость (Ф).

Особенностью электрической системы, отличающей её от рассмотренной ранее механической системы, является то, что соединение элементов в электрических схемах образует структуру, в которой легко различаются ветви и узлы. Причем ветви представляют собой двухполюсные элементы – резисторы, конденсаторы, катушки индуктивности, источники энергии и др.

В этом случае топологические уравнения получают на основе законов Кирхгофа:

(5.6)

(5.7)

Уравнение (5.6) выражает первый закон Кирхгофа. Оно записывается для узлов электрической схемы и формулируется так: алгебраическая сумма токов для любого узла электрической схемы равна нулю. Так как ток – потоковая переменная, то первый закон Кирхгофа описывает баланс потоков в узле.

Уравнение (5.7) выражает второй закон Кирхгофа. Оно составляется для замкнутых контуров электрической схемы.

11.5.4. Компонентные и топологические уравнения гидравлической системы

В гидравлической системе потоковыми переменными являются расходы Q (м³/с), а потенциальными переменными – давления p (Н/м² или Па).

Расход жидкости в трубопроводе Q выразим через скорость потока υ

где А – площадь поперечного сечения трубопровода. Введем обозначения:

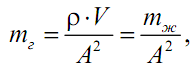
где m_г - коэффициент массы (кг/м⁴); V – объем жидкости в выделенном участке трубопровода длинной l: V=A×l; m_ж – масса жидкости в этом участке.

Компонентным уравнением инерционного элемента является уравнение Эйлера:

Компонентным уравнением диссипативного элемента является уравнение Навье - Стокса:

где µ_г - коэффициент гидравлического сопротивления (Н×с/м⁵).

Упругие свойства жидкости учитывает уравнение Гука:

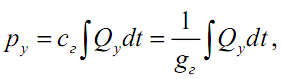
где c_г - коэффициент гидравлической жесткости (Н/м5); g_Г = 1/c_г - коэффициент гидравлической податливости (м⁵/Н); Q_у – изменение расхода, обусловленное сжимаемостью жидкости. В выражении (5.8) учтено, что при возрастании давления происходит увеличение объемной деформации жидкости. Коэффициент c _г определяется по формуле:

где E – модуль объемной упругости жидкости (Н/м²). Переменные p_и, p_у, p_д представляют собой внутренние потенциалы исследуемой гидравлической системы, характеризующие взаимодействие выделенных дискретных элементов и определяющие потери давления источника на преодоление сил инерции жидкости и сообщения ей кинетической энергии, на деформацию жидкости и

изменение её потенциальной энергии, на преодоление сил внутреннего трения жидкости.

Коэффициенты m_г, c_г и µ_г - являются параметрами, соответственно, инерционных, упругих и диссипативных элементов гидравлической системы.

Топологические уравнения имеют вид:

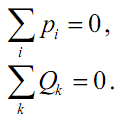
Первое уравнение выражает условие равновесия потенциалов, действующих на сосредоточенные массы, а второе – условие непрерывности потоков жидкости.

11.5.5. Компонентные и топологические уравнения тепловой системы

В тепловой системе (рис.5.1) потенциальной переменной является температура Т (°К), а потоковой переменной – тепловой поток Ф (Вт или Дж/с). Рассмотрим одномерный процесс теплопередачи в твердом теле, полагая, что передача тепловой энергии осуществляется только вдоль оси х. Разделим твердое тело вдоль оси на отрезки длиной l, осуществив тем самым дискретизацию сплошной среды.

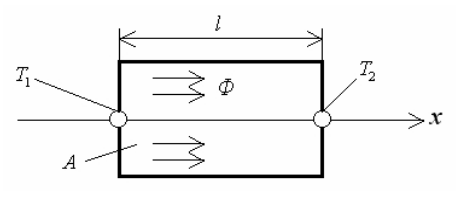
Рис. 5.1. Твёрдое тело

Каждый из полученных при этом дискретных элементов можно характеризовать средними значениями параметров: плотность ρ, теплоемкость с_T, коэффициент теплопроводности λ.

Очевидно, что эти реальные физические элементы, имеющие определенные геометрические формы и объемы, являются сложными, т.к. обладают одновременно упругими и диссипативными свойствами. Однако и в этом случае физические свойства дискретных элементов, так же как в механической или гидравлической системах, можно отобразить простыми абстрактными элементами: упругими и

диссипативными. Изменение тепловой энергии dQ в каждом дискретном элементе

пропорционально приращению его температуры dT. В результате можно записать следующее уравнение теплового баланса:

dQ = C_TdT , (5.8)

где C_T - теплоемкость дискретного элемента (Дж/°К).

Величина теплоемкости определяется по формуле:

C_T = C×ρ×V ,

где С – удельная теплоемкость материала (Дж/кг×°К); V – объем дискретного элемента (м³).

Изменение тепловой энергии в единицу времени представляет собой тепловой поток:

Поэтому уравнение (5.8) перепишем в виде:

Интегрируя последнее уравнение, получаем

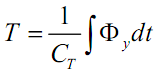
Оно является компонентным уравнением упругого элемента тепловой системы.

Диссипативные свойства тепловой системы описываются уравнением Фурье. В одномерном случае уравнение Фурье имеет вид

(5.9)

где q – плотность теплового потока (Дж/с×м2); λ – коэффициент теплопроводности, Дж/(с×м×^оК).

Плотность теплового потока определяется отношением

где А – площадь поверхности контакта дискретного элемента с источником тепловой энергии или со смежным дискретным элементом, м².

Заменим производную dТ/dх отношением конечной разности

(5.10)

где T₁, T₂- температуры в узлах дискретизации 1 и 2, т.е. на границах выделенных элементов твердого тела; l – длина дискретного элемента. В выражении (5.10) учтено, что градиент температуры вдоль оси х отрицательный (температура падает по мере удаления от источника тепла).

Подставим значение q и dТ/dх в уравнение (5.9):

(5.11)

Формула (5.11) позволяет определить величину падения температуры в дискретном элементе в процессе теплопередачи. Следовательно, она дает математическое описание диссипативного элемента.

Введём обозначение:

(5.12)

где m_T - коэффициент теплового сопротивления дискретного элемента, (Дж/с×°К).

С учетом (5.12) получаем компонентное уравнение диссипативного элемента тепловой системы.

По формуле (5.12) определяют m_T при передаче тепла в твердом теле теплопроводностью, т. е. при индуктивном теплообмене. На поверхностях контакта твердого тела с жидкостной или газовой средой осуществляется конвективный теплообмен. Тепловой поток при конвективном теплообмене, в соответствии с законом Ньютона, пропорционален разности температуры среды T_с и поверхностного

слоя твердого тела T_s.

где T_д = T_c -T_s .

В этом случае коэффициент теплового сопротивления определяется по формуле:

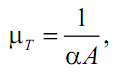
где α - коэффициент теплообмена (теплоотдачи) через конвекцию (Дж/с×м2×°К).

Инерционными свойствами тепловая система не обладает. Это следует из того, что падение температуры вдоль дискретного элемента не зависит от скорости изменения теплового потока, а зависит лишь от его абсолютной величины. Значения потоковой переменной Ф_y характеризует изменение внутренней энергии твердого тела в процессе теплопередачи, а значение Ф_д – величину потерь, обусловленную преодолением теплового сопротивления.