ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 31.03.2024
Просмотров: 1095
Скачиваний: 0
СОДЕРЖАНИЕ
Математическое моделирование элементов сложных экологических систем
Лекция 1. Введение в моделирование. Исторический экскурс.
1. Основы моделирования в экологии 1.1. Общие принципы построения моделей в экологии
2.2. Этапы построения математической модели
1.4. Элементы теории подобия, применяемые в моделировании
3.2.2. Выборочный метод в экологометрике.
Зависимость числа интервалов от объема выборки
Статистический ряд по интервалам
Лекция 4. Статистические оценки параметров распределения случайных величин по выборкам
4.4. Статистические оценки гипотез об экологических моделях
Выборка из генеральной совокупности
Статистическая таблица эксперимента
Пример преобразования членов уравнения регрессии
Вычисление данных для линеаризации уравнения регрессии
Нормальные уравнения мнк для некоторых функций
Статистическое оценивание уравнения регрессии и парной корреляции.
Обработка результатов наблюдений
Рекомендации по выбору вида функции
3.4. Динамические статистические модели
Данные по объему сброса качественных сточных вод
Данные по объему сброса сточных вод за 5-летие
Пример расчета 5-летних средних
Расчетные значения для определения уравнения динамики
Ряд динамики для определения сезонных колебаний
Эксперименталъный материал исследования
8.1. Анализ влияния отдельных факторов в экологической модели.
Лекция 9. Методы оптимизации. Метод Лагранжа
Лекция 10. Метод линейного программирования.
Лекция 11. Функциональные модели.
Лекция 12. Модели процессов содержащие обыкновенные дифференциальные уравнения.
Численные ошибки использованных для вычисления данных
Лекция 13. Статистические модели динамики.
Лекция 16. Информационные технологии в экологии. Экологические информационные системы.
1 6.1. Экологические информационные системы
1. Какова область значения для числовых характеристик?
Лекция 17. Использование информационных технологий для решения задач экологии.
Критические значения коэффициента корреляции rk;α
2.1. Подобие физических явлений и его признаки
2.4. Применение методов подобия в математическом
11.3. Численные методы решения дифференциальных уравнений
11.3.2. Процесс численного решения
11.3.4. Модифицированный метод Эйлера
11.3.6. Метод Рунге – Кутта для систем дифференциальных уравнений
11.3.7. Общая характеристика одношаговых методов
11.3.9. Методы прогноза и коррекции
11.3.10. Краткая характеристика методов прогноза и коррекции.
11.3.11. Выбор шага и погрешность решения.
11.4. Имитационное моделирование систем
11.4.1. Принципы имитационного моделирования
11.4.3. Динамическая модель исследуемого объекта
11.4.4. Построение имитационных моделей динамических систем
11.4.5. Преобразование передаточных функций звеньев в дифференциальные уравнения в форме Коши
11.4.6. Синтез имитационной модели на основе структурной схемы
11.5. Теоретические основы построения математических моделей систем
11.5.1. Компонентные и топологические уравнения
11.5.2. Компонентные и топологические уравнения механической системы
11.5.3. Компонентные и топологические уравнения электрической системы
11.5.4. Компонентные и топологические уравнения гидравлической системы
11.5.5. Компонентные и топологические уравнения тепловой системы
11.6.1. Сущность метода электроаналогий.
11.6.2. Электромеханические аналогии
11.6.3. Построение имитационных моделей методом электроаналогий
11.6.4. Плоское прямолинейное движение звеньев
11.6.5. Электрогидравлические аналогии
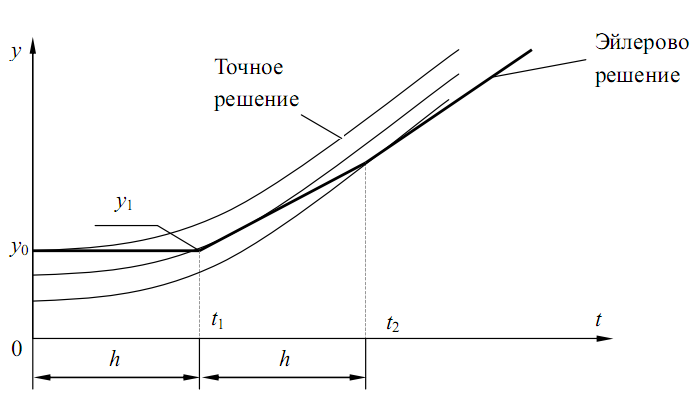
Рис. 3.3 Геометрическая интерпретация метода Эйлера
Практическим следствием этого факта является ожидание того, что при уме-ньшении h приближенное решение будет все более точным и при стремлении h к нулю будет сходиться к точному решению с линейной скоростью по h ; т.е. мы ожидаем, что при уменьшении шага h вдвое ошибка уменьшится в 2 раза. Очень медленная сходимость при уменьшении h характерна для методов первого порядка и служит препятствием для их широкого использования.
Примеры
Определить решение дифференциальных уравнений методом Эйлера.
1) y' = xy .
Решение:
![]()
2)
![]()
Решение:
![]()
3)
![]() .
.
Решение:
![]()
11.3.4. Модифицированный метод Эйлера
Хотя тангенс угла наклона касательной к истинной кривой в исходной точке известен и равен 0 y¢(t ) , он изменяется в соответствии с изменением независимой переменной. Поэтому в точке t0 + h наклон касательной уже не таков, каким он был в точке t0. Следовательно, при сохранении начального наклона касательной на всем интервале h в результаты вычислений вносится погрешность. Точность метода Эйлера можно существенно повысить, используя,
например, среднее значение производной в начале и конце интервала.
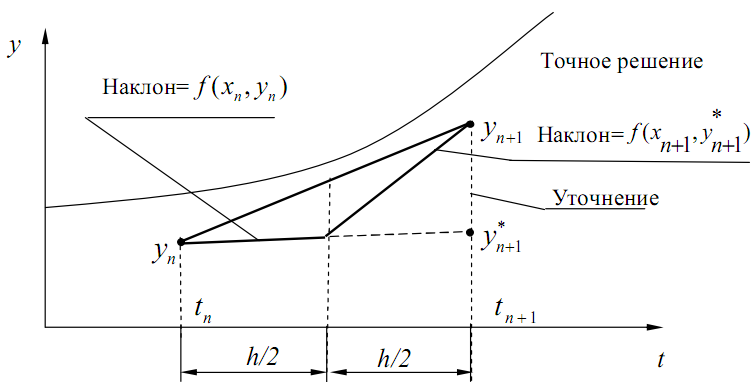
Рис. 3.4. Геометрическая интерпретация модифицированного метода
В модифицированном методе Эйлера сначала вычисляется значение функции в следующей точке по простому методу Эйлера:
![]()
которое используется
для вычисления приближенного значения
производной в конце интервала f(tn+1,
![]() ).
Вычислив среднее между этим значением
призводной и её значением в начале
интервала, найдем более точное значениеyn+1:
).
Вычислив среднее между этим значением
призводной и её значением в начале
интервала, найдем более точное значениеyn+1:
![]() (3.11)
(3.11)
Графическая интерпретация модифицированного метода Эйлера представлена на рис. 3.4. Принцип, на котором основан модифицированный метод Эйлера, можно пояснить иначе. Для этого вернемся к разложению функции в ряд Тейлора.
![]()
Кажется очевидным, что, сохранив член с h2 и отбросив члены более высоких порядков, можно повысить точность. Однако чтобы сохранить член с h2 , надо знать вторую производную y’’(t0) . Её можно аппроксимировать конечной разностью
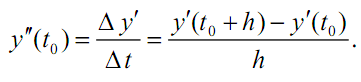
Подставив это выражение в ряд Тейлора с отброшенными членами третьего порядка, найдем
![]()
что совпадает с ранее полученным выражением (3.11).
Этот метод является
методом
второго порядка,
так как в нем используется член ряда
Тейлора, содержащий h2
. За повышение точности приходится
расплачиваться дополнительными
затратами машинного времени, необходимыми
для вычисления
![]() .
.
Примеры:
Определить решение дифференциальных уравнений модифицированным методом Эйлера
1) y’ = xy.
Решение:
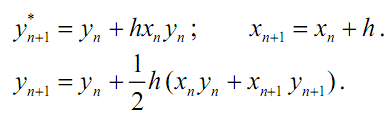
2)
![]()
Решение:
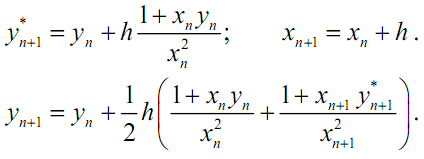
3)
![]()
Решение:
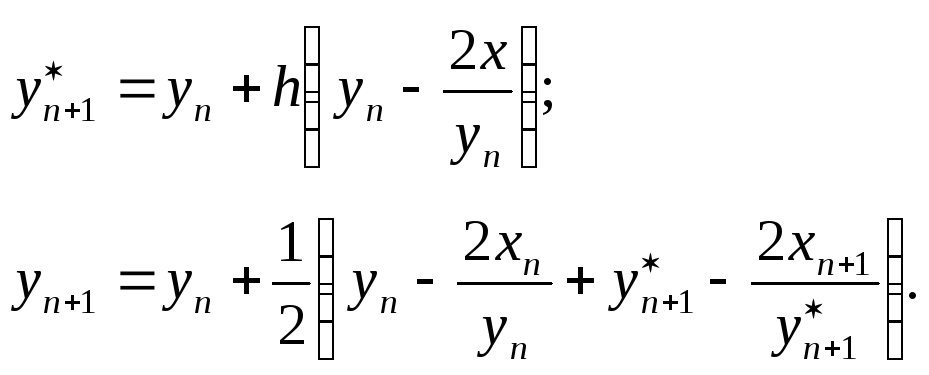
11.3.5. Метод Рунге – Кутта
Пусть требуется найти решение дифференциального уравнения
y’ = f (t, y),
удовлетворяющее начальному условию
y’(t0) = y0.
Принцип, на котором основан метод Рунге – Кутта, можно пояснить, как и принцип, на котором основан метод Эйлера, с помощью разложения функции в ряд Тейлора
![]()
Чтобы удержать в ряде Тейлора член n-го порядка, необходимо вычислить n-ю производную зависимой переменной. При использовании модифицированного метода Эйлера для получения второй производной в конечно-разност-ной форме достаточно было знать наклон кривой на концах рассматриваемого интервала. Чтобы вычислить третью производную в конечно-разностном виде, необходимо иметь значения второй производной, по меньшей мере, в двух точках. Для этого необходимо дополнительно определить наклон кривой в некоторой промежуточной точке интервала h, т. е. между tn и n 1 t + . Очевидно, чем выше порядок вычисляяемой производной, тем больше дополнительных точек потребуется вычислить внутри интервала. Так как существует несколько способов расположения внутренних точек и выбора относительных весов для найденных производных, то метод Рунге – Кутта, в сущности, объединяет целое семейство методов решения дифференциальных уравнений.
Наиболее распространенным из них является метод четвёртого порядка точности, при котором удерживаются все члены ряда Тейлора, включая h4. Расчеты при использовании этого классического метода производятся по формулам:
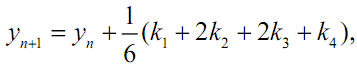
где
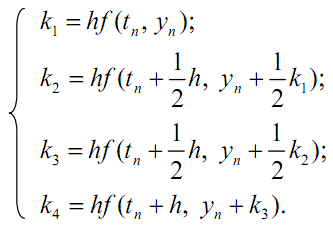
Метод Эйлера и его модификация по сути дела являются методами Рунге – Кутта первого и второго порядка соответственно. Более высокая точность метода Рунге – Кутта позволяет увеличить шаг интегрирования h. Допустимая погрешность на шаге определяет его максимальную величину. В прикладных пакетах программ выбор шага часто осуществляется автоматически. Для этого проводят вычисления сначала с шагом h, а затем – с шагом h/2.
За оценку погрешности вычислений с шагом h/2 можно принять приближенную формулу
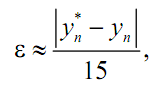
где
![]() - вычисленное значение с шагом h/2;
yn
– вычисленное
значение с шагом h.
Пример: y’
= xy.
- вычисленное значение с шагом h/2;
yn
– вычисленное
значение с шагом h.
Пример: y’
= xy.
Решение:
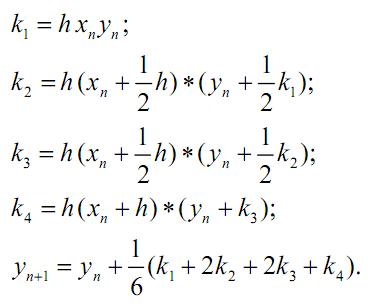
При реализации методов Рунге – Кутта на ЭВМ для каждой точки проводят двойной счет. Если полученные при этом значения удовлетворяют выражению (5.4), то для точки t n+1 шаг удваивают, в противном случае уменьшают вдвое. Однако необходимо помнить, что выражение (5.4) приближенное и при неблагоприятных условиях можно получить совершенно ошибочные результаты, хотя в большинстве случаев дело обстоит благополучно.
11.3.6. Метод Рунге – Кутта для систем дифференциальных уравнений
Формулы Рунге - Кутта можно использовать для решения систем дифференциальных уравнений и, следовательно, для решения дифференциальных уравнений более высоких порядков, так как любое дифференциальное уравнение n-го порядка можно свести к n дифференциальным уравнениям первого порядка. Например, в дифференциальном уравнении второго порядка
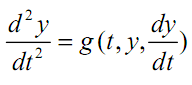
можно принять
![]()
тогда
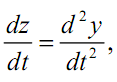
и получаем два уравнения первого порядка:

Задача Коши в этом случае содержит два начальных условия
y(t0) = y0 и z(t0) = z0.
Формулы Рунге – Кутта для рассматриваемого случая имеют
вид:
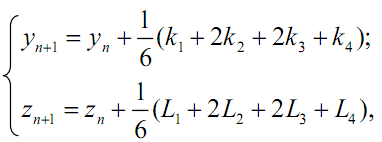
где
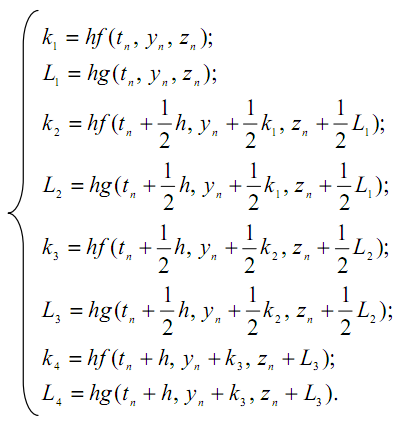
11.3.7. Общая характеристика одношаговых методов
Всем одношаговым методам присущи определенные общие черты:
1) чтобы получить информацию в новой точке, надо иметь данные лишь в одной предыдущей точке. Поэтому одношаговые методы называют «самостартующимися»;
2) в основе всех одношаговых методов лежит разложение функции в ряд Тейлора, в котором сохраняются члены, содержащие h в степени до k включительно. Целое число k называется порядком метода;
3) все одношаговые методы не требуют действительного вычисления производных, а вычисляется лишь сама функция в одной или нескольких промежуточных точках;
4) свойство «самостартования» позволяет легко менять величину шага.
3.8. Многошаговые методы
Вернемся к задаче Коши
y’ = f(t, y); y(0) = y0. (3.13)
В предыдущих методах значение yn + 1 зависело только от информации в пре-дыдущей точке tn. Кажется вполне вероятным, что можно добиться большей точности, если использовать информацию о нескольких предыдущих точках tn, tn - 1,…. Именно так и поступают в многошаговых методах [4].
Если проинтегрировать уравнение (3.13) на отрезке [tn, tn+1], то получим
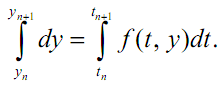
или
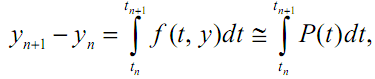
где P(t) – полином, аппроксимирующий f(t, y).
Чтобы построить полином степени N, используем предыдущие решения yn, yn – 1, …. в точках tn,…, tn-1, …, tn - N, ... . Мы по-прежнему считаем, что узлы t расположены равномерно с шагом h. В принципе, можно проинтегрировать этот полином явно, что ведет к следующему методу:
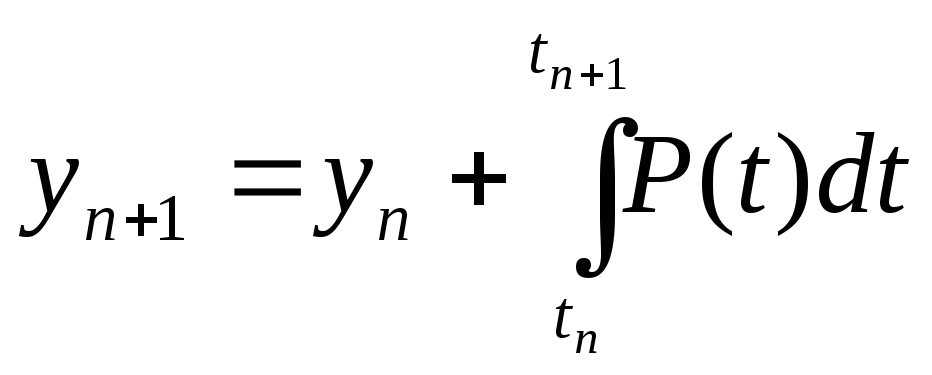 (3.14)
(3.14)
В простейшем случае, когда N = 0, полином P – есть константа, равная fn, и (3.14) превращается в обычный метод Эйлера.
Если N = 1, то P – есть линейная функция, проходящая через
точки (tn-1, fn -1) и (tn, fn) , т. е.