ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 31.03.2024
Просмотров: 1092
Скачиваний: 0
СОДЕРЖАНИЕ
Математическое моделирование элементов сложных экологических систем
Лекция 1. Введение в моделирование. Исторический экскурс.
1. Основы моделирования в экологии 1.1. Общие принципы построения моделей в экологии
2.2. Этапы построения математической модели
1.4. Элементы теории подобия, применяемые в моделировании
3.2.2. Выборочный метод в экологометрике.
Зависимость числа интервалов от объема выборки
Статистический ряд по интервалам
Лекция 4. Статистические оценки параметров распределения случайных величин по выборкам
4.4. Статистические оценки гипотез об экологических моделях
Выборка из генеральной совокупности
Статистическая таблица эксперимента
Пример преобразования членов уравнения регрессии
Вычисление данных для линеаризации уравнения регрессии
Нормальные уравнения мнк для некоторых функций
Статистическое оценивание уравнения регрессии и парной корреляции.
Обработка результатов наблюдений
Рекомендации по выбору вида функции
3.4. Динамические статистические модели
Данные по объему сброса качественных сточных вод
Данные по объему сброса сточных вод за 5-летие
Пример расчета 5-летних средних
Расчетные значения для определения уравнения динамики
Ряд динамики для определения сезонных колебаний
Эксперименталъный материал исследования
8.1. Анализ влияния отдельных факторов в экологической модели.
Лекция 9. Методы оптимизации. Метод Лагранжа
Лекция 10. Метод линейного программирования.
Лекция 11. Функциональные модели.
Лекция 12. Модели процессов содержащие обыкновенные дифференциальные уравнения.
Численные ошибки использованных для вычисления данных
Лекция 13. Статистические модели динамики.
Лекция 16. Информационные технологии в экологии. Экологические информационные системы.
1 6.1. Экологические информационные системы
1. Какова область значения для числовых характеристик?
Лекция 17. Использование информационных технологий для решения задач экологии.
Критические значения коэффициента корреляции rk;α
2.1. Подобие физических явлений и его признаки
2.4. Применение методов подобия в математическом
11.3. Численные методы решения дифференциальных уравнений
11.3.2. Процесс численного решения
11.3.4. Модифицированный метод Эйлера
11.3.6. Метод Рунге – Кутта для систем дифференциальных уравнений
11.3.7. Общая характеристика одношаговых методов
11.3.9. Методы прогноза и коррекции
11.3.10. Краткая характеристика методов прогноза и коррекции.
11.3.11. Выбор шага и погрешность решения.
11.4. Имитационное моделирование систем
11.4.1. Принципы имитационного моделирования
11.4.3. Динамическая модель исследуемого объекта
11.4.4. Построение имитационных моделей динамических систем
11.4.5. Преобразование передаточных функций звеньев в дифференциальные уравнения в форме Коши
11.4.6. Синтез имитационной модели на основе структурной схемы
11.5. Теоретические основы построения математических моделей систем
11.5.1. Компонентные и топологические уравнения
11.5.2. Компонентные и топологические уравнения механической системы
11.5.3. Компонентные и топологические уравнения электрической системы
11.5.4. Компонентные и топологические уравнения гидравлической системы
11.5.5. Компонентные и топологические уравнения тепловой системы
11.6.1. Сущность метода электроаналогий.
11.6.2. Электромеханические аналогии
11.6.3. Построение имитационных моделей методом электроаналогий
11.6.4. Плоское прямолинейное движение звеньев
11.6.5. Электрогидравлические аналогии
Данные по объему сброса качественных сточных вод
|
Год |
Объем сброса сточных вод объектом, тыс. м3 |
Год |
Объем сброса сточных вод объектом, тыс. м3 |
|
1980 1981 1982 1983 1984 1985 1986 1987 |
125,5 130,8 140,2 107,5 152.1 121,1 171,2 147,9 |
1988 1989 1990 199l 1992 1993 1994 l995 |
169,5 162,4 186,8 181,2 168,2 222,5 195,7 140,1 |
Если укрупнить интервалы времени до пятилетнего, то получим новый ряд динамики (табл. 6.5), показывающий последовательное увеличение качественного сброса сточных вод. Здесь же определяется и среднегодовой сброс завода за пятилетие.
Таблица 6. 5
Данные по объему сброса сточных вод за 5-летие
|
Пятилетие, гг |
Качественный сброс сточных вод предприятием, тыс. м3
|
|
|
общий |
среднегодовой
|
|
|
1981 - 1985 |
651,7 |
130,3 |
|
1986 - 1990 |
837,8 |
167,6 |
|
1991 - 1995 |
907,7 |
181,5 |
2. Метод скользящей средней используется при выявлении основной тенденции развития при укрупненных интервалах времени: вместо каждого уровня данного ряда берутся средние из уровней рядом стоящих лет.
Полученная средняя охватывает группу из некоторого числа уровней: трех, пяти, семи и т.д., в середине которой находится взятый. Вместо каждого такого уровня берется средняя, в которой сглаживаются случайные отклонения. Эта средняя будет скользящей, поскольку период осреднения все время меняется: из него вычитается один член и прибавляется следующий. Увеличим период наблюдения еще на 10 лет (табл. 6.6).
Пример. Произвести расчет скользящей средней для статистики по качественному сбросу сточных вод предприятием.
Решение. Производим расчет 5-летних средних и заполняем табл. 6.6. Скользящая средняя дает более или менее плавное изменение уровней. Проводим центрирование, заключающееся в нахождении средней из средних для отнесения полученного уровня к определенной дате.
3. Наиболее эффективным способом выявления основной тенденции --развития является аналитическое выравнивание (определение тренда). При этом уровни ряда динамики выражаются в виде функции времени. Аналитическое выравнивание является предпосылкой для применения других приемов углубленного изучения развития экологических процессов во времени, изучения колеблемости данных в динамике, их связи с другими явлениями.
Таблица 6.6
Пример расчета 5-летних средних
|
Год |
Сброс, тыс. мз |
5-летняя скользящая |
Год |
Сброс, тыс. мз |
5-летняя скользящая |
||
|
сумма |
средняя |
|
|
||||
|
1 |
2 |
3 |
4 |
1 |
2 |
3 |
4 |
|
1970 |
81,2 |
- |
- |
1983 |
107,5 |
623,5 |
130,3 |
|
1971 |
78,7 |
- |
- |
1984 |
152,1 |
656,1 |
138,4 |
|
1972 |
92,2 |
- |
- |
1985 |
121,1 |
651,7 |
139,9 |
|
1973 |
82,5 |
- |
- |
1986 |
171,2 |
692,1 |
152,4 |
|
1974 |
85,6 |
420,4 |
97,8 |
1987 |
147,9 |
699,8 |
154,4 |
|
1975 |
103,7 |
442,7 |
99,9 |
1988 |
169,5 |
761,8 |
167,6 |
|
1976 |
125,0 |
489,0 |
110,3 |
1989 |
162,4 |
772,1 |
169,6 |
|
1977 |
102,6 |
499,4 |
117,1 |
1990 |
186,8 |
837,8 |
173,6 |
|
1978 |
134,7 |
551,6 |
121,5 |
1991 |
181,2 |
847,8 |
184,2 |
|
1979 |
119,5 |
585,5 |
122,6 |
1992 |
168,2 |
868,1 |
189,2 |
|
1980 |
125,5 |
607,3 |
130,1 |
1993 |
222,5 |
921,1 |
181,5 |
|
1981 |
130,8 |
613,1 |
124,7 |
1994 |
195,7 |
947,4 |
- |
|
1982 |
140,2 |
650,7 |
131,2 |
1995 |
140,1 |
907,7 |
- |
Аналитическое выравнивание состоит в подборе для данного ряда динамики теоретической кривой выражающей основные черты фактической динамики. Здесь часто применяют МНК. Рассмотрим технику аналитического выравнивания ряда динамики по прямой
![]() .
.
По МНК имеем систему нормальных уравнений
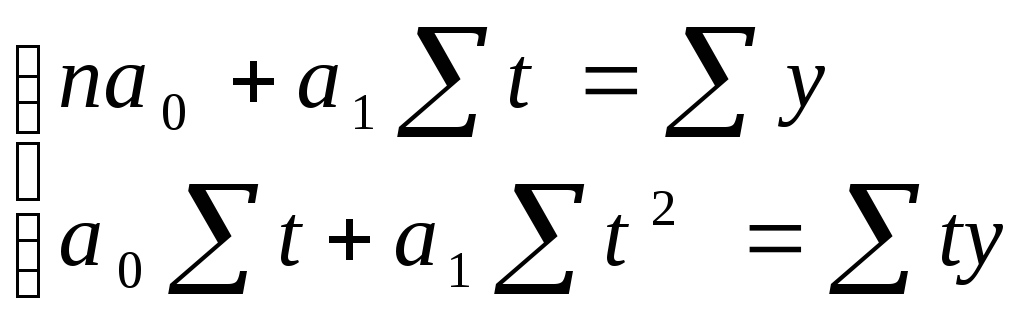
где n — число членов ряда динамики.
Система уравнений упрощается, если t подобрать так, чтобы их сумма равнялась нулю, т.е. начало отсчета времени перенести в сере- дину рассматриваемого периода. Тогда
![]() ,
,
![]() .
.
Если число уровней четное, то условное обозначение времени принимает вид, как показано в табл. 6.7.
Таблица 6.7
Условное обозначение времени
|
Год |
1989 |
1990 |
1991 |
1992 |
1993 |
1994 |
1995 |
1996 |
|
Уровень |
-7 |
-5 |
-3 |
-1 |
+1 |
+3 |
+5 |
+7 |
При
нечетном
числе
членов ряда
отсчет
ведется
от
середины,
взятой
за ноль. Значение
![]() при четном числе уровней
при четном числе уровней
![]()
при нечетном
![]()
Пример. По данным таблицы 6.7 найти уравнение динамики у=ао+а1t.
Р е
ш
е
н
и
е.
Вычисляем
параметры
![]() ,
,
![]() ,
уi.
и
заносим
в
табл.
6.8.
,
уi.
и
заносим
в
табл.
6.8.
Таблица 6.8
Расчетные значения для определения уравнения динамики
|
Год |
Процент загрязнения воздуха от уровня ПДК (Y) |
ti |
ti2 |
уiti |
Теоретические значения уi |
|
1 |
2 |
3 |
4 |
5 |
6 |
|
1987 |
39,4 |
-9 |
81 |
-354,6 |
39,29 |
|
1988 |
39,8 |
-7 |
49 |
-278,6 |
39,73 |
|
1989 |
40,0 |
-5 |
25 |
-200,0 |
40,17 |
|
1990 |
40,6 |
-3 |
9 |
-121,8 |
40,61 |
|
1991 |
41,4 |
-1 |
1 |
-41,4 |
41,05 |
|
1992 |
41,9 |
+1 |
1 |
41,9 |
41,49 |
|
1993 |
41,9 |
+3 |
9 |
125,7 |
41,93 |
|
1994 |
42,0 |
+5 |
25 |
213,0 |
42,37 |
|
1995 |
42,6 |
+7 |
49 |
300,2 |
42,81 |
|
1996 |
43,1 |
+9 |
81 |
387,9 |
43,25 |
|
Сумма |
412,7 |
0 |
330 |
72,3 |
412,70 |
Из таблицы находим: при n = 10
![]()
![]()
тогда уравнение прямой будет иметь вид
![]() .
.
По полученному уравнению находим теоретические значения процента загрязнения воздуха от уровня ПДК для каждого периода времени.
Мерой колеблемости уровней динамического ряда выступает средний квадрат отклонений фактических уровней ряда от переменных уровней, исчисляемых по тренду. Эта величина подобна дисперсии, исчисляемой в рядах распределения с той разницей, что отсчет отклонений ведется не от средней (постоянной для данного ряда), а от переменной средней — выровненных уровней. Мера колеблемости определяется по формуле
![]()
Для тренда (см. табл. 6.7), выраженного прямой уi = 41,27 + 0,22t, мера колеблемости будет равна:
![]() =1/10
-[(39,4
-
39,29)2+(39,8
-
39,73)2+(40,0
-
40,17)2+
(40,6
-
40,61)2+(41,4-
41,05)2+(41,9
-
41,49)2+(41,9-
41,93)2+(42,0
-
42,37)2+(42,6
-
42,81)2+(43,1-
43,25)2]
=
0,055
=1/10
-[(39,4
-
39,29)2+(39,8
-
39,73)2+(40,0
-
40,17)2+
(40,6
-
40,61)2+(41,4-
41,05)2+(41,9
-
41,49)2+(41,9-
41,93)2+(42,0
-
42,37)2+(42,6
-
42,81)2+(43,1-
43,25)2]
=
0,055
Относительная мера колеблемости (своеобразный коэффициент вариации) определяется по формулам:
![]() ;
;
![]()
для нашего примера
![]()
![]()
а в процентах Vt%=Vt • 100 = 0,0057•100 = 0,57%. Величина Vt служит критерием правильности выбора уравнения тренда.
Сезонные колебания параметров экологических процессов. Многие экологические процессы изменяют свой характер в зависимости от смены сезонов года. Такие изменения вызывают сезонные колебания тех или иных параметров этих процессов. Изучение сезонных колебаний имеет самостоятельное значение как исследование особого типа динамики.