ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 31.03.2024
Просмотров: 1055
Скачиваний: 0
СОДЕРЖАНИЕ
Математическое моделирование элементов сложных экологических систем
Лекция 1. Введение в моделирование. Исторический экскурс.
1. Основы моделирования в экологии 1.1. Общие принципы построения моделей в экологии
2.2. Этапы построения математической модели
1.4. Элементы теории подобия, применяемые в моделировании
3.2.2. Выборочный метод в экологометрике.
Зависимость числа интервалов от объема выборки
Статистический ряд по интервалам
Лекция 4. Статистические оценки параметров распределения случайных величин по выборкам
4.4. Статистические оценки гипотез об экологических моделях
Выборка из генеральной совокупности
Статистическая таблица эксперимента
Пример преобразования членов уравнения регрессии
Вычисление данных для линеаризации уравнения регрессии
Нормальные уравнения мнк для некоторых функций
Статистическое оценивание уравнения регрессии и парной корреляции.
Обработка результатов наблюдений
Рекомендации по выбору вида функции
3.4. Динамические статистические модели
Данные по объему сброса качественных сточных вод
Данные по объему сброса сточных вод за 5-летие
Пример расчета 5-летних средних
Расчетные значения для определения уравнения динамики
Ряд динамики для определения сезонных колебаний
Эксперименталъный материал исследования
8.1. Анализ влияния отдельных факторов в экологической модели.
Лекция 9. Методы оптимизации. Метод Лагранжа
Лекция 10. Метод линейного программирования.
Лекция 11. Функциональные модели.
Лекция 12. Модели процессов содержащие обыкновенные дифференциальные уравнения.
Численные ошибки использованных для вычисления данных
Лекция 13. Статистические модели динамики.
Лекция 16. Информационные технологии в экологии. Экологические информационные системы.
1 6.1. Экологические информационные системы
1. Какова область значения для числовых характеристик?
Лекция 17. Использование информационных технологий для решения задач экологии.
Критические значения коэффициента корреляции rk;α
2.1. Подобие физических явлений и его признаки
2.4. Применение методов подобия в математическом
11.3. Численные методы решения дифференциальных уравнений
11.3.2. Процесс численного решения
11.3.4. Модифицированный метод Эйлера
11.3.6. Метод Рунге – Кутта для систем дифференциальных уравнений
11.3.7. Общая характеристика одношаговых методов
11.3.9. Методы прогноза и коррекции
11.3.10. Краткая характеристика методов прогноза и коррекции.
11.3.11. Выбор шага и погрешность решения.
11.4. Имитационное моделирование систем
11.4.1. Принципы имитационного моделирования
11.4.3. Динамическая модель исследуемого объекта
11.4.4. Построение имитационных моделей динамических систем
11.4.5. Преобразование передаточных функций звеньев в дифференциальные уравнения в форме Коши
11.4.6. Синтез имитационной модели на основе структурной схемы
11.5. Теоретические основы построения математических моделей систем
11.5.1. Компонентные и топологические уравнения
11.5.2. Компонентные и топологические уравнения механической системы
11.5.3. Компонентные и топологические уравнения электрической системы
11.5.4. Компонентные и топологические уравнения гидравлической системы
11.5.5. Компонентные и топологические уравнения тепловой системы
11.6.1. Сущность метода электроаналогий.
11.6.2. Электромеханические аналогии
11.6.3. Построение имитационных моделей методом электроаналогий
11.6.4. Плоское прямолинейное движение звеньев
11.6.5. Электрогидравлические аналогии
где τ — переменная интегрирования;
α — коэффициент;
у — зависимая переменная, которая называется состоянием системы;
t — независимая переменная, которая может быть не только временем;
у0 — не зависящее от времени начальное условие;
x(τ) — детерминированная входная функция (возмущающая сила).
Для того чтобы получить наблюдаемую зависимую переменную Y(t), к функции у(τ) следует добавить ненаблюдаемую ошибку ε(t). Для дискретных наблюдений
Y(ti) = y(ti)+ ε(ti),
а для непрерывных переменных
Y(i) = y(t)+ ε(t)
Если
параметр,
α
заменить
его
оценкой
![]() ,
то
остаточная
ошибка
определяется
,
то
остаточная
ошибка
определяется
Е(t)
=
Y(t)
-
![]() (t).
(t).
Целью оценивания параметров является получение значения параметра, а в процессе наблюдений Y(ti) и Y(t). Чтобы сделать это, необходимо знать функцию х(t) и иметь некоторую информацию о характере ε(t).
Более общей является модель, содержащая систему линейных обыкновенных дифференциальных уравнений первого порядка с постоянными коэффициентами (рис. 12.6)
![]() .
.
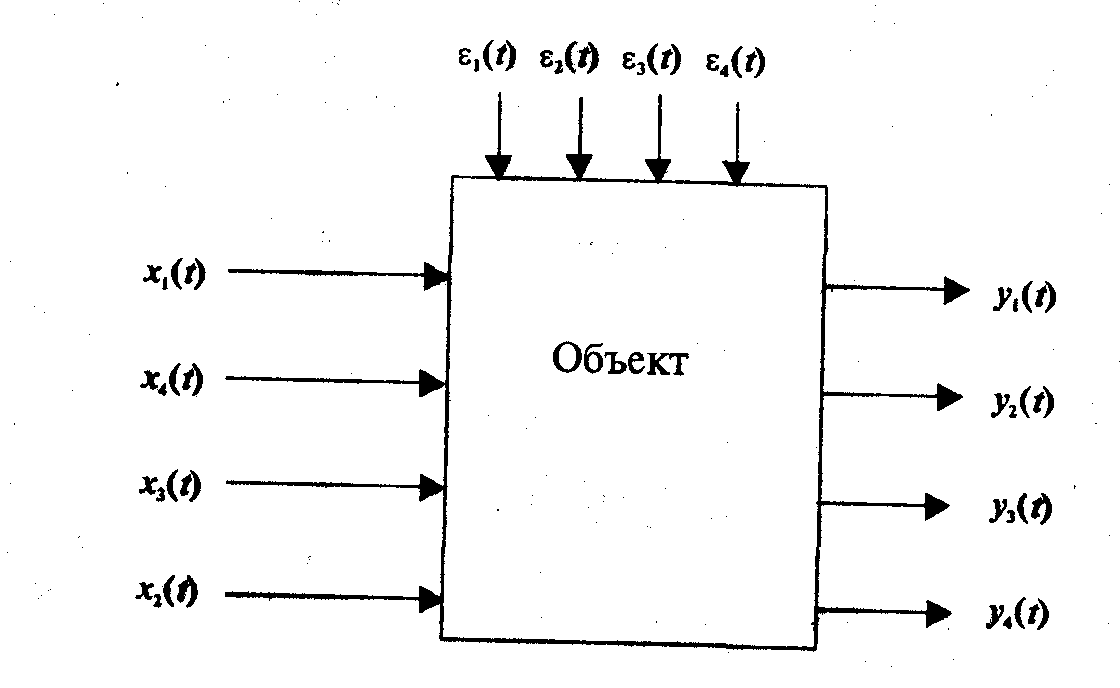
Рис. 12.6. Многомерный процесс с несколькими входами
В матричной форме модель имеет вид:
![]() ,
,
![]() .
.
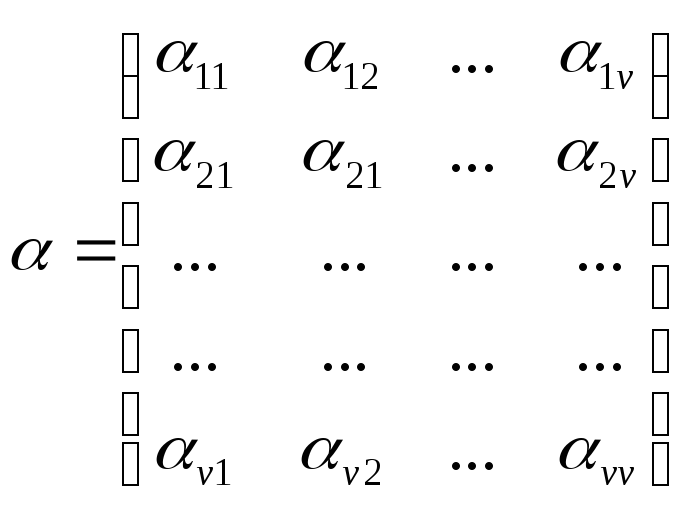 ;
Y=
;
Y=
![]() ;
Х=
;
Х=
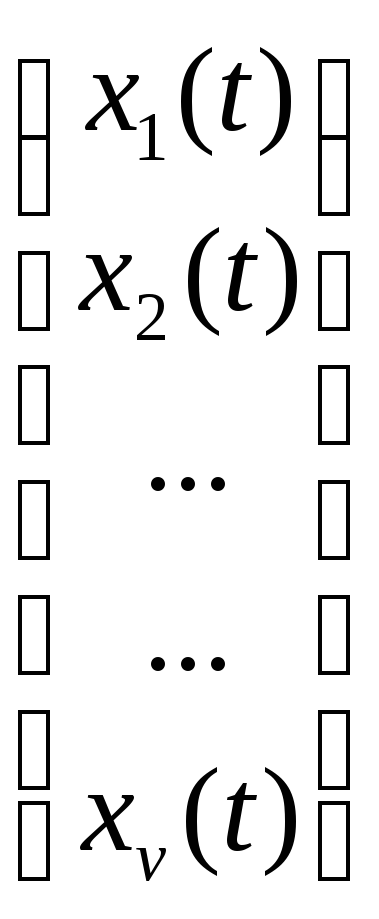 .
.
Тогда решение можно записать в форме
![]() .
.
Модель, содержащую одно или несколько линейных дифференциальных уравнений более высокого порядка с постоянными коэффициентами, например
![]() ,
,
можно преобразовать в модель, содержащую систему обыкновенных дифференциальных уравнений первого порядка, следующим образом. Введём обозначения
![]()
![]()
Тогда уравнение второго порядка будет представлено в виде двух уравнений первого порядка
![]() ,
,
![]() ,
,
однако функция, а в действительности является производной.
Общая нелинейная модель первого порядка имеет вид
![]() ,
,
![]()
где F(α,Y,t) представляет собой весьма общую нелинейную функцию. Уравнение, за редким исключением, не имеет аналитического решения и его следует решать численными методами.
Вследствие трудностей получения аналитических решений для детерминированной модели процесса
![]()
эксперименты должны быть поставлены так, чтобы измерялся вектор производных dy/dt а не сам вектор Y. Если наблюдаемой переменной является производная, то процедура оценивания вообще не затрагивает дифференциального уравнения; параметры и начальные условия можно оценить методами регрессионного анализа.
Другой способ (менее удовлетворительный) позволяет избежать операций с производными при оценивании. Он состоит в использовании численных значений производных, полученных по наблюдениям величины Y.
Вычисленные производные содержат два основных вида ошибок: вводимые при использовании численной схемы и случайные ошибки, связанные с наблюдениями.
Исследуем численную оценку. Численное дифференцирование детерминирова-нных переменных предусматривает вычисление dy/dt или высших производных при некотором произвольном значении независимой переменной t (напри-мер, t0) по заданному ряду значений у в некотором интервале вблизи t0. Детерминированная ошибка в производной становится меньше, если данные концентрируются около значения t0, расположенного в середине интервала изменения t, чем когда значение t0 попадает на тот или другой конец интервала. Вместо непрерывной производной можно использовать любой из интерполяционных многочленов (Лагранжа, Грама).
Большинство схем аппроксимации для производных можно записать в общей форме
![]() )
)
где аi— постоянные;
D — дифференциальный оператор;
k — порядок производной;
h — фиксированное приращение независимой переменной;
(m+1) — число используемых опорных точек.
Следовательно, дисперсию производной можно оценить с по- мощью формулы переноса ошибок, предполагая, что величины Y, стохастически не зависимы, (но это практически маловероятно)
![]() .
.
Если принять дисперсии всех величин уi, равными друг другу, то
![]() .
.
Отсюда видно, что чем меньше интервал h и чем больше членов в формуле, тем больше ошибка в производной. Эта ошибка растет с увеличением порядка производной.
Пример. В табл. 12.4 представлены численные ошибки для не- скольких разностных формул, использованных для вычисления температурного градиента в стенке (dТ/dz)z0 по измеренным значениям температуры, которая считалась детерминированной переменной.
Таблица 12.4
Численные ошибки использованных для вычисления данных
|
Степень много- члена |
Аппроксимация dT/dz при z =2 |
Порядок остаточного члена |
Численное значение (dT/dz)z0= 0 |
|
1 |
(Т1 — Т0) / h |
h |
4,12 |
|
2 |
(-Т2 + 4Т1 — 3Т0) / 2h |
h2 |
4,71 |
|
3 |
(-2Т3 - 9T2 + 18Т1 - 11T0)/ 6h |
h3 |
5,25 |
|
4 |
(-3T4+ 16Т3 - 36Т2+ 48Т1 - 25T0)/12h |
h4 |
3,47 |
Здесь аппроксимация градиента d/Т/dz и «порядок ошибки» маскируют значительно более важный источник ошибки при вычислении dT/dz, а именно случайную ошибку, порождаемую измерением.
Предположим, что все величины Тi в табл. 12.4 обладают одинаковым стандартным отклонением 0,01 (1% от Т0) или дисперсией в 10-4. Тогда для многочлена четвертого порядка
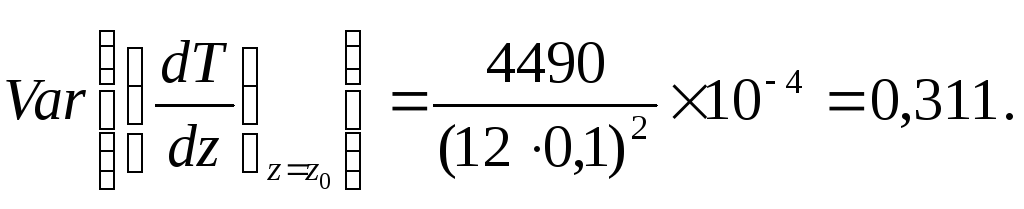
при
измерениях:
To
=-1,000;
Т1=-0,588;
Т2=-0,295;
Т3=-0,259;
T4=-0,305;
h
= 0,1.
Тогда
![]() ,
что
составляет
около
16%
от
,
что
составляет
около
16%
от
![]() .
.
Оценивание методом наименьших квадратов. Если наблюдения Y для откликов модели представляют собой непрерывные функции времени в интервале от t = 0 до t = ti то МНК требует минимизировать величину
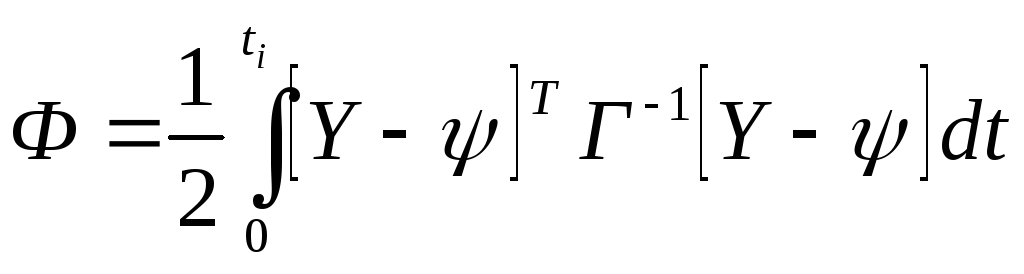 ,
,
где Г — ковариационная матрица;
Ф — проинтегрированное по времени значение квадрата ошибки. Если наблюдения производились в дискретные моменты времени ti, i= 1, 2, ..., n, то, согласно критерию Маркова, следует минимизировать величину
![]() .
.
Если
матрица
Г
является
диагональной,
то
Ф
соответствует
критерию
«взвешенных наименьших
квадратов».
Если
же
Г
=
![]() получается
критерий
«обыкновенных наименьших
квадратов».
получается
критерий
«обыкновенных наименьших
квадратов».
Величина ψ в общей форме
ψ (α,у0,ti) = Y(ti) - ε(ti),
ε(ti) = Y(ti) - ψ (ti).
т.е.
Для минимизации дифференцируем функцию Ф по у0 и α.
Приравниваем ее нулю
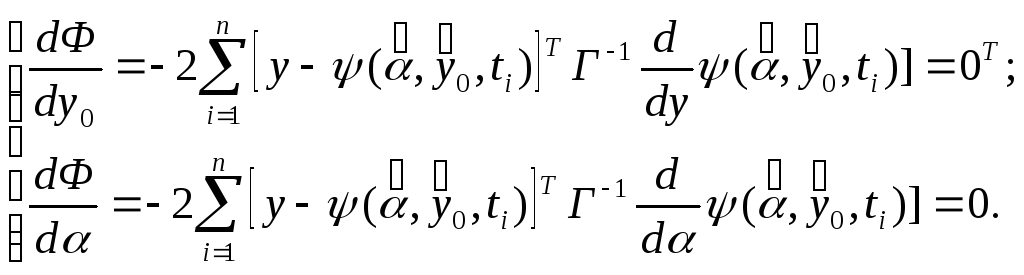
Подобную
систему
уравнений
можно
получить
и
для
непрерывных
данных, заменяя
суммы
по
дисперсионным
значениям
на
интегралы
по
времени.
Для получения
оценки
точности
![]() и
и
![]() необходимо
сделать
некоторое
предположение относительно
распределения
ненаблюдаемых
ошибок,
например,
постулировать
нормальное
совместное
распределение.
необходимо
сделать
некоторое
предположение относительно
распределения
ненаблюдаемых
ошибок,
например,
постулировать
нормальное
совместное
распределение.
Чтобы
получить
оценки
точности
![]() ,
решение
модели
необходимо
приближенно
представить в
виде
линейной
функции
параметров,
разлагая
это
решение
в
ряд
относительно оценок
этих
параметров
линеаризацией.
,
решение
модели
необходимо
приближенно
представить в
виде
линейной
функции
параметров,
разлагая
это
решение
в
ряд
относительно оценок
этих
параметров
линеаризацией.
Пример. Пусть имеем модель
![]()
![]() .
.
Тогда
![]() .
.![]()
Дифференцируя
![]()
по у0 а затем по α и заменяя в получившихся выражениях у0 и α на их оценки получим: