Файл: Математическое моделирование в экологии.doc

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 31.03.2024

Просмотров: 1154

Скачиваний: 0

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

СОДЕРЖАНИЕ

Конспект лекций

Владикавказ

Математическое моделирование элементов сложных экологических систем

Лекция 1. Введение в моделирование. Исторический экскурс.

1. Основы моделирования в экологии 1.1. Общие принципы построения моделей в экологии

Лекция 2.

2.1. Элементы моделирования

2.2. Этапы построения математической модели

1.4. Элементы теории подобия, применяемые в моделировании

Лекция 3

3.2. Экологические модели

3.2.1. Основы экологометрики

3.2.2. Выборочный метод в экологометрике.

Зависимость числа интервалов от объема выборки

Статистический ряд по интервалам

Лекция 4. Статистические оценки параметров распределения случайных величин по выборкам

4.4. Статистические оценки гипотез об экологических моделях

Определение вариантов выборок

Выборка из генеральной совокупности

Статистическая таблица

Лекция 5.

Результаты эксперимента

Статистическая таблица эксперимента

Пример преобразования членов уравнения регрессии

Вычисление данных для линеаризации уравнения регрессии

Нормальные уравнения мнк для некоторых функций

Статистическое оценивание уравнения регрессии и парной корреляции.

Обработка результатов наблюдений

Лекция 6.

Рекомендации по выбору вида функции

3.4. Динамические статистические модели

Посадка леса

Данные по объему сброса качественных сточных вод

Данные по объему сброса сточных вод за 5-летие

Пример расчета 5-летних средних

Условное обозначение времени

Расчетные значения для определения уравнения динамики

Ряд динамики для определения сезонных колебаний

Лекция 7. Многофакторные эколого-математические модели. Анализ влияния отдельных факторов в экологической модели.

Эксперименталъный материал исследования

Результаты проведенных опытов

8.1. Анализ влияния отдельных факторов в экологической модели.

Лекция 9. Методы оптимизации. Метод Лагранжа

Лекция 10. Метод линейного программирования.

Лекция 11. Функциональные модели.

Лекция 12. Модели процессов содержащие обыкновенные дифференциальные уравнения.

Численные ошибки использованных для вычисления данных

Лекция 13. Статистические модели динамики.

Лекция 14. Балансовые модели.

Лекция 15.

Лекция 16. Информационные технологии в экологии. Экологические информационные системы.

1 6.1. Экологические информационные системы

1. Какова область значения для числовых характеристик?

Лекция 17. Использование информационных технологий для решения задач экологии.

Специальные приложения.

Значение функции

Значение критерия

Значение критерия

Критические значения коэффициента корреляции rk;α

2. Основы теории подобия

2.1. Подобие физических явлений и его признаки

2.2. Анализ размерностей

2.3. Первая теорема подобия

2.4. Применение методов подобия в математическом

11.3. Численные методы решения дифференциальных уравнений

11.3.1. Постановка задачи

11.3.2. Процесс численного решения

11.3.3. Метод Эйлера

11.3.4. Модифицированный метод Эйлера

11.3.5. Метод Рунге – Кутта

11.3.6. Метод Рунге – Кутта для систем дифференциальных уравнений

11.3.7. Общая характеристика одношаговых методов

3.8. Многошаговые методы

11.3.9. Методы прогноза и коррекции

11.3.10. Краткая характеристика методов прогноза и коррекции.

11.3.11. Выбор шага и погрешность решения.

11.3.12. Жесткие задачи

11.4. Имитационное моделирование систем

11.4.1. Принципы имитационного моделирования

11.4.2. Объекты моделирования

11.4.3. Динамическая модель исследуемого объекта

11.4.4. Построение имитационных моделей динамических систем

11.4.5. Преобразование передаточных функций звеньев в дифференциальные уравнения в форме Коши

11.4.6. Синтез имитационной модели на основе структурной схемы

11.5. Теоретические основы построения математических моделей систем

11.5.1. Компонентные и топологические уравнения

11.5.2. Компонентные и топологические уравнения механической системы

11.5.3. Компонентные и топологические уравнения электрической системы

11.5.4. Компонентные и топологические уравнения гидравлической системы

11.5.5. Компонентные и топологические уравнения тепловой системы

11.6. Метод электроаналогий

11.6.1. Сущность метода электроаналогий.

11.6.2. Электромеханические аналогии

11.6.3. Построение имитационных моделей методом электроаналогий

11.6.4. Плоское прямолинейное движение звеньев

11.6.5. Электрогидравлические аналогии

11.6.6. Электротепловые аналогии

Литература

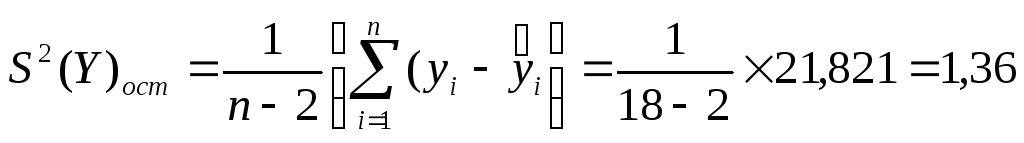
Принимаем уровень значимости, α = 0,1 и при числе степеней свободы k1 = 18 - 1 = 17; k2 = 18 - 2 = 16, по таблице (см. приложение 6) находим значение критерия Фишера

Сравниваем =F17;16;0,1 = 1,94.

Fb =3,13>F17;16;0,1 =1,94 =1,067х,

т.е. уравнение регрессии = 1,067х адекватно описывает результаты эксперимента.

4. Для проверки линейности уравнения регрессии используется следующий подход. Так как изменение функции отклика Y носит случайный характер, то при каждом значении Х рекомендуется проводить по несколько экспериментов, чтобы для данного значения Х получить некоторое среднее значение Y.

В этом случае экспериментальный материал табл. 5.2 представляется в виде табл. 5.6, в которой принимается k уровней Х, а число значений Y для Хi берется равным mi. Общее число экспериментов равно:

Значение Y в j-том эксперименте для Хi обозначаем как Yij, среднее значение для Хi равно:

Для проверки линейности уравнения регрессии вычисляется Fл статистика

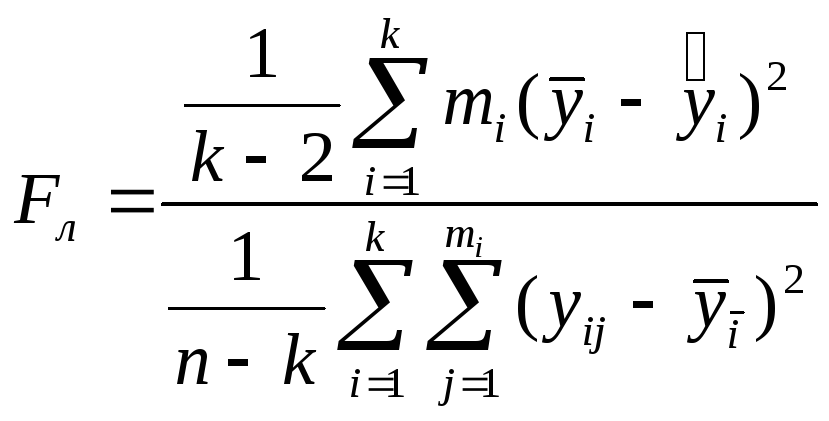
которая сравнивается с критерием Фишера при уровне значимости α и степенях свободы испытаний k1 = n — 1, k2 = n — 2. При Fл< — гипотеза о линейности уравнения регрессии принимается, а при Fл> гипотеза о линейности отвергается.

Во втором случае для описания экспериментального материала необходимо выбрать нелинейную модель (табл. 5.8).

Таблица 5.8

Обработка результатов наблюдений

Уровни значений

Xi

Полученные значения Y при Xi

Число опытов

mi

сред- нее значе- нне

уi

Сумма квадра- тов раз- ности

(при b0=0, b1 =1,07)

Вычисления

1

2

3

1

2

3

4

5

6

7

8

9

10

1

3

2

1

3

2,00

2,00

1,070

0,93

2,611

2

2

3

3

3

2,67

1,11

2,140

0,53

0,861

3

4

3

5

3

4,00

2,00

3,210

0,79

1,915

4

4

5

6

3

5,00

2,00

4,280

0,72

1,607

5

4

6

6

3

5,33

2,67

5,350

0,02

0,07

6

7

8

8

3

7,67

0,33

6,420

1,25

4,823

21

24

27

29

18

26,67

10,11

22,47

4,24

11,82

Пример. По результатам наблюдений, приведенных в табл. 5.1, проверить линейность уравнения регрессии у = 1,07x .

Р е ш е н и е. Результаты наблюдений табл. 5.1 обрабатываем и представляем в виде табл. 5.6. Определяем Fл статистику

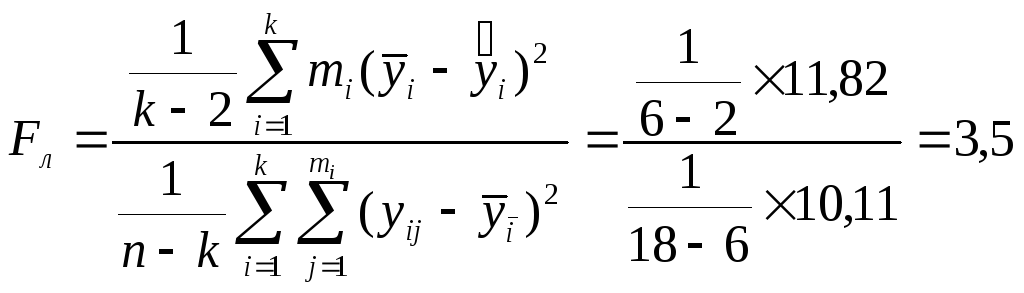
При уровне значимости, а = 0,05 и числе степеней k1 = 6 - 2 = 4; k2 = 18 - 6 = 12 по таблице (см. приложение 6, в) выбираем F4;12;0,05 = 5,91.

Сравниваем Fл = 3,5 < F4;12;0,05 = 5,91.

Следовательно, гипотезу о линейности уравнения регрессии у = 1,07к следует принять.

5. Доверительные интервалы для уравнения регрессии определяются по формуле

где — значение уравнения регрессии для хi, полученное МНК;

—средняя ошибка отдельного значения уi;

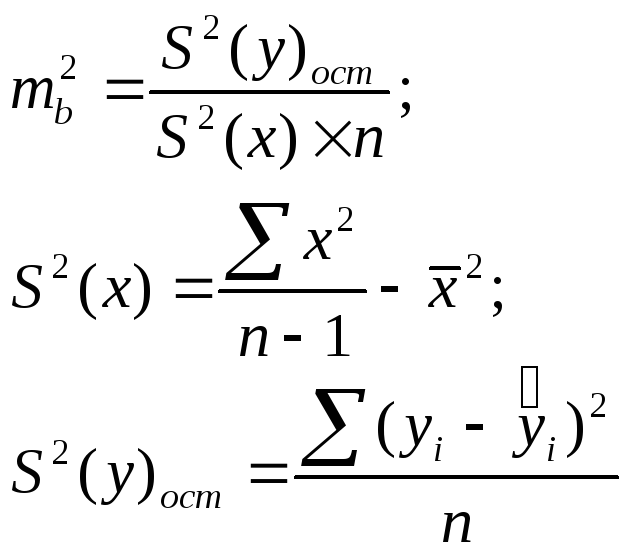
При заданной величине уровня значимости α и числе степеней свободы k = n -1, величина tα;k принимается по таблице (см. приложение 2).

Для нашего примера при хi. = 1, = 1,07:

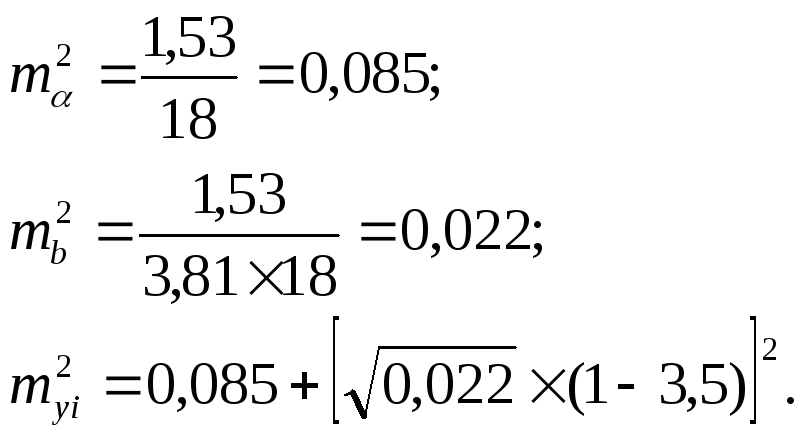
При α = 0,1; k = 18 — 1 = 17; t0,1;17 = 1,740, тогда Отсюда для хi=1 и уi= 1,07:

1,07 - 0,82 1,07+ 0,82;

0,25 1,89.

Величина ошибки = зависит от того, насколько далеко отстоит каждое значение хi от среднего х. Ошибка коэффициента корреляции определяется по формуле

Доверительный интервал имеет вид

Для нашего примера

при t0,1;17=1

назад

Смотрите также файлы