ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 31.03.2024
Просмотров: 1148
Скачиваний: 0
СОДЕРЖАНИЕ
Математическое моделирование элементов сложных экологических систем
Лекция 1. Введение в моделирование. Исторический экскурс.
1. Основы моделирования в экологии 1.1. Общие принципы построения моделей в экологии
2.2. Этапы построения математической модели
1.4. Элементы теории подобия, применяемые в моделировании
3.2.2. Выборочный метод в экологометрике.
Зависимость числа интервалов от объема выборки
Статистический ряд по интервалам
Лекция 4. Статистические оценки параметров распределения случайных величин по выборкам
4.4. Статистические оценки гипотез об экологических моделях
Выборка из генеральной совокупности
Статистическая таблица эксперимента
Пример преобразования членов уравнения регрессии
Вычисление данных для линеаризации уравнения регрессии
Нормальные уравнения мнк для некоторых функций
Статистическое оценивание уравнения регрессии и парной корреляции.
Обработка результатов наблюдений
Рекомендации по выбору вида функции
3.4. Динамические статистические модели
Данные по объему сброса качественных сточных вод
Данные по объему сброса сточных вод за 5-летие
Пример расчета 5-летних средних
Расчетные значения для определения уравнения динамики
Ряд динамики для определения сезонных колебаний
Эксперименталъный материал исследования
8.1. Анализ влияния отдельных факторов в экологической модели.
Лекция 9. Методы оптимизации. Метод Лагранжа
Лекция 10. Метод линейного программирования.
Лекция 11. Функциональные модели.
Лекция 12. Модели процессов содержащие обыкновенные дифференциальные уравнения.
Численные ошибки использованных для вычисления данных
Лекция 13. Статистические модели динамики.
Лекция 16. Информационные технологии в экологии. Экологические информационные системы.
1 6.1. Экологические информационные системы
1. Какова область значения для числовых характеристик?
Лекция 17. Использование информационных технологий для решения задач экологии.
Критические значения коэффициента корреляции rk;α
2.1. Подобие физических явлений и его признаки
2.4. Применение методов подобия в математическом
11.3. Численные методы решения дифференциальных уравнений
11.3.2. Процесс численного решения
11.3.4. Модифицированный метод Эйлера
11.3.6. Метод Рунге – Кутта для систем дифференциальных уравнений
11.3.7. Общая характеристика одношаговых методов
11.3.9. Методы прогноза и коррекции
11.3.10. Краткая характеристика методов прогноза и коррекции.
11.3.11. Выбор шага и погрешность решения.
11.4. Имитационное моделирование систем
11.4.1. Принципы имитационного моделирования
11.4.3. Динамическая модель исследуемого объекта
11.4.4. Построение имитационных моделей динамических систем
11.4.5. Преобразование передаточных функций звеньев в дифференциальные уравнения в форме Коши
11.4.6. Синтез имитационной модели на основе структурной схемы
11.5. Теоретические основы построения математических моделей систем
11.5.1. Компонентные и топологические уравнения
11.5.2. Компонентные и топологические уравнения механической системы
11.5.3. Компонентные и топологические уравнения электрической системы
11.5.4. Компонентные и топологические уравнения гидравлической системы
11.5.5. Компонентные и топологические уравнения тепловой системы
11.6.1. Сущность метода электроаналогий.
11.6.2. Электромеханические аналогии
11.6.3. Построение имитационных моделей методом электроаналогий
11.6.4. Плоское прямолинейное движение звеньев
11.6.5. Электрогидравлические аналогии
то можно записать S = (Y — XB)T(Y — XB) (индекс «т» означает транспонирование).
Исходя
из
условий
минимизации
![]() ,
откуда
(XTX)B
=
XTY.
,
откуда
(XTX)B
=
XTY.
Следовательно, оценка МНК есть такая, при которой коэффи- циенты уравнения регрессии равны В = (XTX)-1ХTУ (индекс "-1" означает обратную матрицу). Коэффициент детерминации (скорректированный) равен:
![]()
Оценка
меры
автокорреляции
случайной
величины,
![]() как
правило,
производится с
помощью
статистики
Дарбина-Уот-
сона
как
правило,
производится с
помощью
статистики
Дарбина-Уот-
сона
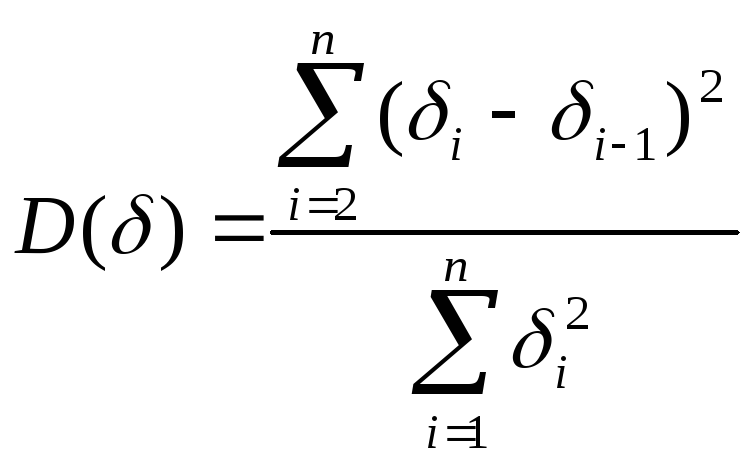
При значении D(δ), близком к двум, говорят, что автокорреляция отсутствует (что желательно).
Пример. В результате эксперимента зафиксированы пары значений (хi,уi), приведенных в табл. 5.2: Построить уравнение регрессии вида у = b0+b1х
Таблица 5.2
Результаты эксперимента
|
xi |
1 |
3 |
2 |
5 |
2 |
5 |
6 |
2 |
3 |
6 |
4 |
1 |
3 |
4 |
6 |
5 |
1 |
4 |
|
yi |
3 |
5 |
3 |
4 |
3 |
б |
7 |
2 |
3 |
8 |
6 |
2 |
4 |
4 |
8 |
6 |
1 |
5 |
Решение. Для вычисления коэффициентов уравнения регрессии составляем статистическую табл. 5.3.
По вычисленным суммам определяем:
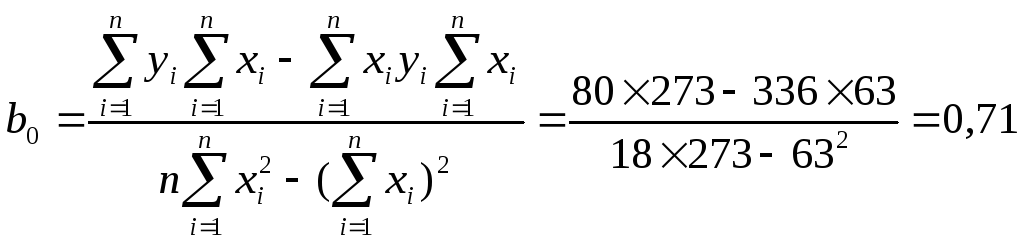
![]()
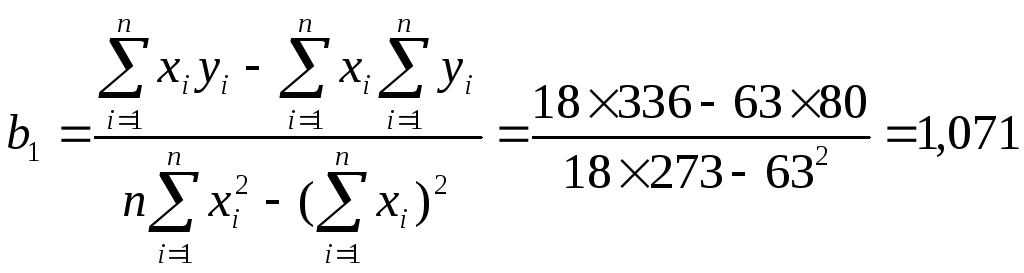
Тогда
уравнение
регрессии
будет
иметь
вид
![]() .
.
Таблица 5.3
Статистическая таблица эксперимента
|
Номер опыта |
Значения Xi |
Значения Уi. |
ХiYi |
Xi2 |
Yi2 |
|
1 |
1 |
3 |
3 |
1 |
9 |
|
2 |
1 |
2 |
2 |
1 |
4 |
|
3 |
1 |
1 |
1 |
1 |
1 |
|
4 |
2 |
2 |
4 |
4 |
4 |
|
5 |
2 |
3 |
6 |
4 |
9 |
|
6 |
2 |
3 |
6 |
4 |
9 |
|
7 |
3 |
4 |
12 |
9 |
16 |
|
8 |
3 |
3 |
9 |
9 |
9 |
|
9 |
3 |
5 |
15 |
9 |
25 |
|
10 |
4 |
4 |
16 |
16 |
16 |
|
11 |
4 |
5 |
20 |
16 |
25 |
|
12 |
4 |
6 |
24 |
16 |
36 |
|
13 |
5 |
4 |
20 |
25 |
16 |
|
14 |
5 |
6 |
30 |
25 |
36 |
|
15 |
5 |
6 |
30 |
25 |
36 |
|
16 |
6 |
7 |
42 |
36 |
49 |
|
17 |
6 |
8 |
48 |
36 |
64 |
|
18 |
6 |
8 |
48 |
36 |
64 |
|
|
63 |
80 |
336 |
273 |
428 |
Определяем коэффициент корреляции:
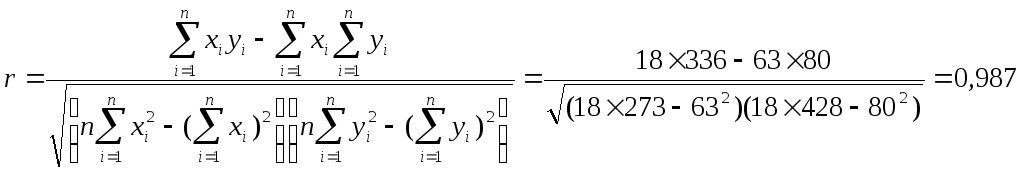 ,
,
отсюда следует, что Y и Х тесно связаны друг с другом, так как коэффициент корреляции близок к единице.
При нелинейной форме связи могут быть использованы два подхода:
• первый — когда нелинейная форма связи представляется в виде линеаризованной функции;
• второй — когда используется итерационный нелинейный метод наименьших квадратов.
В первом случае исследователь сначала выбирает форму нелинейной связи, затем её линеаризует, преобразуя члены уравнения регрессии, например, как это показано в табл. 5.4.
Таблица 5.4.
Пример преобразования членов уравнения регрессии
|
Функция |
Линеаризующие преобразования |
|||
|
Преобразование переменных |
Преобразование коэффициентов |
|||
|
Y1 |
Х1 |
|
|
|
|
y = b0+b1/х |
y |
1/х |
b0 |
b1 |
|
y= 1/(b0+b1x) |
1/y |
х |
b0 |
b1 |
|
y= x/(b0+b1x) |
х/у |
х |
b0 |
b1 |
|
у
=b0 |
lny |
х |
lnb0 |
lnb1, |
|
y =b0ebx |
lny |
х |
lnb0 |
b1 |
|
y=1/(b0+b1e-x) |
1/у |
e-x |
b0 |
b1 |
|
у = b0xb |
lny |
lnx |
lnb0 |
b1 |
|
у =b0+b1lпх |
y |
lnx |
b0 |
b1, |
|
у = b0/(b1+х) |
1/y |
х |
b1/b0 |
1/ b1 |
|
у = b0х/(b1+х) |
1/у |
1/х |
b1/b0 |
1/b1 |
|
y = b0+b1xn |
y |
xn |
b0 |
b1 |
Затем используется метод МНК для линеаризованного уравнения, откуда определяются коэффициенты уравнения регрессии. По- лученное уравнение регрессии затем вновь преобразуется в нелинейную форму.
Пример. В результате многолетних исследований зависимости толщины слоя ила после разлива на пойменных лугах от толщины снежного покрова получены данные, показанные в табл. 5.5.
Таблица 5.5
|
Толщина |
|
|
|
|
|
|
|
|
снежного покрова Х, см |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
слоя ила Y, см |
0,5 |
1,0 |
1,4 |
1,7 |
1.8 |
1,9 |
2,0 |
Требуется найти зависимость между толщиной снежного покрова и толщиной слоя ила.
Р е ш е н и е. Предполагаем зависимость между Х и Y вида у = abx. Линеаризуем уравнение, при у' = lny; х' = х; а' = lnа и b' = lnb, тогда у' = а' +xb'. Составляем статистическую таблицу.
Составляем систему нормальных уравнений МНК:
na' + b' ∑ х = у' 7a' + b'28 = 0,9106
или
а'х+ ∑х2 = ху' 28a'+ 140b' = 6,1152.
Таблица 5.6
Вычисление данных для линеаризации уравнения регрессии
|
Х |
Y |
lny |
xlny |
x2 |
|
1 |
0,5 |
- 0.3010 |
- 0,3010 |
1 |
|
2 |
1,0 |
0 |
0 |
4 |
|
3 |
1,4 |
0,1461 |
0,4383 |
9 |
|
4 |
1,7 |
0,2304 |
0,9216 |
16 |
|
5 |
1,8 |
0,2553 |
1,2765 |
25 |
|
6 |
1,9 |
0,2788 |
1,6728 |
36 |
|
7 |
2.0 |
0,3010 |
2,1070 |
49 |
|
∑=28 |
10,3 |
0,9106 |
6,1152 |
140 |
После преобразований получим: а = 0,6; b = 1,226. Следовательно, уравнение регрессии для зависимости толщины слоя ила от толщины снежного покрова будет иметь вид:
![]() =
=
![]()
В табл. 5.7 даны нормальные уравнения МНК для некоторых функций.
Таблица 5.7
Нормальные уравнения мнк для некоторых функций
|
Функции |
Нормальные уравнения |
|
y = a+bx |
an + b∑x =∑у; a∑ + b∑х2 = ∑ху |
|
у = аЬxсx2 |
nlga + lgb∑x + lgс∑х2 = ∑lgy lga∑x + lgb∑x2 + lgc∑x3 = ∑lgxlgy; lg∑x2+lg∑x3+lg∑4 =∑х2lgy |
|
lgy = a+ bx |
an + b∑ = ∑lgy; a∑х + b∑x2 = ∑xlgy |
|
y = а+ bx+ сх2 |
na + b∑х + с∑х2 =∑у а∑х + b∑x2 + с∑х3 = ∑ху a∑x2+ b∑x3 + с∑x4 =∑x2у |
|
у =аbx |
nlga+ lgb∑x = ∑lgy lga∑x + lgb∑x2 = ∑lg xlg y |
|
y = a+b - lgx |
an+ b∑lgx = ∑у a∑lgх + b∑(lnх)2= ∑lgxlgy |