ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 31.03.2024
Просмотров: 1138
Скачиваний: 0
СОДЕРЖАНИЕ
Математическое моделирование элементов сложных экологических систем
Лекция 1. Введение в моделирование. Исторический экскурс.
1. Основы моделирования в экологии 1.1. Общие принципы построения моделей в экологии
2.2. Этапы построения математической модели
1.4. Элементы теории подобия, применяемые в моделировании
3.2.2. Выборочный метод в экологометрике.
Зависимость числа интервалов от объема выборки
Статистический ряд по интервалам
Лекция 4. Статистические оценки параметров распределения случайных величин по выборкам
4.4. Статистические оценки гипотез об экологических моделях
Выборка из генеральной совокупности
Статистическая таблица эксперимента
Пример преобразования членов уравнения регрессии
Вычисление данных для линеаризации уравнения регрессии
Нормальные уравнения мнк для некоторых функций
Статистическое оценивание уравнения регрессии и парной корреляции.
Обработка результатов наблюдений
Рекомендации по выбору вида функции
3.4. Динамические статистические модели
Данные по объему сброса качественных сточных вод
Данные по объему сброса сточных вод за 5-летие
Пример расчета 5-летних средних
Расчетные значения для определения уравнения динамики
Ряд динамики для определения сезонных колебаний
Эксперименталъный материал исследования
8.1. Анализ влияния отдельных факторов в экологической модели.
Лекция 9. Методы оптимизации. Метод Лагранжа
Лекция 10. Метод линейного программирования.
Лекция 11. Функциональные модели.
Лекция 12. Модели процессов содержащие обыкновенные дифференциальные уравнения.
Численные ошибки использованных для вычисления данных
Лекция 13. Статистические модели динамики.
Лекция 16. Информационные технологии в экологии. Экологические информационные системы.
1 6.1. Экологические информационные системы
1. Какова область значения для числовых характеристик?
Лекция 17. Использование информационных технологий для решения задач экологии.
Критические значения коэффициента корреляции rk;α
2.1. Подобие физических явлений и его признаки
2.4. Применение методов подобия в математическом
11.3. Численные методы решения дифференциальных уравнений
11.3.2. Процесс численного решения
11.3.4. Модифицированный метод Эйлера
11.3.6. Метод Рунге – Кутта для систем дифференциальных уравнений
11.3.7. Общая характеристика одношаговых методов
11.3.9. Методы прогноза и коррекции
11.3.10. Краткая характеристика методов прогноза и коррекции.
11.3.11. Выбор шага и погрешность решения.
11.4. Имитационное моделирование систем
11.4.1. Принципы имитационного моделирования
11.4.3. Динамическая модель исследуемого объекта
11.4.4. Построение имитационных моделей динамических систем
11.4.5. Преобразование передаточных функций звеньев в дифференциальные уравнения в форме Коши
11.4.6. Синтез имитационной модели на основе структурной схемы
11.5. Теоретические основы построения математических моделей систем
11.5.1. Компонентные и топологические уравнения
11.5.2. Компонентные и топологические уравнения механической системы
11.5.3. Компонентные и топологические уравнения электрической системы
11.5.4. Компонентные и топологические уравнения гидравлической системы
11.5.5. Компонентные и топологические уравнения тепловой системы
11.6.1. Сущность метода электроаналогий.
11.6.2. Электромеханические аналогии
11.6.3. Построение имитационных моделей методом электроаналогий
11.6.4. Плоское прямолинейное движение звеньев
11.6.5. Электрогидравлические аналогии
Сезонность можно понимать как внутригодовую динамику вообще. Моделью периодически изменяющихся уровней служит ряд Фурье, аналитическое выражение которого применительно к динамике имеет вид
![]()
В этом уравнении величина k определяет номер гармоники ряда Фурье и может быть взята с необходимой степенью точности (чаще всего от 1 до 4). Параметры уравнения определяются методом МНК по формулам
![]()
![]()
![]()
Для изучения специфического периодического явления сезонности берем n=12 (число месяцев в году), а ряд динамики можно записать в виде, показанном в табл. 6.9.
Таблица 6.9
Ряд динамики для определения сезонных колебаний
|
0 |
π/6 |
π /3 |
π /2 |
2π/3 |
5π/6 |
π |
7π/6 |
4π/3 |
3π/2 |
5π/3 |
11π/6 |
|
y0 |
y1 |
y2 |
y3 |
y4 |
y5 |
y6 |
y7 |
y8 |
y9 |
y10 |
y11 |
При вычислениях принимается во внимание, что в четырех квадратах от 0 до 2π косинусы и синусы четыре раза принимают одни и те же значения: 0; 0,5; 0,866 и 1, взятые со знаком минус или плюс.
Пример. Рассмотрим модель сезонности для данных, приведенных в табл. 6.10.
Таблица 6.10
Данные о периодически изменяющихся уровнях по месяцам
|
Месяц |
t |
у |
Cos(t) |
Sin(t) |
yсоs(t) |
ysin(t) |
yt |
|
1 |
0 |
39,8 |
1,000 |
0,000 |
39,80 |
0,00 |
44,17 |
|
2 |
π/6 |
62,2 |
0,866 |
0,500 |
53,86 |
31,10 |
93,70 |
|
3 |
π /3 |
125,5 |
0,500 |
0,866 |
62,95 |
109,03 |
152,13 |
|
4 |
π /2 |
256,2 |
0,000 |
1,000 |
0,00 |
256,20 |
205,81 |
|
5 |
2π/3 |
271,1 |
-0,500 |
0,866 |
138,05 |
239,10 |
234,88 |
|
6 |
5π/6 |
255,7 |
-0866 |
0500 |
-221,44 |
127,85 |
237,04 |
|
7 |
π |
177,6 |
-1,000 |
0,000 |
-177,60 |
0,00 |
168,31 |
|
8 |
7π/6 |
144,0 |
- 0866 |
- 0,000 |
-124,70 |
122,00 |
160,16 |
|
9 |
4π/3 |
86,7 |
-0,500 t |
-0,866 |
- 46,35 |
-75,08 |
129,87 |
|
10 |
3π/2 |
52,8 |
0,000 |
-1,000 |
0,000 |
52,80 |
88,49 |
|
11 |
5π/3 |
38,3 |
0,500 |
- 0,866 |
19,15 |
-33,17 |
18,97 |
|
12 |
11π/6 |
37,9 |
- 0,866 |
- 0,500 |
32,82 |
-18,95 |
16,82 |
|
Сумма |
- |
1553,2 |
- |
- |
- 496,56 |
461,28 |
1552,9 |
Р е ш е н и е. Вычисляем cos(t), sin(t), у∙cos(t), у∙sin(t) и определяем
![]()
![]()
![]()
![]()
Тогда уравнение. сезонной модели будет иметь вид
![]()
Индексом сезонности называется отношение средней из фактических уровней одноименных месяцев к средней из выровненных данных по тем же месяцам
![]()
![]()
Следовательно, величина iсез различна для каждого месяца и зависит от способа выравнивания, которое может быть проведено либо применением 12-месячной скользящей средней, либо аналитическим выравниванием.
Показателем силы колеблемости динамического ряда из-за се- зонного характера процесса служит среднее квадратическое отклонение индексов сезонности (выражается в процентах) от 100 %
![]()
Сравнение
средних
квадратических
отклонений,
вычисленных
за
два
периода,
показывают сдвиги
в
сезонности.
Если
величина
![]() уменьшается,
то
сезонный
характер исследуемого
явления
идет
на
убыль.
уменьшается,
то
сезонный
характер исследуемого
явления
идет
на
убыль.
Изучение глубины сезонных колебаний возможно и путем определения отношений отклонения фактических уровней от выровненных к теоретическим отклонениям, принятым за «норму».
Некоторые способы измерения размаха сезонной волны основаны на изучении не абсолютных отклонений фактических данных от выровненных, а отклонений с учетом знака.
назад
Лекция 7. Многофакторные эколого-математические модели. Анализ влияния отдельных факторов в экологической модели.
В практике часто возникают ситуации, когда функция отклика (цели) У зависит не от одного, а от многих факторов. Установление формы связи в этих случаях начинают, как правило, с рассмотрения линейной регрессии вида
![]()
В этом случае результаты наблюдений должны быть представлены
уравнениями, полученными в каждом из и опытов:
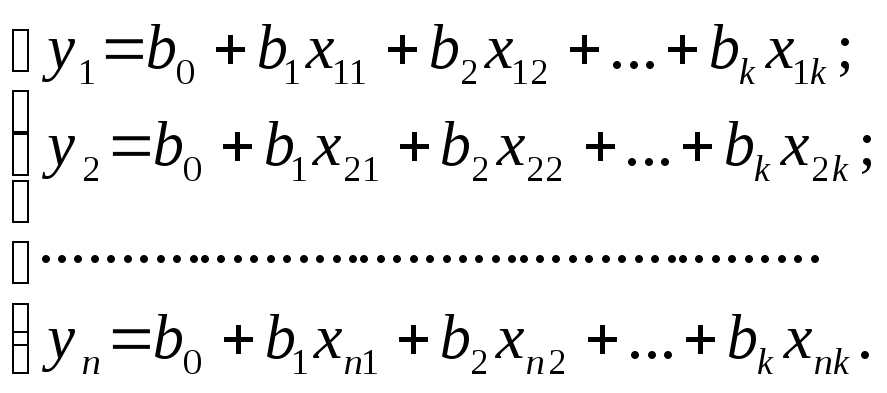
или в виде матрицы результатов наблюдений

где n — количество опытов; k — количество факторов.
Для решения систем уравнений необходимо, чтобы количество опытов было не менее (k+1), т.е. n > k+l.
Задачей множественного регрессионного анализа является пост- роение такого уравнения прямой в k-мерном пространстве, откло- нения результатов наблюдений хij от которой были бы минималь- ными. Используя для этого метод наименьших квадратов, получаем систему нормальных уравнений
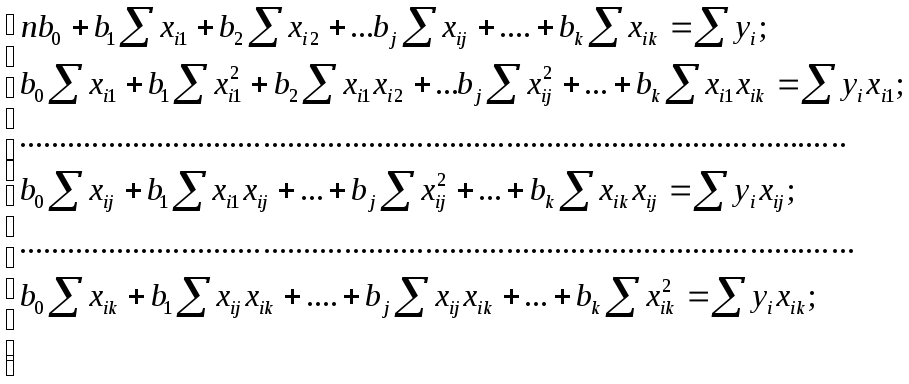
В матричном виде
![]() ,
,
где В — вектор-столбец коэффициентов уравнения регрессии;
Х — матрица значений факторов; Y — вектор-столбец функций отклика; ХT — транспонированная матрица Х Они соответственно равны:
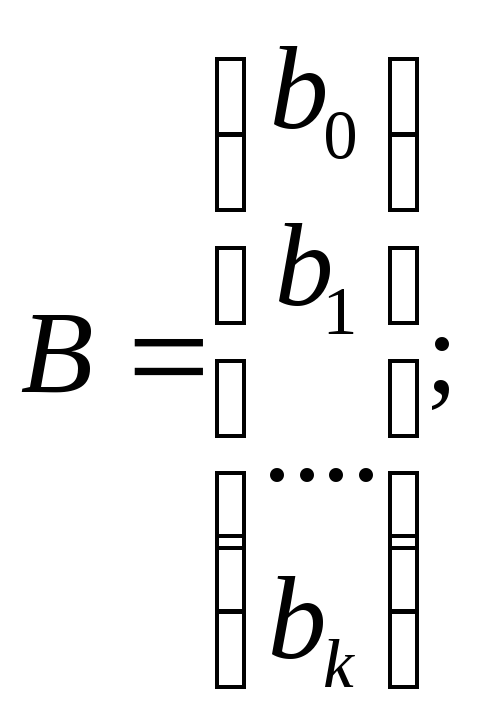
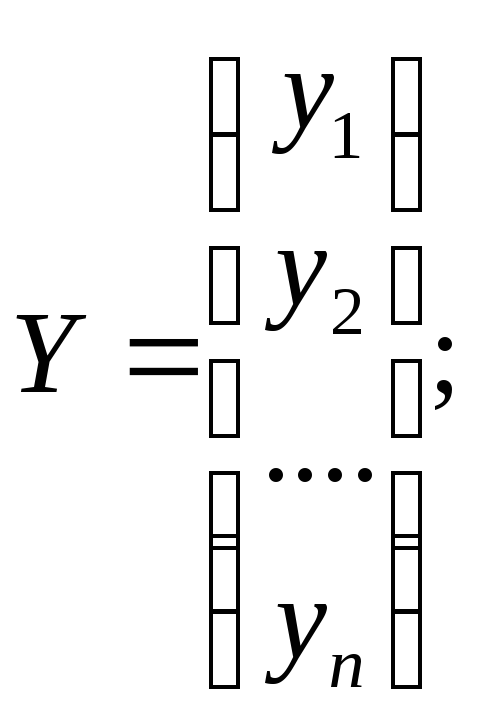
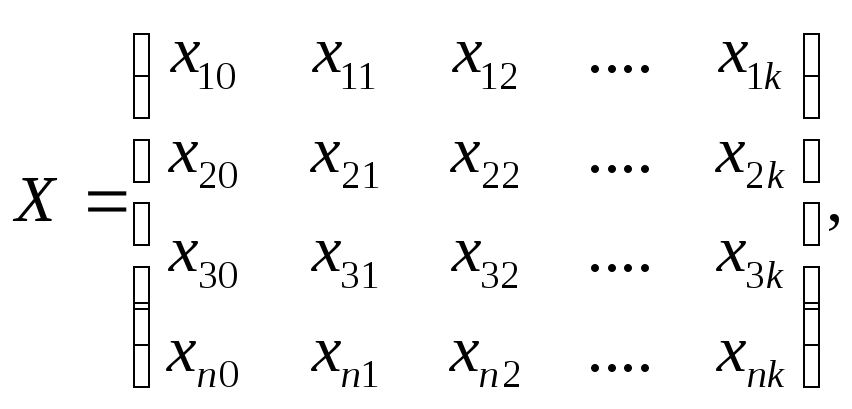
при хj0 = 1, j =1,n;
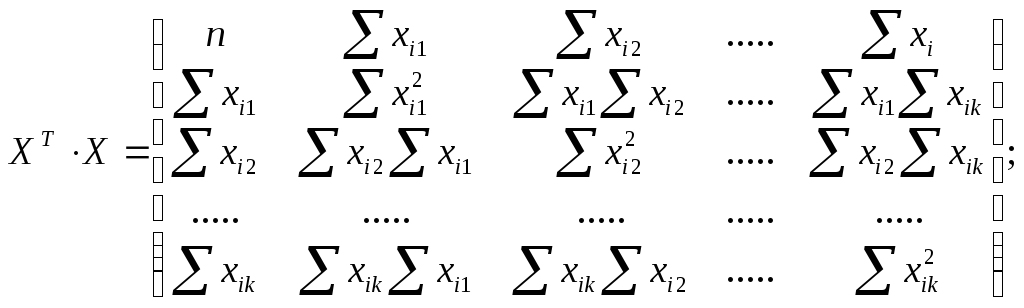
Умножая правую и левую части уравнения на обратную матри- цу (ХT∙Х)-1, при (ХT∙Х)-1∙(ХT∙Х)-1= Е = 1 получим:
(ХT∙Х)-1(ХT∙Х)В= (ХT∙Х)-1(ХT∙Y).
Откуда В=(ХT∙Х)-1(ХT∙Y). Каждый коэффициент уравнения регрессии вычисляется по формуле
![]()
где сij — элементы обратной матрицы (ХT∙Х)-1.
Пример. В результате проведенных исследований влияния мощ- ности гумусового слоя почвы (Х1) и количества внесенного слож- ного состава минерального удобрения (Х2) на урожайность зерно- вой культуры (Y) получены уравнения:
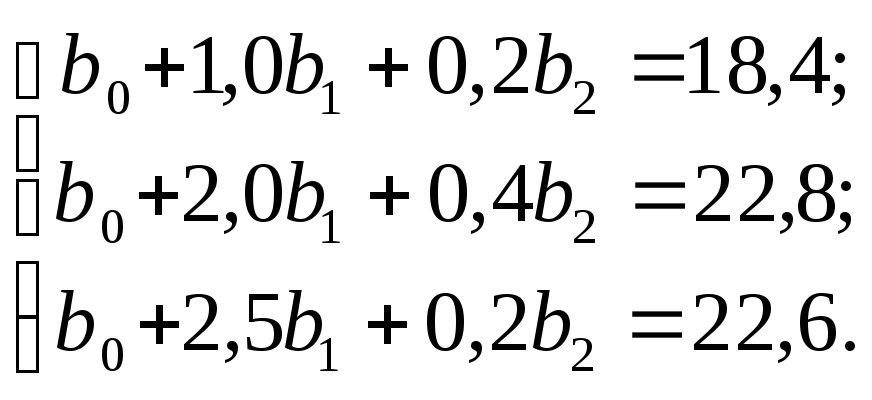
Установить форму связи урожайности е факторами х1 и х2 в виде линейного уравнения регрессии.
Р е ш е н и е. Представляем результаты опытов в виде матриц:
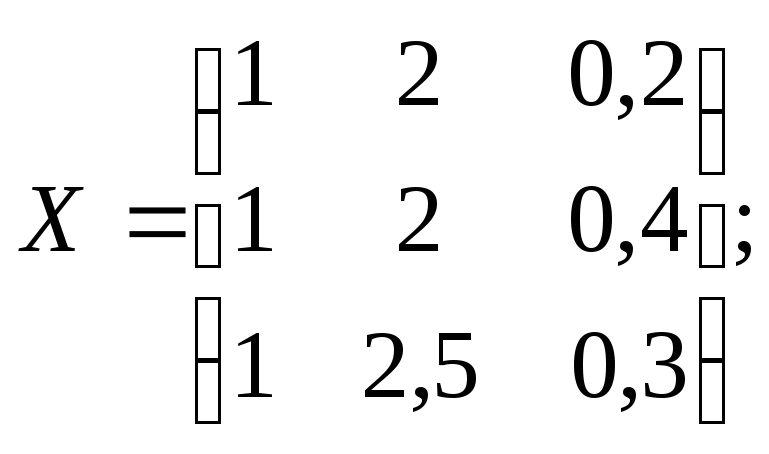
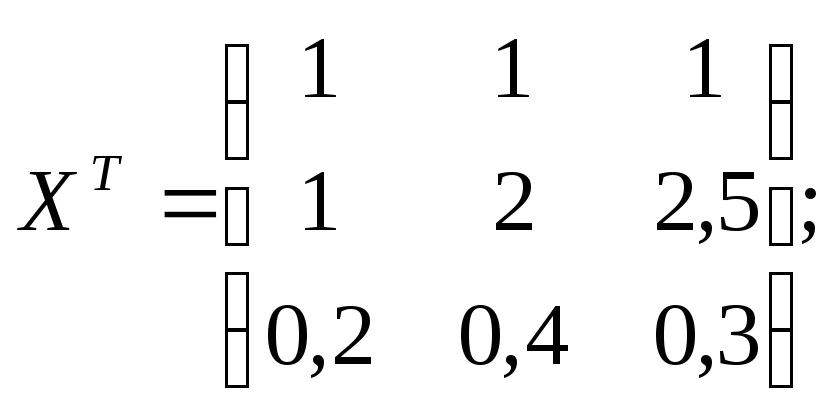
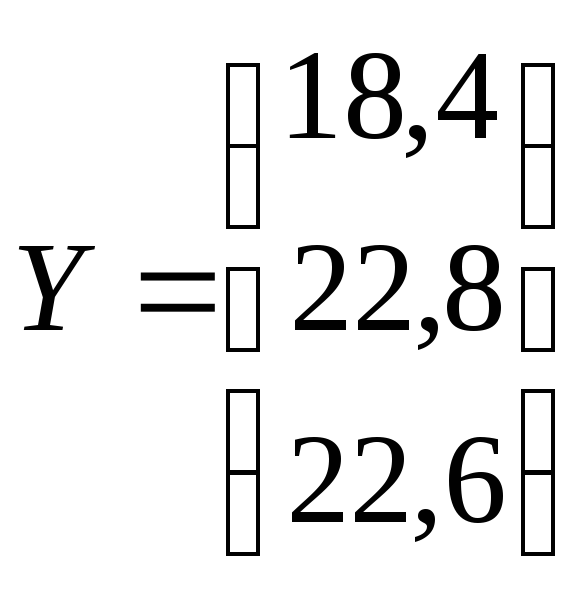

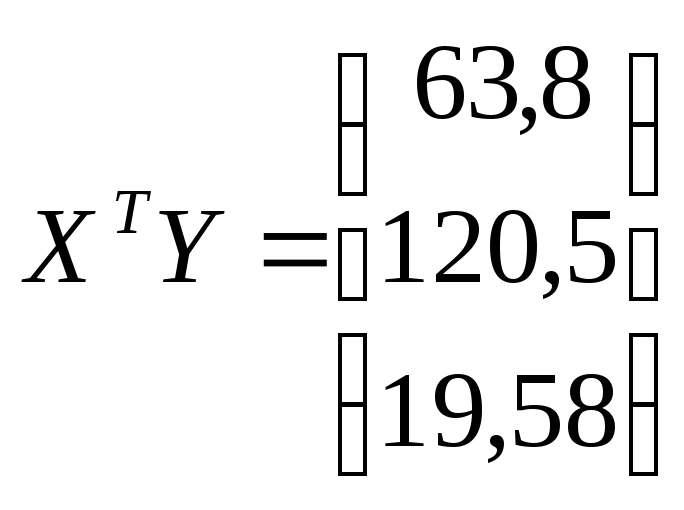
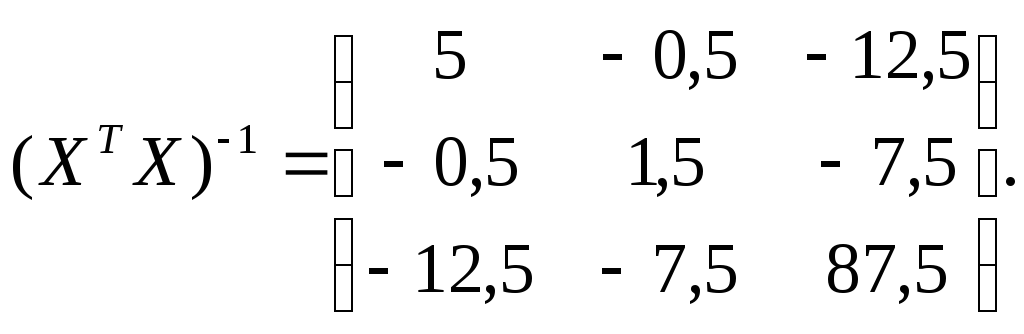
Определяем коэффициенты уравнения регрессии
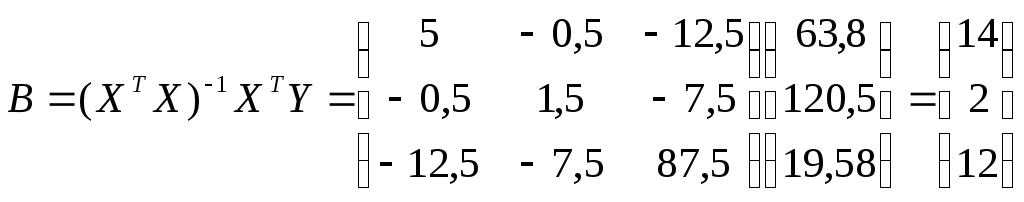
Отсюда b0 = 14, b1 = 2, b2 = 12 и уравнение регрессии имеет вид
![]() =14+2х1
+12х2.
=14+2х1
+12х2.
Для проверки значимости уравнения регрессии необходимо при заданных значениях (х1,х2) провести несколько экспериментов, чтобы для данного значения (х1,х2) получить некоторое среднее значение функции у. В этом случае экспериментальный материал представляется, например, в виде табл. 7.1.
Таблица 7.1
Эксперименталъный материал исследования
|
№ п.п. |
Уровни факторов |
Значение функции y при паралельных опытах |
Опытное среднее значение |
|||
|
x1 |
x2 |
y1 |
y2 |
y3 |
yi |
|
|
1 |
1,0 |
0,2 |
18,2 |
18,6 |
18,7 |
18,5 |
|
2 |
2,0 |
0,4 |
21,6 |
23,4 |
23,7 |
22,9 |
|
3 |
2,5 |
0,3 |
22,0 |
23,0 |
22,5 |
22,5 |