Файл: Математическое моделирование в экологии.doc

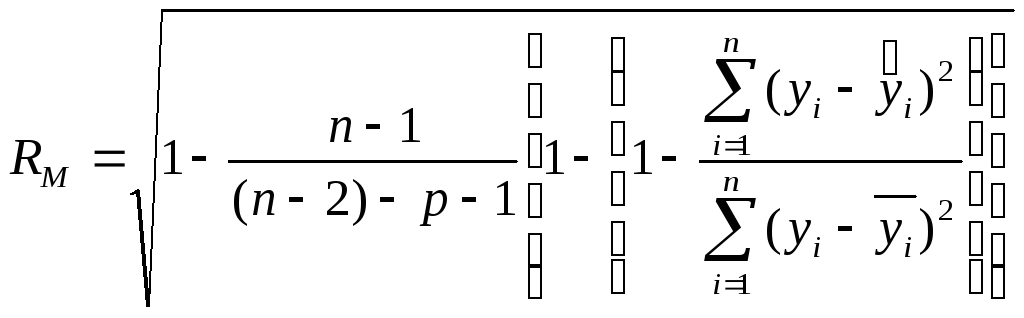
или

где D — определитель корреляционной матрицы.

Если R_M возвести в квадрат, то величина R²_M называется множественным коэффициентом детерминации и показывает, какая часть дисперсии функции отклика объясняется вариацией линейной комбинации выбранных факторов.

При (р<k), х₁, х₂, ...., х_p значимость R_M можно проверить: а) по t-критерию

б) по F-критерию

где k₁=n - р - 1 и k₂ = р.

Пример. Для предыдущего примера, использовавшего данные табл. 7.2, вычислить коэффициенты корреляции.

Р е ш е н и е. С целью облегчения вычислений результаты работы сведем в табл. 7.3.

Таблица 7.3. Результаты вычислений исследования

Вычислим вспомогательные числа:

Вычисляем коэффициент, определяющий степень связи между функцией Y и фактором х₁

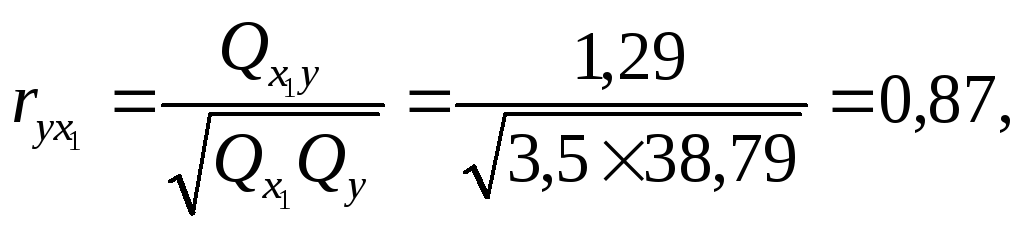
Определяем тесноту связи между факторами Y и х₂

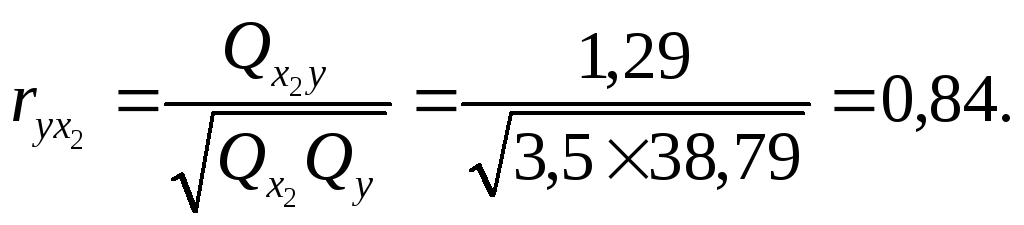
Определяем тесноту связи между факторами x₁ и x₂

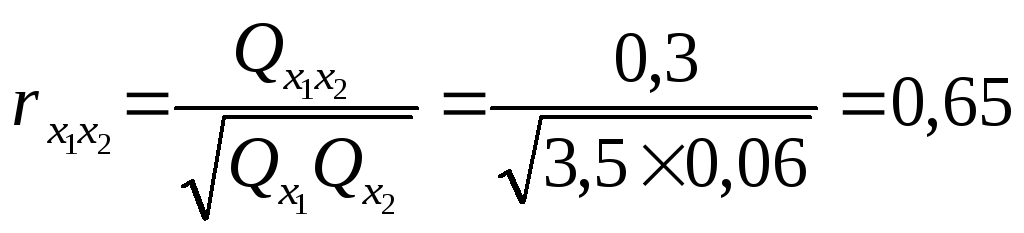
Где

Составляем корреляционную матрицу

и определяем частные коэффициенты корреляции

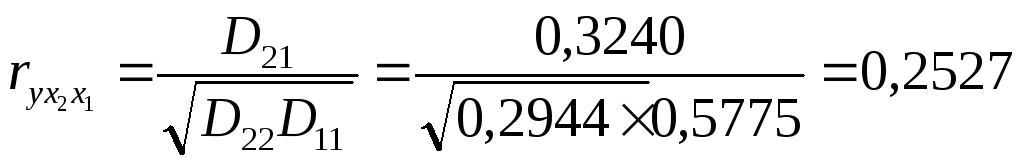
где

вычисляем коэффициент множественной корреляции

где

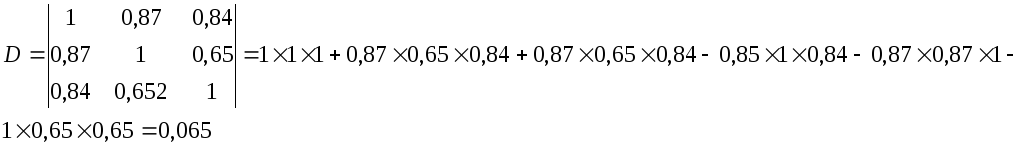Величина множественного коэффициента детерминации равна:

.

Отсюда можно сделать вывод, что 78,7% дисперсии функции отклика объясняется вариацией линейной комбинации факто- ров х₁ и х₂.

Множественный нелинейный регрессионный анализ. При переходе от линейной к нелинейной модели для функции отклика Y анализ результатов статистических наблюдений начинают с модели так называемой квадратичной формы

Данное уравнение линеаризуется заменой переменных . По полученному уравнению регрессии представляют опытные данные и определяют коэффициенты b₀, b₁, b₂, b₁₁, ....

Затем производят все вычисления аналогично сделанным для случая линейного множественного корреляционно-регрессионного анализа. Если квадратичная форма неадекватна статистическому материалу (результатам эксперимента), то степень уравнения повышается. В практике предельным уравнением бывает кубическая форма. При переходе к высшей степени уравнение регрес-сии линеаризуется заменой переменных.

Кроме полиномиальной модели в нелинейном регрессионном анализе используются:

а) мультипликативные модели

,

логарифмируя которые, преобразуем в линейные модели

,

с заменой переменных: у' = lny; ;

б) экспоненциальные модели

у = ехр(b₀ + b₁x₁ + b₂х₂ + ... + b_kх_k), логарифмируя которые, получим

lnу =b₀+b₁х₁ +b₂x₂+...+b_kх_k;

в) обратные модели

,

можно привести к виду

Для определения корреляционной связи в нелинейных моделях используют множественное корреляционное отношение, при этом для вычисления остаточ-ной дисперсии используется нелинейная форма функции отклика у.

При поиске наилучшей модели функции отклика можно использовать раз-личные нелинейные функции, лучшей из них будет та, которая будет иметь наименьшую величину остаточной дисперсии .

При построении регрессивной модели для целевой функции Y на начальном этапе следует учитывать как можно большее число факторов, влияющих на изменение Y. В этом случае получаются достаточно сложные модели, особенно при использовании нелинейных форм. Часто эти модели можно значительно упростить, если в них выявить те факторы, которые незначительно влияют на функцию отклика или один из двух, имеющих сильную корреляцию между собой, и эти факторы не включать в уравнение регрессии.

Для анализа регрессионных моделей используется несколько методов: метод всех регрессий; метод исключения переменных; метод включения переменных; анализ остатков и др.

При применении метода всех регрессий функцию отклика представляют в виде комбинаций зависимостей, в которых меняют число факторов.

Так в уравнении регрессии

,

можно записать функцию отклика в различных комбинациях

и т.д.

Для каждого уравнения вычисляются коэффициенты регрессии и определяется остаточная дисперсия понаименьшему значению которой и выбирается лучшее уравнение. Применение этого метода связано с трудоемкими вычислениями.

При применении метода исключения переменных уравнение регрессии желательно представить сразу в полной квадратичной или кубичной форме с предварительным вычислением коэффициентов регрессии и корреляции и проверкой линейности модели по F-кри- терию. Исключение начинают с фактора, имеющего наименьший t-- критерий. На каждом этапе после исключения каждого фактора для нового уравнения регрессии вычисляется множественный коэффициент корреляции, остаточная дисперсия и F-критерий. Для прекращения исключения факторов следует следить за изменением остаточной дисперсии. Как только она начнет увеличиваться — исключение факторов следует прекратить. Используется также метод контроля значений t-критерия. Для исключения следующего фактора мы сравниваем его значение (t) с t-критерием предыдущего исключенного фактора и, если они отличаются незначительно, то фактор исключается. Если же различия t-критериев значительны, то исключение факторов прекращают.

Метод включения переменных состоит в том, что на первом этапе выбирают фактор, у которого r_yx наибольший, и строят линейное уравнение

у = f(x_i).

Затем вычисляют частный коэффициент корреляции. После это- го берут следующую величину х_i+1 и находят второе уравнение

у = f(x_i, x_i+1)

и вычисляют частный коэффициент корреляции и т.д. Этот метод используется совместно с анализом остатков.

Метод анализа остатков состоит в том, что анализируется разница между значением функции у_i и предсказываемым ее значением (уравнением регрес-сии). Определяя остатки

е_i = у_i -, i=,

мы проверяем их среднее значение, которое должно быть равно нулю, т.е.

.

Если это условие не соблюдается, то в уравнение вносят дополнительные члены или же проводятся другие преобразования исходных данных.

назад

Лекция 8.

(Самостоятельно – Гринин А.С., Орехов Н.А., Новиков В.Н. Глава 3 §3.6.) Некоторые особенности применения экспериментально-статистических методов в экологии. Проверка статистических гипотез при планировании экспериментов.