Файл: Математическое моделирование в экологии.doc

• идентифицируемость — каждый элемент системы может быть отделен от других составляющих;

• стабилизация — система осуществляет восстановление своих элементов за счет их регулирования;

• наблюдаемость — все без исключения входы и выходы системы либо контролируемы наблюдателем, либо, по крайней мере, наблюдаемы;

• неопределенность — наблюдатель одновременно не может фиксировать свойства и отношения элементов системы; именно с целью их выявления он осуществляет системное исследование;

• нетождественность отображения — знаковая система наблюдателя отлична от знаковой системы проявления свойств объектов и их отношений; потеря информации при этом определяет нетожде- ственность системы исследуемому объекту;

• адаптация — система сохраняет состояние подвижного равновесия и устойчивость к возмущающим воздействиям, которым она постоянно подвергается путем перестройки внутренней структуры и функций отдельных элементов. Она меняет свои рабочие характеристики в соответствии с изменяющимися внешними условиями или входным сигналом таким образом, чтобы постоянно улучшать показатель качества. Система обеспечивает длительное и устойчивое функционирование и развитие путем эволюции своих элементов, своей структуры и организации.

Любая система в процессе перехода от качественных описаний к количественным, в некоторый момент достигает такого уровня, когда для фиксации связей, в процессе изучения с помощью теории и эксперимента, наиболее действенным оказывается использование математического аппарата. Если рассматривать экологическую практику как сочетание информации, традиций и инструкций, то развитие познаний об экологических системах можно условно представить в виде схемы, приведенной на рис. 1.2.

Экологические системы, как правило, можно рассматривать как иерархические, для которых характерны три важных свойства:

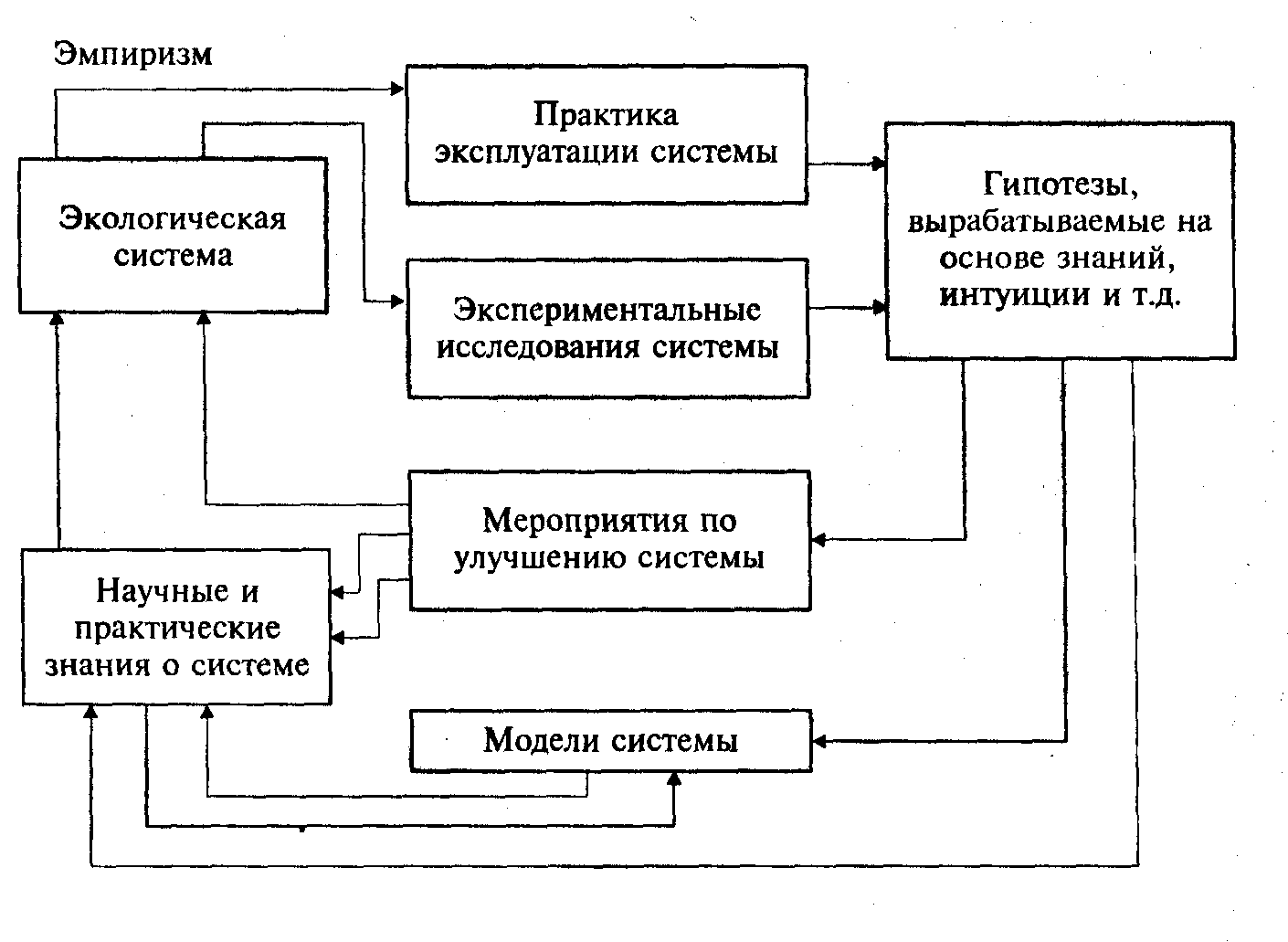
Рис. 1.2. Схема развития познаний об экологической системе

1) каждый уровень иерархии имеет свой собственный язык, свою систему концепций или принципов. К примеру, понятия «озоновая дыра», «мировая атмосфера» и другие лишены смысла на уровне исследования небольшого участка леса;

2) на каждом уровне иерархии происходит обобщение свойств объектов более низкого уровня;

3) взаимосвязи между уровнями не симметричны.

Для нормального функционирования объектов высшего уровня необходимо, чтобы успешно действовали объекты более низкого уровня, но не наоборот.

Обычно решающим оказывается то обстоятельство, что среди отдельных элементов рассматриваемой системы лишь немногие бывают плохо изученными. Если элементы определены плохо, то при исследовании реакций системы в целом трудно установить, какие из элементов приводят к изменению значений искомых функций. Чем больше модель, тем осторожнее следует к ней относиться. В особенности это свойственно оценке сообщения между уровнями знаний и теми результатами, которые предполагается получить с помощью моделирования. Модель, которая была бы просто большой, построить легко. Однако при весьма высокой стоимости ценность ее может оказаться сомнительной. Построить эффективную модель - значит найти такое ее описание, дающее ответ на конкретно поставленный вопрос. Это требует определенных навыков, и даже искусства, которое называют искусством разрешимого. Его главная цель — не искать решения, если для этого не достигнут определенный уровень знаний и нет соответствующей технической оснащенности.

При построении моделей можно выделить эмпирические и функциональные.

Главная задача эмпирических моделей — описать исследуемый объект, тогда как функциональное моделирование связано с попыткой дать объяснение опи-санному. Разработка эмпирической модели остается на одном уровне системы.

Разработка функциональной модели опирается на описание поведения системы в зависимости от подсистем более низ- кого уровня и тогда смежные уровни оказываются связанными посредством аналитико-синтетического процесса, опирающегося на соответствующие гипотезы или допущения. Любая функциональная модель, в конечном счете, уходит корнями в эмпиризм.

Всегда можно построить такую эмпирическую модель, которая была бы согласована с опытными данными лучше, чем функциональная. Это следует из того факта, что эмпирическая модель практически свободна от ограничений, в то время как возможности функциональной модели ограничиваются положен-ными в ее основу допущениями, даже если она содержит хорошо регулируемые пара- метры.

Модели систем можно также разделить на статические, динамические и стохастические:

• статическая модель — это математическая конструкция, в которую не включена переменная времени, используется тогда, когда система достаточно близка к равновесию;

• динамическая модель учитывает изменение состояния системы в зависимости от времени. В нее часто включаются элементы из статических моделей (статические и динамические модели относятся к классу детерминистских, главная особенность которых заключается в том, что любой прогноз они формируют в виде числа, а не в виде распределения вероятностей);

• стохастическая модель отличается тем, что в ней непременно присутствует одна или несколько случайных переменных, заданных соответствующими законами распределения. Это дает возможность не только оценивать среднее значение прогнозируемого параметра, но и его дисперсию. Чем больше неоп-ределенности в поведении системы, тем эффективнее оказывается стохастическая модель.

Модели систем играют значительную роль в понимании их функционирования и физической сущности, что заключается в следующем:

1. Гипотезы, выраженные математически, могут служить количественным описанием экологической проблемы и тем самым способствовать более углуб-ленному ее пониманию.

2. Требования, предъявляемые моделью к математической завершенности описания, позволяют построить определенную концептуальную основу и с ее помощью четко ограничить те области, где знание проблемы еще недостаточно, т.е. стимулирует возникновение новых идей и проведение экспериментальных исследований.

3. Математическая модель части подсказывает способ представления результатов научных исследований в форме, удобной для ис- следования на практике.

4. Благодаря модели может быть оценена количественно экономическая эффективность результатов научных исследований, что стимулирует оператив-ное их внедрение в производство.

5. Математическое моделирование, с помощью которого можно получить ответ на тот или иной специальный вопрос, а также сделать обоснованный выбор из ряда альтернативных стратегий, дает возможность сократить объем продолжительных и дорогостоящих экспериментальных работ, выполнение которых было бы необходимым при отсутствии соответствующих моделей.

6. При исследовании сложных многокомпонентных объектов модель позволяет объединить разрозненные знания, касающиеся отдельных частей такой системы, и выработать концепцию ее поведения как единого целого.

7. С помощью модели можно выбрать наиболее рациональную стратегию и тактику реализации исследовательских программ, обеспечивая необходимую детальность изучения специальных вопросов и кооперацию отдельных направлений исследования.

8. Математическая модель — мощное средство обобщения разнородных данных об объекте, позволяющее осуществлять как интерполяцию (восстано-вление недостающей информации о прошлом), так и экстраполяцию (прогно-зир-вание будущего поведения объекта).

9. Хорошо сконструированная модель позволяет наиболее полно использо-вать данные, получение которых, учитывая растущие требования к точности, обходится дорого.

10. Прогнозирующая способность модели может быть направлена на дости-жение самых разнообразных целей — планирования, оценки эффективности, прогнозирования и т.д.

назад

Лекция 2.

2.1. Элементы моделирования

Процесс моделирования связан с рядом процедур, например, таких как выбор целевой функции (функции отклика), переменных, параметров и т.д. Рассмотрим основные из них:

Выбор переменных. Различают переменные состояния, скорости (роста), факторов и др. Они в свою очередь подразделяются на вспомогательные и управляющие.

Переменные состояния определяют или помогают определить со- стояние системы в любой заданный момент времени (фазовые переменные). Типичным примером может служить объем выбросов и их содержание. Переменные должны поддаваться измерению и представлять интерес для исследователя. Так, если система задана с помо- щью n переменных состояния Х₁, Х₂, ..., Х_n, то они определяют един- ственным способом состояние системы в момент времени t. Проблема детерминированного моделирования состоит в построении дифференциальных уравнений, с помощью которых можно было бы прогнозировать значения всех переменных состояния системы в любой наперед заданный момент времени.

Переменные скорости (роста) — это характеристика, задающая процесс, который протекает в системе, в заданный момент времени. Эти процессы можно квалифицировать либо как преобразование, либо как перемещения.

Вспомогательные переменные способствуют более глубокому пониманию объекта и в отдельных случаях упрощают сопоставление результатов наблюдения, например темп роста выбросов в атмосферу

где П — объем выбросов;

dП — приращение объема выбросов за время dt.

Управляющие переменные — это не зависящие от времени количественные показатели и коэффициенты, включаемые в математические модели.

Под константой понимают численную величину, имеющую надежно и точно вычисленное значение, которое остается неизменным при варьировании условий эксперимента, а также в тех случаях, когда модель используется для проверки различных гипотез или для описания компонент системы.